Математическая модель ЦАП

ЦАП предназначен для преобразования числа представленного в виде двоичного кода на выходе ЦВМ, в эквивалентный аналоговый сигнал, представляющий собой электрическое напряжение (или ток). Процесс преобразования включает в себя два этапа: преобразование числового кода в дискретные моменты времени в квантованный по уровню импульсный сигнал, а затем преобразование импульсного сигнала в непрерывный кусочно-постоянный сигнал.

Квантование сигнала по уровню осуществляется в соответствии со статистической характеристикой ЦАП, изображенной на структурной схеме рис. 1 и представленной на рис. 3.

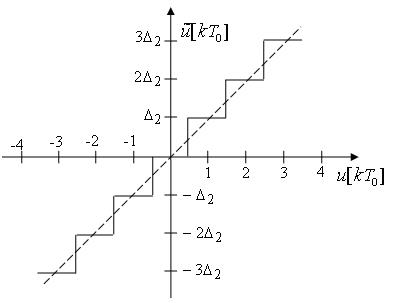
Рис. 3

Здесь для удобства по оси абсцисс отложен сигнал 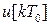с выхода ЦВМ в десятичной системе счисления, а по оси ординат – величина 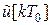, представляющая собой дискретное напряжение ЦАП. Единица младшего разряда выходной величины 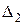зависит от количества разрядов 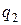преобразователя:

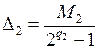, (4)

где 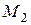– максимальное значение выходной величины ЦАП.

В соответствии с характеристикой рис. 3 справедлива зависимость

.

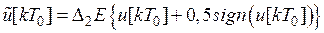Для осредненной характеристики ЦАП, показанной на рис. 3 пунктирной линией, коэффициент передачи равен

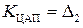. (5)

Тогда можно записать

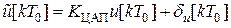, (6)

где 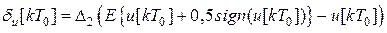– ошибка квантования по уровню, которая не превышает по модулю значения .

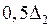На выходе ЦАП сигнал 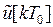экстраполируется кусочно-постоянным сигналом

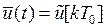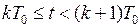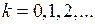при , , (7)

вид которого приведен на рис. 4.

На рис. 1 формирование сигнала (7) осуществляется с помощью идеального импульсного элемента, представленного ключом, и передаточной функции фиксатора нулевого порядка

.

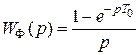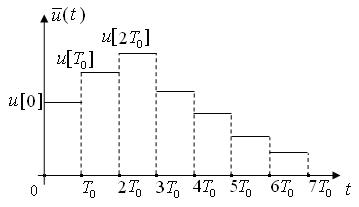
Рис. 4

Оценка точности ЦАС

Рассмотрим дискретную модель цифровой САУ с учетом квантования по уровню ЦАП, которую можно представить в виде

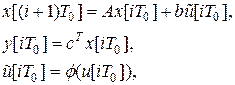(8)

где

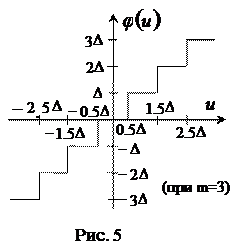
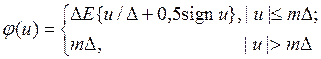(9)

статическая характеристика ЦАП (рис. 5) с ограниченным числом уровней 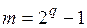, зависящим от числа двоичных разрядов 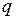преобразователя (без учета знакового разряда), при этом число 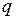определяется по заданному диапазону 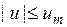и цене младшего разряда 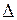: 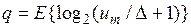. Здесь 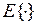– целая часть числа, заключенного в фигурные скобки.

Введем в рассмотрение шум квантования по уровню:

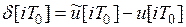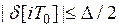, . (10)

Тогда систему (8) с учетом закона управления

,

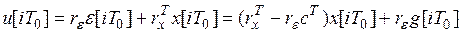где 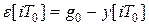, можно представить в виде

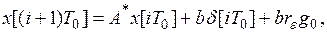(11)

где 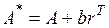– матрица замкнутой системы, у которой собственные значения 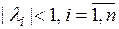и являются различными; .

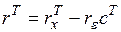Найдем установившийся режим системы (11) при отсутствии шума квантования по уровню, полагая 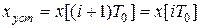при 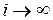. Из уравнения (11) после подстановки получим .

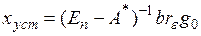Перепишем уравнение (11) в отклонении от установившегося режима полагая :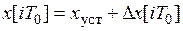

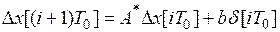. (12)

Найдем верхнюю оценку области изменения вектора 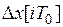в установившемся режиме при 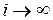. Для этого с помощью преобразования 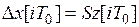, 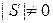приведем систему (12) к виду

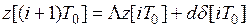, (13)

где 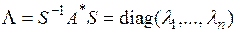, 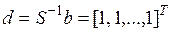. Матрица 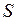находится с помощью матрицы управляемости: 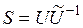, где 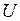матрица управляемости, а матрица 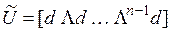невырожденная по построению.

Покажем, что если вектор 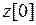принадлежит области

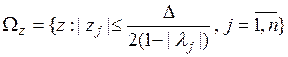, (14)

то 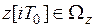при любом 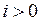. Действительно, уравнению (13) соответствуют уравнения

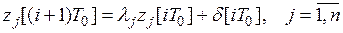, (15)

из которых при 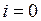с учетом 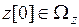следуют неравенства

,

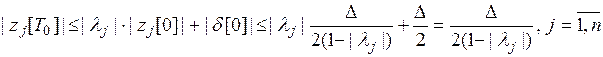т.е. выполняется условие 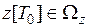. Аналогично показывается, что 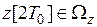и т.д., что и требовалось доказать.

При произвольных начальных условиях 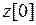для уравнений (15) справедливы решения

, ,

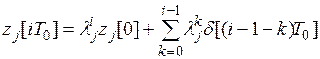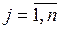для которых выполняются неравенства:

, .

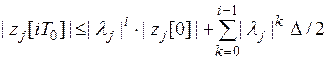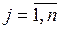Отсюда следует, что при 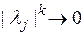, , 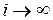с учетом равенства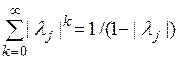

выполняется условие 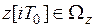. С помощью обратного преобразования 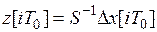и обозначения 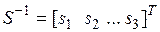получим область

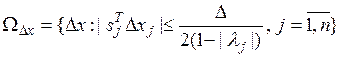. (16)

Таким образом, область (16) является оценкой сверху области изменения вектора 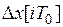в установившемся режиме, которая характеризует точность ЦАС и является более точной по сравнению с аналогичной оценкой, полученной с использованием функций Ляпунова. Отметим, что оценка (16) справедлива как при устойчивой, так и при неустойчивой разомкнутой системе (8). При этом даже в случае устойчивости разомкнутой системы в замкнутой системе (11) могут присутствуют автоколебания относительно установившегося режима 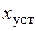. Если разомкнутая система неустойчива, то в замкнутой системе возникают незатухающие колебания, имеющие "квазислучайный" характер. Это связано с тем, что характеристика квантования по уровню 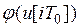в ЦАС имеет зону нечувствительности, и когда процесс 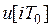попадает в нее, система размыкается, и в силу неустойчивости разомкнутой системы процесс 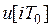стремится выйти из зоны нечувствительности.

В случае устойчивой разомкнутой системы или находящейся на границе устойчивости, оценка (16) для системы (8) может быть завышенной, т.к. в замкнутой системе могут отсутствовать автоколебания. При этом процесс 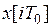стремится к положению равновесия 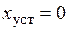, если разомкнутая система устойчива, или к отрезку покоя, соответствующему зоне нечувствительности характеристики 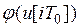, если находится на границе устойчивости.

Вопросы для самопроверки

1. В каких случаях в замкнутых ЦАС возникают незатухающие колебания?

2. За счет чего можно повысить точность ЦАС в установившемся режиме?