Однородные дифференциальные уравнения 1-го порядка

Определение 1. Уравнение 1-го порядка 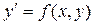называется однородным, если для его правой части при любых 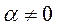справедливо соотношение 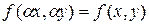, называемое условием однородности функции двух переменных нулевого измерения.

Пример 1. Показать, что функция 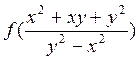- однородная нулевого измерения.

Решение.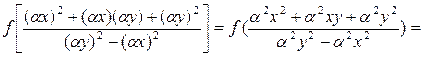

,

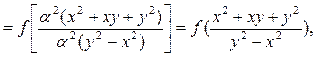
что и требовалось доказать.

Теорема. Любая функция 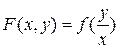- однородна и, наоборот, любая однородная функция 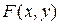нулевого измерения приводится к виду .

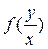Доказательство.

Первое утверждение теоремы очевидно, т.к. 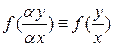. Докажем второе утверждение. Положим 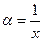, тогда для однородной функции 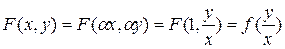, что и требовалось доказать.

Определение 2. Уравнение 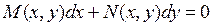(4.1)

в котором M и N – однородные функции одной и той же степени, т.е. обладают свойством 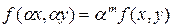при всех 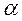, называется однородным.

Очевидно, что это уравнение всегда может быть приведено к виду 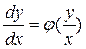(4.2) , хотя для его решения можно этого и не делать.

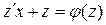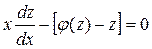Однородное уравнение приводится к уравнению с разделяющимися переменными с помощью замены искомой функции y по формуле y=zx, где z(x) – новая искомая функция. Выполнив эту подстановку в уравнении (4.2), получим: или или .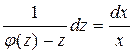

Интегрируя, получаем общий интеграл уравнения относительно функции z(x) 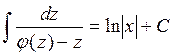, который после повторной замены 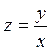дает общий интеграл исходного уравнения. Кроме того, если 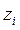- корни уравнения 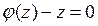, то функции 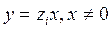- решения однородного заданного уравнения. Если же 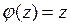, то уравнение (4.2) принимает вид

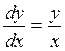и становится уравнением с разделяющимися переменными. Его решениями являются полупрямые: .

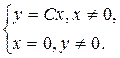Замечание. Иногда целесообразно вместо указанной выше подстановки использовать подстановку x=zy.

Дифференциальные уравнения, приводящиеся к однородным.

Рассмотрим уравнение вида 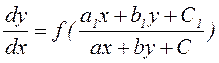. (5.1)

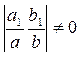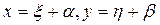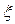Если , то это уравнение с помощью подстановки , где и 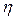- новые переменные, а 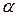и 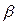- некоторые постоянные числа, определяемые из системы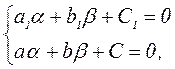

Приводится к однородному уравнению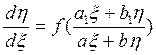

Если 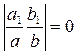, то уравнение (5.1) принимает вид

.

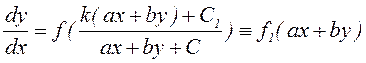Полагая z=ax+by, приходим к уравнению, не содержащему независимой переменной.

Рассмотрим примеры.

Пример 1.

Проинтегрировать уравнение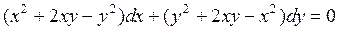

и выделить интегральную кривую, проходящую через точки: а) (2;2); б) (1;-1).

Решение.

Положим y=zx. Тогда dy=xdz+zdx и

.

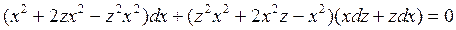Сократим на 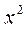и соберем члены при dx и dz:

.

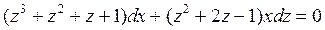Разделим переменные: .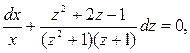

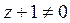Интегрируя, получим ;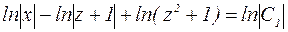

или , .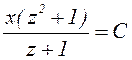

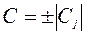Заменив здесь z на 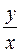, получим общий интеграл заданного уравнения в виде (5.2) 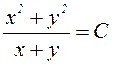или .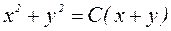

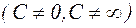Это семейство окружностей 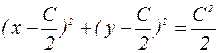, центры которых лежат на прямой y = x и которые в начале координат касаются прямой y + x = 0. Эта прямая y = -x в свою очередь частное решение уравнения.

Теперь режим задачи Коши:

А) полагая в общем интеграле x=2, y=2, находим С=2, поэтому искомым решением будет .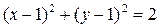

Б) ни одна из окружностей (5.2) не проходит через точку (1;-1). Зато полупрямая y = -x, проходит через точку и дает искомое решение.

Пример 2. Решить уравнение: .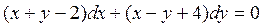

Решение.

Уравнение является частным случаем уравнения (5.1).

Определитель 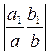в данном примере 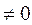, поэтому надо решить следующую систему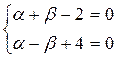

Решая, получим, что 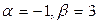. Выполняя в заданном уравнении подстановку 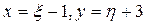, получаем однородное уравнение 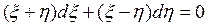. Интегрируя его при помощи подстановки 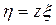, находим .

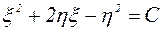Возвращаясь к старым переменным x и y по формулам 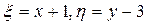, имеем .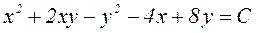