Скорость движения (истечения через отверстия и

Основные расчетные формулы

(кг/м³) – плотность

(н/м³) – удельный вес

ГИДРОСТАТИКА

р - давление или сжимающие напряжение (н/м² = Па)

Свойства:

Давление всегда направлено к поверхности по внутренней нормали.

Действует одинаково по всем направлениям (не зависит от угла наклона площадки)

Основное уравнение гидростатики:

р_А = р_о + р_в; р_в = h·γ

р_А – абсолютное давление;

р_о – давление действующее на поверхность жидкости;

р_в – весовое давление, т.е. давление столба жидкости.

р_в = h·γ

h – глубина расположения точки;

γ – удельный вес жидкости.

При атмосферном давлении на поверхности:

р_А = р_а + р_изб; р_изб = h_изб·γ

р_а – атмосферное давление;

р_изб – избыточное давление.

Выводы:

1) Закон Паскаля. Давление действующее на поверхность жидкости передается во все ее точки без изменения.

2) Любая горизонтальная плоскость проведенная в жидкости, является плоскостью равного давления.

3) Можем измерять величину давления эквивалентной ему высотой столба жидкости.

р = h·γ, отсюда h = р/γ

Например давление величиной в 1 атм. р = 1 кгс/см² соответствует

h = 10 м вод. столба

Сила давления жидкости на плоскую поверхность

Р = р_сS = h_сγS (н)

р_с = h_сγ – давление в центре тяжести при атмосферном давлении на поверхности

р_с = h_сγ + р_М, либо р_с = h_сγ – р_ВАК

h_с – глубина расположения центра тяжести поверхности (м);

S – площадь поверхности (м²).

Потенциальная энергия покоящейся жидкости величина постоянная, т.е. одинаковая для всех точек жидкости

Удельная энергия (напор)

Э = Е/G = Е/mg (м)

Z + h_п = Н_ГС = Э = const

Z – геометрический напор;

h_п – пьезометрический напор;

Н_ГС –гидростатический напор или полная удельная потенциальная энергия жидкости.

ГИДРОДИНАМИКА

Уравнение неразрывности

Q = V₁ω₁ = V₂ω₂ = const

Q – расход жидкости (м³/с);

V – средняя скорость потока (м/с);

Ω – площадь живого сечения потока (м²).

V_i = Q / ω_i – средняя скорость потока

Уравнение Бернулли для идеальной жидкости (при действии сил давления и сил тяжести)

где z - геометрический напор, м;

P/γ - приведенная пьезометрическая высота (если Р - абсолютное давление) или пьезометрическая высота (если Р - избыточное давление), м;

V²/2g - скоростной напор, м.

- гидростатический напор,

удельная потенциальная энергия жидкости

Н_ГС = Э – гидродинамический напор или полная удельная энергия

Уравнение Бернулли для реальной жидкости (с учетом сил трения (вязкости)).

Σh = h_пот = h_ℓ + h_м – потери энергии при движении жидкости от 1 до 2 сечений (м);

α= Е_КД /Е_КУ – коэффициент кинетический энергии (коэффициент Кориолиса);

h_ℓ - потери по длине.

(м)

λ – коэффициент гидравлического трения f(R_е·Δ);

h_м – потери на местных сопротивлениях.

(м)

РЕЖИМЫ ДВИЖЕНИЯ

Число (критерий) Рейнольдса

Для кругло-цилиндрических труб

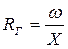(м)

R_Г – гидравлический радиус;

ω – площадь живого сечения потока (м²);

Х – смоченный периметр.

Ламинарный режим: Rе < Rе_кр ≈ 2320

Эпюра скорости при ламинарном движении.

u_max = 2V; α = 2; λ = f(Rе); λ = 64/Rе; h_ℓ = f (V^1…1,4)

Турбулентный режим: Rе > Rе_кр

Профиль скорости при турбулентном движении

Толщина ламинарной пленки δ уменьшается с увеличением скорости V (числа Рейнольдса)

u ≈ V; α = 1…1,4

В турбулентном режиме имеется три вида трения:

Гидравлически гладкие русла

λ = f(Rе) λ = 0,3164/Rе^0,25

Смешанное трение

λ = f(Rе;Δ)

Шероховатое трение, квадратичная область турбулентного режима

λ = f (Δ); λ = 0,11(Δ /d)^0,25

h_ℓ = f (V^1,7…2)

СКОРОСТЬ ДВИЖЕНИЯ (ИСТЕЧЕНИЯ ЧЕРЕЗ ОТВЕРСТИЯ И

НАСАДКИ)

(м/с)

-коэффициент скорости

Н_о – действующий (расчетный напор (м)

Расход жидкости

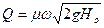(м³/с)

μ = φε – коэффициент расхода;

ω – площадь проходного (живого) сечения потока (м²);

Н_о – действующий напор (м).

Коэффициенты скорости φ расхода μ для отверстия и насадков

Вид	φ	μ
Отверстия в тонкой стенке при совершенном сжатии. При определении скорости в сжатом сечении струи	0,62	0,62
0,97	0,62
Внешний цилиндрический насадок (насадок Вентури) ≈ 0,75	0,82	0,82
Внутренний цилиндрический насадок	0,71	0,71
Сходящийся конический насадок (конфузор). Оптимальный угол конусности 12о…14о	0,96	0,94
Конический расходящийся насадок (диффузор). Оптимальный угол конусности 6о…7о	0,47	0,47
Коноидальный насадок	0,98	0,98

При расчете коротких трубопроводов

Расчет длинных трубопроводов

При расчете длинных трубопроводов основную долю в потерях составляют потери по длине. Диаметр труб выбирают по экономической скорости (≈ 1 м/с).

Н = h_пот.

Расчет ведется по формулам с использованием модуля расхода К (л/с; м³/с) который выбирают в зависимости от диаметра и шероховатости стенок трубы.

Время полного истечения жидкости из резервуара

(с)

W – начальный объем жидкости в резервуаре;

Q – расход при начальном напоре.

Время истечения от уровня Н₁ до Н₂

(с)

При проектировании и расчетах различных устройств в гидравлике используют теорию подобия и различные методики моделирования процессов.

Различают моделирование математическое и физическое.

Математическое моделирование основано на том, что одна и та же система уравнений может выражать различные физические явления в зависимости от того, какой смысл придается символам, входящим в уравнения.

Физическое моделирование – это воспроизведение изучаемого процесса или явления (оригинала) с сохранением его физической природы. Экспериментальные исследования на моделях проводятся, когда рассматриваемые явления не изучены и нет возможности описать их математически при помощи уравнений, формул, зависимостей и т.д.

Из теории подобия вытекают следующие правила моделирования:

1. Модель должна быть геометрически подобна оригиналу (натуральному образцу).
2. Процессы, протекающие в модели и в оригинале, должны принадлежать к одному классу явлений, то есть они описываются одинаковыми дифференциальными уравнениями.
3. Начальные и граничные условия в модели, выраженные в безразмерной форме, в числовом виде должны быть тождественны безразмерным условиям оригинала.
4. Одноименные безразмерные критерии должны быть численно равны в модели и в оригинале (натуральном образце).

Геометрически подобными являются фигуры, все линейные размеры которых пропорциональны между собой, а углы – равны. Такой коэффициент пропорциональности называют линейным масштабом подобия М_ℓ.

где ℓ_н – размер натурального образца;

ℓ_м – соответствующий размер модели.

М_ℓ - масштабный коэффициент или масштаб подобия

Кинематически подобными называются такие геометрически подобные системы, в которых направления скоростей и ускорений во всех сходственных эпюрах одинаковы, а величины скоростей и ускорений в соответствии – пропорциональны. Коэффициент пропорциональности скоростей в этом случае называют масштабом скорости, а коэффициент пропорциональности ускорений – масштаб ускорений KW (М_v).

;

Динамически подобными называются такие системы, в которых, кроме геометрического подобия, выполняются условия:

1. в сходственных точках действуют одноименные силы (одной и той же природы);
2. для любой пары сходственных точек соотношения сил одинаковое;
3. силы, действующие на любую пару сходственных точек, одинаково ориентированы относительно друг друга и относительно границ системы.

Используется так же временное подобие, при котором время протекания процессов в сходных точках модели и натурального образца подчиняются зависимости:

Для проверки адекватности модели натуральному образцу используются различные безразмерные критерии подобия. Чаще других в гидравлике используются:

Критерий Фруда: =

Критерий показывает отношений сил инерции в системе к силам тяжести, т.е. применяется при преобладающем влиянии сил тяжести.

Критерий Эйлера:

Показывает отношении сил давления к силам инерции, применяется при преобладающем влиянии сил давления.

Критерий (число) Рейнольдса:

Показывает отношение сил инерции к силам трения, применяется при преобладающем влиянии сил трения (вязкости).

Критерий гомохромности:

Показывает отношение локальных сил инерции к конвективным силам инерции, применяется при преобладающем значении времени протекания процессов.

Причем, для модели и натурального образца должно выполнятся условие равенства одного или нескольких критериев в сходных точках.

и т.д.