Понятие графа. Способы задания графа. Методика выделения компонента связности в графе

Графические представления – удобный способ иллюстрации содержания различных понятий, относящихся к другим способам формализованных представлений (см. диаграммы Эйлера).

Все более распространенными становятся представления количественных характеристик, взаимосвязей между объектами в виде разного рода одно-, двух- и более мерных гистограмм, круговых диаграмм, других аналогичных способов представления в виде тех или иных геометрических фигур, по наглядным характеристикам которых (высоте, ширине, площади, радиусу и пр.) можно судить о количественных соотношениях сравниваемых объектов, значительно упрощая их анализ.

Мощным и наиболее исследованным классом объектов, относящихся к графическим представлениям, являются так называемые графы, изучаемые в теории графов. Теория графов имеет огромные приложения, так как ее язык, с одной стороны, нагляден и понятен, а с другой – удобен в формальном исследовании. На языке теории графов формулируются и решаются многие задачи управления, анализа и проектирования организационных структур управления, анализа процессов функционирования и целеполагания, многие задачи принятия решений в условиях неопределенности и др.

Следует иметь в виду, что при изображении графа не все детали рисунка одинаково важны; в частности, несущественны геометрические свойства ребер (длина, кривизна и т.д.) и взаимное расположение вершин на плоскости.

Графические представления в узком смысле – это описание исследуемой системы, процесса, явления средствами теории графов в виде совокупности двух классов объектов: вершин и соединяющих их линий – ребер или дуг. Графы и их составляющие характеризуются определенными свойствами и набором допустимых преобразований (операций) над ними.

Графом G(V,E) называется совокупность двух множеств - непустого множества V (множества вершин) и множества Е неупорядоченных пар различных элементов множества V (Е - множество ребер).

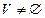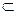G(V,E): , E VxV.

Число вершин графа G обозначим р, а число ребер – q.

р(G) = |V| q(G) = |E|.

Часто рассматриваются следующие родственные графам объекты.

1. Если элементами множества Е являются упорядоченные пары, то граф называется ориентированным (или орграфом). В этом случае элементы множества V называются узлами, а элементы множества 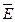- дугами (G(V, )).

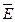2. Если элементом множества Е может быть пара одинаковых (не различных) элементов V, то такой элемент множества Е называется петлей, а граф называется графом с петлями (или псевдографом).

3. Если Е является не множеством, а набором, содержащим несколько одинаковых элементов, то эти элементы называются кратными ребрами, а граф называется мультиграфом.

Далее выражение: граф G(V,E) означает неориентированный граф без петель и кратных ребер.

Обычно граф изображают диаграммой: вершины - точками (или кружками), ребра - линиями.

Примеры.

1. . .

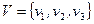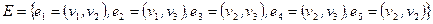Т.о. это неориентированный граф с петлей и кратными ребрами.

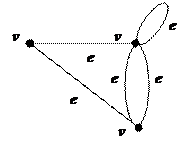2. . .

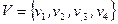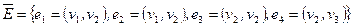Рис. 1. Неориентированный граф с петлей и кратными ребрами.

Т.о. это ориентированный граф с петлей и кратными ребрами.

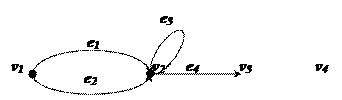Рис. 2. Ориентированный граф с петлей и кратными ребрами.

3. 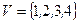. 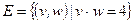, т.о.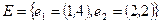

Рис. 3. Неориентированный граф с петлей.