Компоненты связности графа

Лабораторная работа №4. ТЕОРИЯ ГРАФОВ.

РАСКРАСКА НЕОРИЕНТИРОВАННЫХ ГРАФОВ

Цель работы: изучить особенности неориентированных графов и основные определения; научиться находить хроматическое число и хроматический класс для графа.

Неориентированные графы

Основные понятия

Понятие неориентированного графа считают более общим по отношению к понятию ориентированного графа .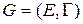

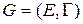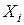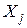Ребром графа называется такая пара элементов и , для которой

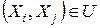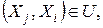или (4.1)

т.е. пара вершин, связанных дугами в обоих направлениях либо одной дугой в каком-либо направлении.

Ребро обозначается так:

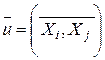или 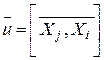. (4.2)

Обозначим множество ребер графа через .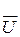

Множество вершин 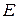вместе с множеством ребер 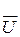определяют неориентированный граф, который обозначается через

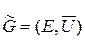. (4.3)

Каждому ориентированному графу 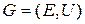можно однозначно поставить в соответствие неориентированный граф 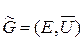. Обратное, очевидно, неверно.

Если в ориентированных графах (рис. 4.1, 4.2) дуги заменить

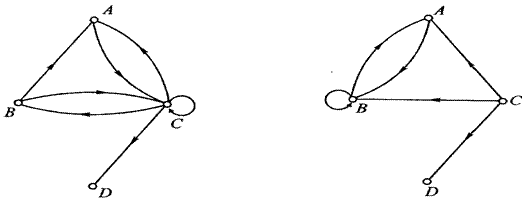Рис. 4.1 Рис. 4.2

ребрами, то получится неориентированный граф (рис. 4.3).

В некоторых случаях неориентированный граф можно воспринимать как симметрический граф без петель. Например, граф 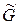(рис. 4.3) и граф 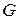(рис. 4.4) не различаются.

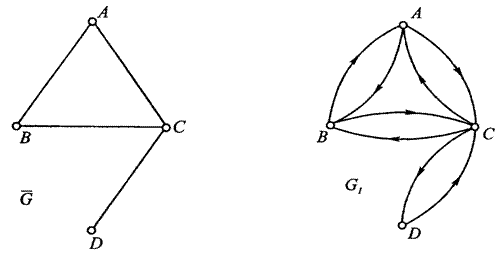Рис. 4.3 Рис. 4.4

Однако понятие неориентированности не всегда совпадает с понятием двусторонней ориентированности.

Например, в транспортной сети симметрия некоторых дуг может сочетаться с антисимметрией их пропускных способностей.

Неориентированному графу 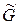соответствует 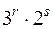различных графов 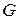, где 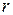- число ребер, 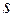- число вершин. Например, граф, изображенный на рис. 4.5, имеет 14 дуг и 8 ребер.

Цепь – такая последовательность ребер 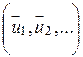, в которой каждое ребро 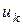соприкасается одним из концов с ребром 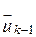, а другим – с 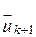(если они существуют). Далее мы намеренно используем ориентированные графы при иллюстрации компонентов неориентированных графов с целью уяснения их родства и различия. При этом следует мысленно заменить дуги соответствующими ребрами.

Например, для графа, изображенного на рис. 4.1, цепи обозначаются так:

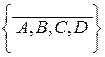и .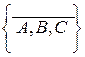

Длиной цепи называется число ребер, которые она содержит.

Простая и элементарная цепи определяются аналогично пути, только вместо дуг рассматриваются ребра.

Цикл – это конечная цепь, которая начинается и заканчивается в одной и той же вершине. Например, для графа, изображенного на рис. 4.5, цепи 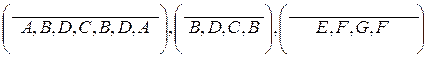яв-ляются циклами.

Эквивалентными считаются циклы, проходящие через одни и те же вершины в одинаковом порядке. Например, для графа, показанного на рис. 4.5,

.

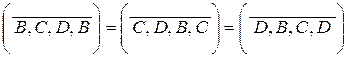Понятия простого цикла и элементарного цикла определяются аналогично соответствующим понятиям для контуров, только вместо дуг рассматриваются ребра.

Связный граф .

Граф 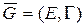называется связным, если для всех 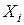и 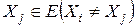всегда существует цепь из вершины 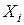в вершину .

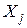Сильно связный граф всегда связный.

Например, граф 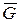(см. рис. 4.3) связный, но не сильно связный; а граф 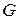(см. рис. 4.5) – не связный и ему соответствующий граф 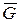также не связный.

Компоненты связности графа.

Совокупность вершин графа ( 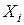), которые можно соединить цепью, обозначим через .

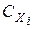Компонентой связности 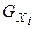называется подграф графа 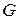, порожденный .

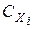Например, граф 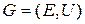и ему соответствующий неориенти-рованный граф 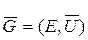(см. рис. 2.62) имеют две компоненты связности: .

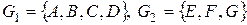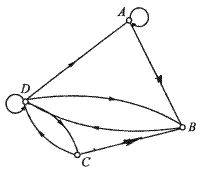
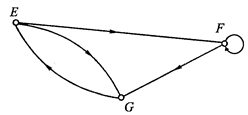
Рис. 4.5

Пусть 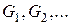- компоненты связности, порожденные подмно-жествами вершин .

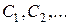Тогда имеют место следующие соотношения:

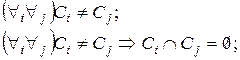(4.4)

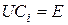, а также .

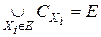Далее под словом «граф» подразумеваем неориентированный граф, ассоциируя по-прежнему дуги как ребра.

Степенью вершины 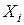называется число ребер, для которых одним из концов служит 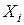(другой конец отличен от 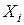). Степень вершины 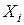обозначается через .

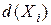Например, для графа, изображенного на рис. 4.5,

.
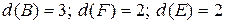