Параметрическая (числовая) информация. Дискретизация непрерывных сообщений
Для представления количественной информации чаще всего используются числа. По сравнению с представлением величин непрерывными зависимостями они дают значительные преимущества в возможностях обработки и хранения информации. Именно поэтому непрерывные сообщения часто “оцифровывают”, то есть представляют как последовательность чисел.
Числовая информация, как и символьная, по своей природе дискретна, так как она может быть представлена ограниченным набором символов (в частности, цифр).
На Рис.1.3 показана дискретизация непрерывной зависимости U(t). Она включает две составляющих:
- дискретизацию по времени с шагом  t;
t;
- дискретизацию (квантование) по уровню с шагом  U.
U.
Благодаря этим двум этапам всю зависимость U(t) можно представить как последовательность дискретных значений, которым соответствуют числа.
Очевидно, что точность дискретизации по уровню может быть выбрана как угодно большой
Важно, что непрерывную информацию с помощью оцифровки (дискретизации) принципиально в любом случае можно представить, как дискретную с любой необходимой точностью. В тоже время, обратное преобразование иногда невозможно (например, для символов). Таким образом, дискретная форма представления информации является наиболее общей.
| Δ |
| t |
| U(t) |
Рис. 1.3 Представление аналоговой информации в виде дискретных значений
В соответствие с формами представления информации выделяют и типы дискретных и непрерывных сообщений. Первые состоят из знаков, принадлежащих к определенному алфавиту. Вторые включают непрерывно меняющиеся во времени величины.
Принципиально важно, что непрерывная информация в любом случае может быть преобразована к дискретной, тогда как обратное преобразование возможно не всегда.
Действительно, непрерывную зависимость некоторых величин можно дискретизировать, если задавать их соответствие в ограниченном наборе точек. При этом точность такого преобразования принципиально может быть задана достаточно высокой, чтобы не потерять информацию. А вот однозначно восстановить неизвестную кривую по ограниченному набору точек возможно не всегда. Мы будем рассматривать дискретную форму представления информации, как основную.
Таким образом, информация может быть двух видов: дискретная информация и непрерывная (аналоговая). Дискретная информация характеризуется последовательными точными значениями некоторой величины, а непрерывная - непрерывным процессом изменения некоторой величины. Непрерывную информацию может, например, выдавать датчик атмосферного давления или датчик скорости автомашины. Дискретную информацию можно получить от любого цифрового индикатора: электронных часов, счетчика магнитофона и т.п.
Дискретная информация удобнее для обработки человеком, но непрерывная информация часто встречается в практической работе, поэтому необходимо уметь переводить непрерывную информацию в дискретную (дискретизация) и наоборот. Модем (это слово происходит от слов модуляция и демодуляция) представляет собой устройство для такого перевода: он переводит цифровые данные от компьютера в звук или электромагнитные колебания-копии звука и наоборот.
При переводе непрерывной информации в дискретную важна так называемая частота дискретизации 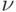 , определяющая период (
, определяющая период ( 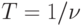 ) между измерениями значений непрерывной величины (рис. 1.4).
) между измерениями значений непрерывной величины (рис. 1.4).
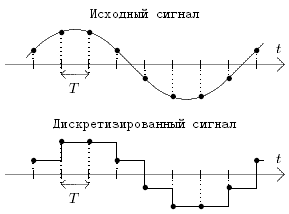
Рис. 1.4. Частота дискретизации.
Чем выше частота дискретизации, тем точнее происходит перевод непрерывной информации в дискретную. Но с ростом этой частоты растет и размер дискретных данных, получаемых при таком переводе, и, следовательно, сложность их обработки, передачи и хранения. Однако для повышения точности дискретизации необязательно безграничное увеличение ее частоты. Эту частоту разумно увеличивать только до предела, определяемого теоремой о выборках, называемой также теоремой Котельникова или законом Найквиста.
Любая непрерывная величина описывается множеством наложенных друг на друга волновых процессов, называемых гармониками, определяемых функциями вида  , где
, где 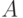 - это амплитуда,
- это амплитуда, 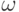 - частота,
- частота, 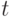 - время и
- время и 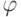 - фаза.
- фаза.
Теорема о выборках утверждает, что для точной дискретизации ее частота должна быть не менее чем в два раза выше наибольшей частоты гармоники, входящей в дискретизируемую величину
Примером использования этой теоремы являются лазерные компакт-диски, звуковая информация на которых хранится в цифровой форме. Чем выше будет частота дискретизации, тем точнее будут воспроизводиться звуки и тем меньше их можно будет записать на один диск, но ухо обычного человека способно различать звуки с частотой до 20КГц, поэтому точно записывать звуки с большей частотой бессмысленно. Согласно теореме о выборках частоту дискретизации нужно выбрать не меньшей 40КГц (в промышленном стандарте на компакт-диске используется частота 44.1КГц).
При преобразовании дискретной информации в непрерывную, определяющей является скорость этого преобразования: чем она выше, с тем более высокочастотными гармониками получится непрерывная величина. Но чем большие частоты встречаются в этой величине, тем сложнее с ней работать. Например, обычные телефонные линии предназначены для передачи звуков частотой до 3КГц. Связь скорости передачи и наибольшей допустимой частоты подробнее будет рассмотрена далее.
Устройства для преобразования непрерывной информации в дискретную обобщающе называются АЦП (аналого-цифровой преобразователь) или ADC (Analog to Digital Convertor, A/D), а устройства для преобразования дискретной информации в аналоговую - ЦАП (цифро-аналоговый преобразователь) или DAC (Digital to Analog Convertor, D/A).
