Теплопроводность однородной пластины
Симметричные условия охлаждения (граничные условия третьего рода)
Дано: тонкая пластина, толщиной 2d площадью поверхности F, м2 с коэффициентом теплопроводности l=const, с объемным тепловыделением qv находится в среде с температурой tж=const (рис. 3.1). Задан коэффициент теплоотдачи 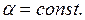 Условие "тонкой" пластины предполагает пренебрежимо малый отток тепла в среду с торцов, теплота передается в среду только с боковых поверхностей пластины.
Условие "тонкой" пластины предполагает пренебрежимо малый отток тепла в среду с торцов, теплота передается в среду только с боковых поверхностей пластины.
 Определить: уравнение температурного поля t=f(x), тепловой поток Q, отводимый с боковой поверхности пластины.
Определить: уравнение температурного поля t=f(x), тепловой поток Q, отводимый с боковой поверхности пластины.
Температурное поле пластины описывается дифференциальным уравнением теплопроводности (1.13). Для стационарного режима 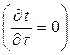 при отсутствии теплоотдачи с торцов
при отсутствии теплоотдачи с торцов 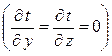 оно запишется в виде
оно запишется в виде
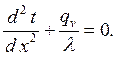 | (3.1) |
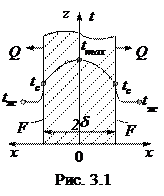
Дифференциальное уравнение второго порядка требует два дополнительных условия однозначности для определения констант интегрирования. Такими условиями являются граничное условие третьего рода (заданы tж, 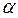 ), которое на основании (1.15) для данной задачи запишется в виде
), которое на основании (1.15) для данной задачи запишется в виде
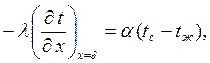 | (3.2) |
и условие максимума температуры в центре пластины
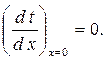 | (3.3) |
Система уравнений (3.1) – (3.3) является математической постановкой задачи.
Граничные условия на поверхностях пластины одинаковы, тепловые потоки, отводимые с поверхностей, одинаковы поэтому можно рассматривать лишь одну половину пластины, например правую, для которой записано граничное условие (3.2).
После интегрирования (3.1) получим
 | (3.4) |
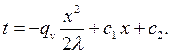 | (3.5) |
Уравнение (3.5) - общий интеграл уравнения (3.1). Постоянные интегрирования с1 и с2 определяются с помощью граничных условий (3.2) и (3.3). Из уравнения (3.4) с учетом (3.3) получим
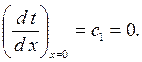
Из уравнения (3.4) при х=d имеем
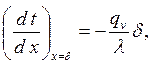
а из (3.5) при х=d
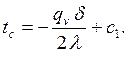
Значения 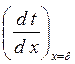 и tс подставим в (3.2) и найдем постоянную интегрирования
и tс подставим в (3.2) и найдем постоянную интегрирования
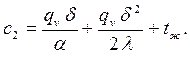
После подстановки значений с1 и с2 в (3.5) получим уравнение температурного поля t=f(x) при граничных условиях третьего рода
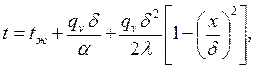 | (3.6) |
где х – текущая координата.
Уравнение (3.6) – симметричная парабола (рис. 3.1). Максимальная температура (tтах) – в центре пластины (х=0), минимальная (tс) – на поверхности пластины (х=d). При этих условиях из (3.6) можно получить расчетные формулы для максимальной температуры и температуры поверхности пластины:
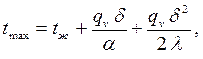 | (3.7) |
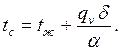 | (3.8) |
Если в уравнение (3.6) подставить значение tс согласно (3.8), то получим уравнение температурного поля пластины t=f(x) при граничных условиях первого рода
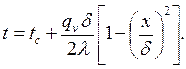 | (3.9) |
Тепловой поток, рассеиваемый поверхностью F, рассчитывается по формулам:
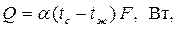 | (3.10) |
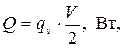 | (3.11) |
где V, м3 - объем пластины.
Суммарный тепловой поток, рассеиваемый двумя боковыми поверхностями, вдвое больше, т.к. площадь поверхности охлаждения Fохл=2F, тепловыделяющий объем - V, м3.
