Свойства преобразования Фурье
1. Прямое и обратное преобразование Фурье являются линейными операторами, следовательно, действует принцип суперпозиции. Если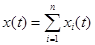 
, то 
.
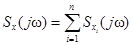2. Прямое и обратное преобразование Фурье являются взаимно однозначными.
3. Свойство запаздывания.
Если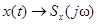 
, то
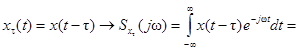
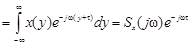
(в данном случае использованы подстановки: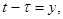 
).
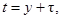
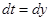4. Спектральная функция δ-функции.
Используя общее выражение спектральной функции и фильтрующее свойство δ-функции, получим
.
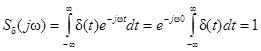5. Спектральная функция комплексного гармонического сигнала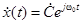 
.
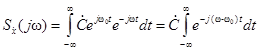(2.5)
Используя одно из определений δ-функции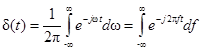 
и выполняя в нём взаимную замену t и w (или f), получим
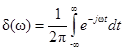и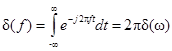 
.
Сопоставляя полученный результат с (2.5), имеем
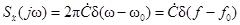(2.6)
6. Скалярное произведение комплексных сигналов в спектральной области. Пусть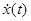 
и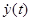 
– комплексные функции на интервале (–T/2, T/2). Их скалярное произведение
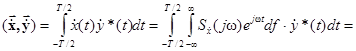
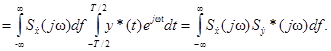
Из полученного результата для вещественных функций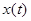 
вытекает равенство Парсеваля (обобщённая формула Рэлея)
,
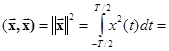
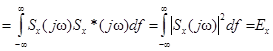где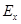 
– энергия сигнала ,
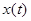а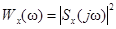 
– спектральная плотность энергии.
Для сигналов x(t), заданных на бесконечной оси времени (–¥,+¥), с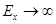 
, но имеющих ограниченную мощность 
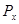, вместо спектральной плотности энергии 
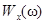можно использовать спектральную плотность мощности (энергетический спектр)
.
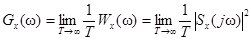Тогда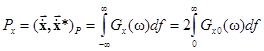 
, т.к.
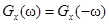и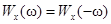 
– чётные функции, 
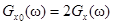– односторонняя спектральная плотность мощности (энергетический спектр).
7. Скалярное произведение комплексных сигналов 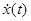и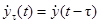 
в спектральной области.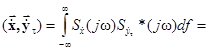 
.
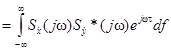Пр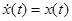и 
и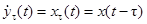 
, 
–
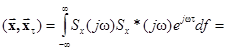
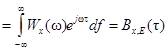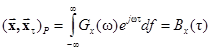– корреляционная функция сигнала x(t).
Из последнего выражения вытекают важные соотношения между корреляционной функцией и энергетическим спектром сигнала
,
.
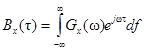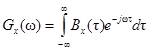8. Спектр произведения сигналов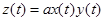 
.
, 
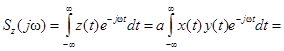
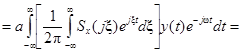
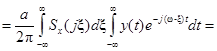
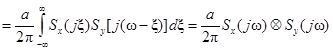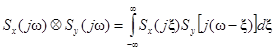– – свертка функци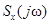й 
и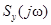 
.
Таким образом, спектральная функция произведения двух сигналов является свёрткой их спектральных функций.
Справедливо также и обратное соотношение
.
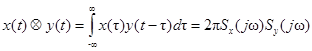9. Свойство смещения спектра.
Если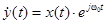 
, то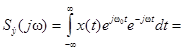 
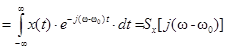. (2.7)
10. Ширина спектра.
Теоретически ширина спектра сигналов бесконечна. Однако, учитывая, что интенсивность спектральных составляющих реальных сигналов уменьшается с ростом их частоты (не обязательно монотонно), можно ввести понятие практической (конечной) ширины спектров (рис. 2.3 и 2.4). Практическую ширину спектра DW можно определять как ширину частотного интервала, в пределах которого амплитудный спектр S(w) не меньше некоторого условного уровня g (например g = 0,1) от S(w)max или энергия (мощность) сигнала составляет определённую часть g (например g = 0,9) от полной
.
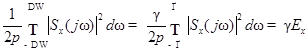Для импульсов простых форм (прямоугольной, треугольной и т.п.), спектральная функция которых периодически принимает нулевые значения с ростом частоты (рис. 2.3 и 2.4), практическую ширину спектра часто определяют по первому или второму или иному «нулю» амплитудного спектра.
Независимо от способа определения практической ширины спектра Т-финитного сигнала выполняется общая закономерность – произведение практической ширины спектра на длительность сигнала Dt есть константа C, зависящая только от формы импульса
DW·Dt = C.
Это соотношение имеет фундаментальное значение в теории связи. Из него вытекает, что чем короче сигнал, тем шире его спектр и, следовательно, тем более широкополосный канал требуется для его передачи.
Контрольные вопросы
1. Какие сигналы являются периодическими?
2. Какой математический аппарат используется для спектрального анализа периодических сигналов?
3. Что называют амплитудным и фазовым спектрами периодического сигнала?
4. Какими свойствами обладают спектры периодических сигналов?
5. Как вычисляют амплитуды и фазы спектральных составляющих периодических сигналов?
6. Какие сигналы называют Т-финитными?
7. Какой математический аппарат используется для спектрального анализа Т-финитных сигналов?
8. Что такое спектральная функция (спектральная плотность амплитуд) сигнала и какова её размерность?
9. Что понимают под амплитудным и фазовым спектрами Т-финитного сигнала?
10. Как изменяется спектр сигнала в результате его задержки на время t?
11. Что представляет собой спектр d-функции?
12. Какова спектральная функция гармонического колебания?
13. Как можно вычислить скалярное произведение сигналов в спектральной области?
14. Что представляют собой спектральные плотности энергии и мощности сигналов? Каковы их размерности и свойства?
15. Что представляет собой корреляционная функция сигнала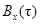 
?
16. Как вычисляют спектр произведения сигналов?
17. Как изменяется спектр сигнала в результате его умножения на гармоническое колебание?