Основная теорема о лебеговом продолжении меры.
Совокупность M всех измеримых по Лебегу множеств A 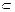 E является
E является 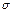 - алгеброй с единицей Е , а внешняя мера
- алгеброй с единицей Е , а внешняя мера 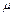 *(A) является
*(A) является 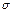 - аддитивным продолжением
- аддитивным продолжением
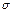 - аддитивная меры m с полукольца S на
- аддитивная меры m с полукольца S на 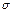 - алгебру M .
- алгебру M .
Доказательство.
Покажем, что M содержит S и * совпадает с на S .
Действительно, для всякого множества A 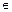 S справедливо:
S справедливо: 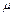 * (A
* (A 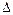 A) =
A) =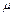 *(
*( 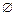 )= 0 ,
)= 0 ,
поэтому А измеримо. Далее, для всякого покрытия множества A 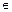 S конечной или счётной системой множеств Ai
S конечной или счётной системой множеств Ai 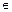 S справедливо:
S справедливо:
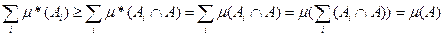 ,
,
и равенство достигается, например, при А1 = А , А2 = А3 = … = 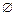 .
.
Покажем, что * монотонна на M .
Действительно, если A 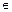 M , В
M , В 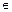 M , A
M , A 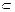 В , то
В , то 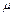 * (A)
* (A) 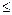
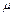 * (В) , так как всякое покрытие множества В конечным или счётным набором множеств из полукольца S будет одновременно и покрытием множества А .
* (В) , так как всякое покрытие множества В конечным или счётным набором множеств из полукольца S будет одновременно и покрытием множества А .
(3) Покажем, что 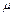 * полуаддитивна на M, то есть
* полуаддитивна на M, то есть
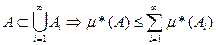
Действительно, так как
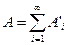 , где
, где 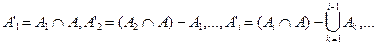 ,
,
и при этом A’i 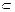 Ai , A’i
Ai , A’i 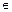 S и A’I
S и A’I 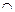 A’j =
A’j = 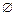 при i
при i 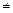 j , то
j , то
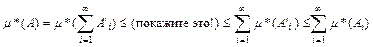
Покажем, что M - алгебра с единицей Е .
Нам нужно показать, что объединение, пересечение и разность любых двух измеримых множеств А1 и А2 измеримо. Действительно, пусть А1 и А2 произвольные измеримые множества. Это означает, что
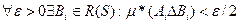
А так как
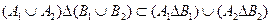
(проверьте это самостоятельно!), то
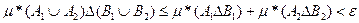
Но (В1 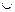 В2)
В2) 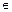 R(S) , поэтому множество А1
R(S) , поэтому множество А1 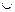 А2 измеримо.
А2 измеримо.
Измеримость дополнения всякого измеримого множества следует из равенства
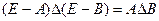
Измеримость пересечения двух измеримых множеств следует из равенства
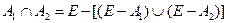
(5) Проверим, что для любых двух множеств А и В из Е выполняется:
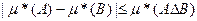
Действительно, так как А 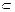 В
В 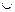 (А
(А 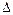 В) и В
В) и В 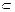 А
А 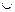 (А
(А 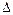 В) , то, в силу (3), имеем
В) , то, в силу (3), имеем
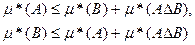
Поэтому
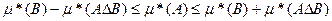
(6) Покажем, что 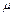 * аддитивна на M, то есть
* аддитивна на M, то есть
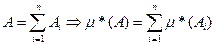
С учётом индукции достаточно проверить справедливость этого утверждения при n = 2 . Пусть множества А1 и А2 измеримы и А1 + А2 = А . Покажем, что
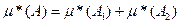
Так как множества А1 и А2 измеримы, то найдутся множества В1 и В2 из кольца R(S) такие, что
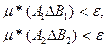

Так как множества А1 и А2 не пересекаются, то
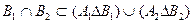
(проверьте это самостоятельно!), и, следовательно,
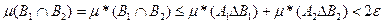
Далее, используя (5) , получим
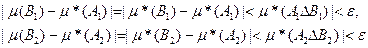
Так как мера 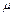 аддитивна на R(S) , то
аддитивна на R(S) , то
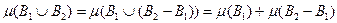
Добавив к обеим частям этого равенства m (В1 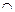 В2) , получим
В2) , получим
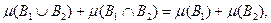
откуда
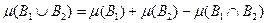
Воспользовавшись выше доказанными неравенствами, получим:
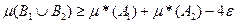
Заметим теперь, что
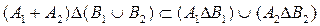
(проверьте это самостоятельно!). Поэтому
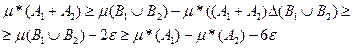
В силу возможности выбрать число 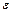 > 0 произвольно малым заключаем, что
> 0 произвольно малым заключаем, что
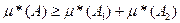
С другой стороны, так как объединение любых не более чем счётных покрытий множеств А1 и А2 является не более чем счётным покрытием множества А = А1 + А2 , то
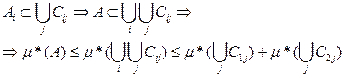
Поэтому
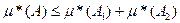
Итого получаем:
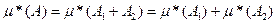
(7) Покажем, что 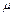 *
* 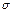 -аддитивна на M, то есть
-аддитивна на M, то есть
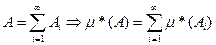
Действительно, для любом натурального n справедливо:
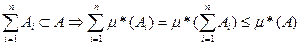
Переходя в этом неравенстве к пределу при n 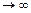 , получаем:
, получаем:
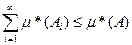
Доказательство противоположного неравенства проводится в полной аналогии с окончанием доказательства пункта (6) (проведите его самостоятельно!) .
