Построение доверительных интервалов

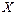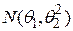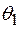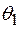1a) Если наблюдаемая случайная величина имеет нормальный закон распределения с неизвестным математическим ожиданием и неизвестной дисперсией , то доверительный интервал для математического ожидания имеет вид:

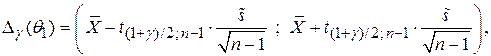
где 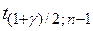– 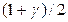- квантиль распределения Стьюдента 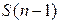с
(n—1) степенью свободы, 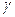– доверительная вероятность, 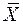- выборочное среднее 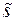- выборочная дисперсия.

При больших 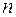(практически при 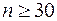) распределение Стьюдента приближается (в смысле слабой сходимости) к стандартному нормальному закону распределения, поэтому в этом случа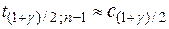е , где 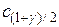– 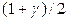-квантиль нормального распределения. Доверительный интервал для математического ожидания в этом случае будет строиться по закону:

,

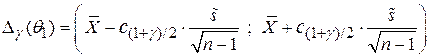Квантиль распределения нормального распределения определяется формулой:

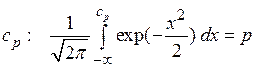
Будем искать 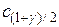при помощи функции cdfnor.

После подстановки значений получим: ∆_γ(θ₁)= ( -0.157761;0.325398)

1б) Доверительный интервал для дисперсии 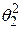наблюдаемой случайной величины 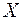, распределенной по нормальному закону 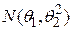, при неизвестном математическом ожидании 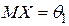имеет вид:

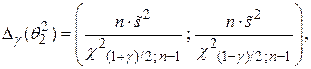
где 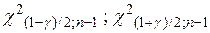– соответствующие квантили распределения .

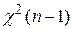Хи-квадрат 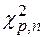квантиль распределения определяем по формуле:

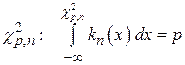, где .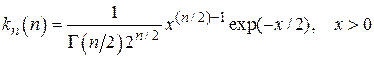

При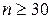

,

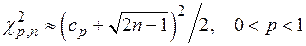где 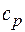— квантиль нормального распределения.

С использованием центральной предельной теоремы можно показать, что приближенным (асимптотическим) доверительным интервалом для дисперсии 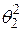нормально распределенной 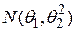случайной величины 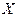с неизвестным математическим ожиданием 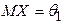является интервал:

,

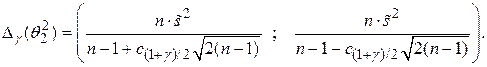После подстановки значений получим: ∆_γ(θ₂²)= (8.751177; 13.438808)

2) Если наблюдаемая случайная величина 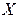имеет нормальный закон распределения 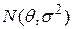с неизвестным математическим ожиданием 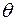и известной дисперсией 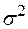, то доверительный интервал для математического ожидания 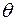имеет вид:

,

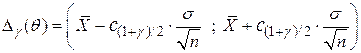∆_γ(θ)= (-0.343151; 0.646209)

3) Доверительный интервал для дисперсии 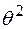наблюдаемой случайной величины 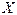, распределенной по нормальному закону 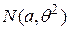, при известном математическом ожидании 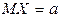имеет вид:

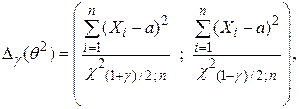
∆_γ(θ²)= (9.852264 ; 12.325678)

Заметим, что настоящие характеристики попадают в найденные для них доверительные интервалы.

Критерий Пирсона

Пусть имеем выборку объёма n 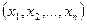, полученную при n наблюдениях над случайной величиной X, закон распределения которой неизвестен. Требуется проверить гипотезу о том, что величина X имеет нормальный закон распределения, пользуясь критерием χ² Пирсона. Рассмотрим отдельно случаи неизвестных и известных параметров распределения.

Используем полученные в 2.1.1 интервалы группировки, объединяем некоторые из них так, чтобы в каждом из интервалов частота группировки была не менее 5.

Составим таблицу для получившихся интервалов группировки:

Номер интервала	Интервал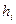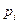
	[-9.599971; -7.8510942)		0.0063158	0.0036113	0.0028270
	[-7.8510942; -6.1022174)		0.0231579	0.0132416	0.0106259
	[-6.1022174; -4.3533406)		0.0589474	0.0337058	0.0300104
	[-4.3533406; - 2.6044638)		0.1305263	0.0746344	0.0636846
	[- 2.6044638;- 0.8555870)		0.1642105	0.0938949	0.1015442
	[- 0.8555870; 0.8932898)		0.2021053	0.1155629	0.1216561
	[0.8932898; 2.6421666)		0.1852632	0.1059327	0.1095143
	[2.6421666; 4.3910434)		0.1347368	0.0770419	0.0740739
	[4.3910434; 6.1399202 ]		0.0568421	0.0325021	0.0376459
	[6.1399202; 7.8887969 ]		0.0378947	0.0216680	0.0143757
Σ

Здесь 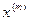– границы интервалов группировки;

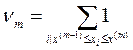– частоты значений;

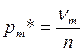– относительные частоты;

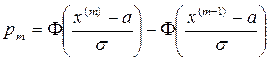– теоретические значения вероятности попадания в интервал;

Φ(x) – функция Лапласа;

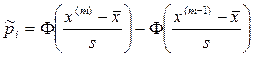– выборочные значения вероятности попадания в интервал.

Найдём значения статистик для случаев известных и неизвестных параметров распределения:

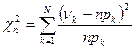– статистика для случая известных параметров. Здесь N – количество интервалов группировки.

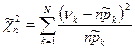– статистика для случая неизвестных параметров.

Полученные значения статистик:

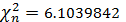
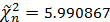
Определим пороги для обоих случаев:

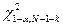– порог. Здесь k – число неизвестных параметров распределения.

Таким образом,

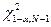– порог для случая известных параметров распределения,

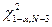– порог для случая неизвестных параметров распределения.

Получаем следующие пороги:

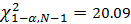
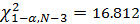
Сравним значения соответствующих статистик и порогов.

Значения статистик намного меньше, чем получившиеся пороги, следовательно, можно принять гипотезы о видах распределения, как с известными, так и с неизвестными параметрами.

Задание №2. Тут надо высчитать и записать

Имеем случайную величину X с плотностью вероятностей:

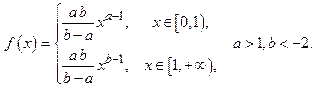
Рассчитаем аналитически числовые характеристики этой случайной величины.

Математическое ожидание X равно:

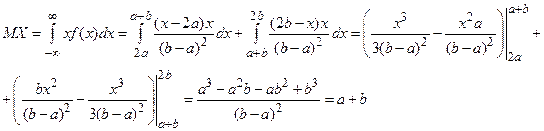
Подставим данные значения и получим, .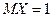

Найдем дисперсию.

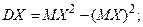
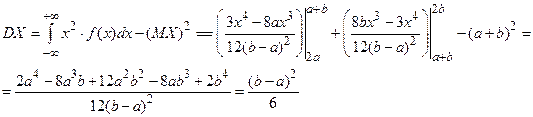
Подставляем данные значения, получаем 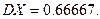17/81

Найдем функцию распределения:

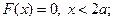
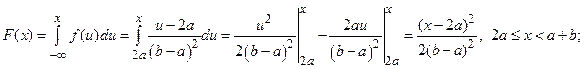
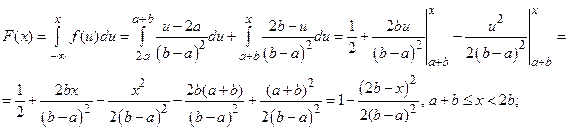
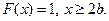
Подставляя значения, получим:

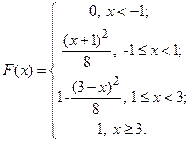
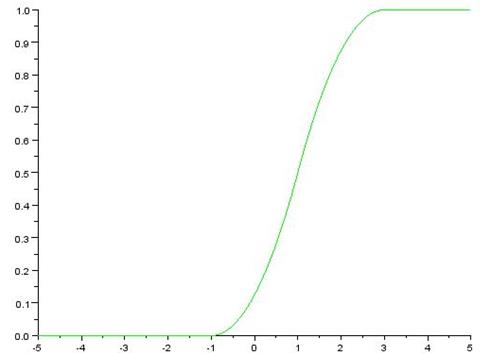
Построим графики функции распределения и плотности вероятности.

График плотности вероятностей:

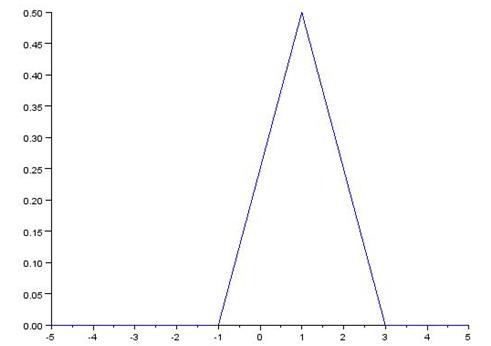
График функции распределения:

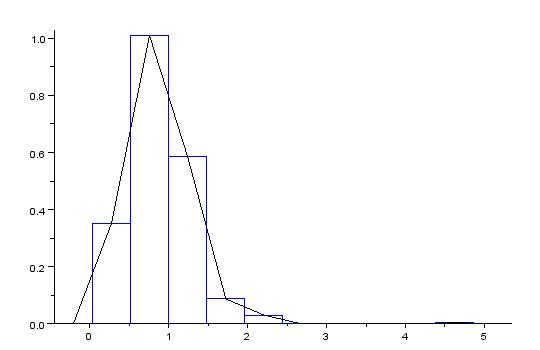
Гистограмма выборки

Найдём функцию, обратную к функции распределения: \\\ скинешь.

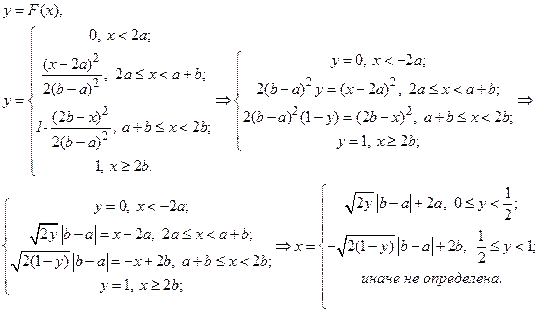
Таким образом, .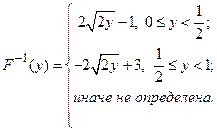

Допустим, что мы имеем случайную величина 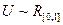. Тогда можно смоделировать случайную величину X как функцию от случайной величины U, обратную функции распределения случайной величины X: 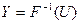. Пронаблюдав эту величину n раз, получим выборку объёма n.

Итак, мы имеем выборку объёма n 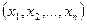, полученную при n наблюдениях за случайной величиной X. Требуется построить гистограмму распределения по этой выборке.

Воспользуемся алгоритмом из первого пункта.

Получаем:
x_min= 0.0310300 x_max= 4.862974

k=10 ∆= 0.4831944

Номер интервала	Интервал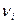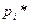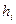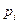
	[-0.9579396; -0.5791479)		0.025	0.0659993	0.068188
	[-0.5791479; -0.2003562)		0.05	0.1319987	0.168478
	[-0.2003562; 0.1784354)		0.08	0.2111979	0.336413
	[0.1784354; 0.5572271)		0.16	0.4223958	0.4375486
	[0.5572271; 0.9360188)		0.175	0.4619954	0.5042029
	[0.9360188; 1.3148105)		0.175	0.4619954	0.4686463
	[1.3148105; 1.6936021)		0.1375	0.3629964	0.3739484
	[1.6936021; 2.0723938)		0.0925	0.2441976	0.2792505
	[2.0723938; 2.4511855)		0.075	0.1979980	0.1845526
	[2.4511855; 2.8299772]		0.03	0.0791992	0.0898547
Σ

Одновременно строим гистограмму выборки и график теоретической плотности вероятностей.