Вопрос 24. Функция распределения и ее свойства

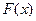(интегральная) называют вероятность того что случайная величина 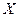примет значения меньше .

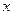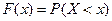(1)

Свойства 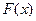(функции распределения случайной величины):

1)

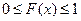
2) неубывающая

Если 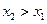, то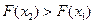

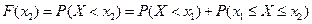
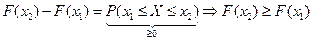
3)

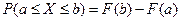
4)

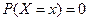
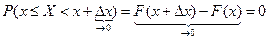
5)

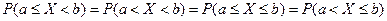
Случайная величина называется непрерывной если непрерывна её функция распределения.

6) Если 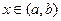, то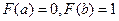

.

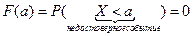
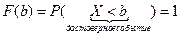Если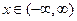

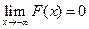
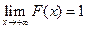
Пример:

Функция распределения для непрерывных случайных величин

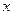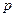	0,2	0,4	0,2	0,2

1)

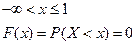
2)

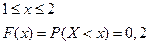
3)

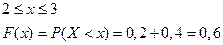
4)

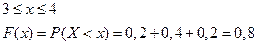
5)

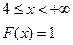
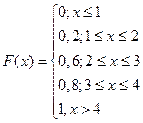
Вопрос 25. Плотность распределения, ее свойства.

Непрерывной случайной величины.

Плотность распределения 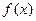или дифференциальная функция – производная от функции распределения .

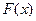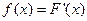
Термин определён для непрерывной случайной величины а не для дискретной.

Свойства :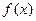

1)

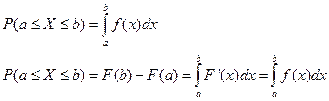
2) 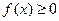, т.к. 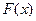неубыв. то 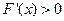или равна 0 в точках экстремума.

3) если случайная величина распределена в промежутке 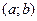то

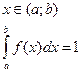по 1му свойству это событие достоверно

4)

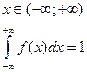
Нахождение 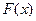по известной плотности.

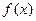известна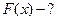

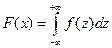(1)

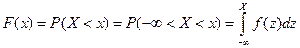
Вопрос 26. Вероятность попадания случайной величины в заданный интервал. Нахождение функции распределения по известной плотности распределения. Вероятностный смысл плотности распределения.

Нахождение 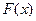по известной плотности.

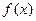известна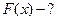

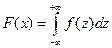(1)

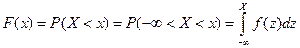
Вероятностный смысл плотности распределения.

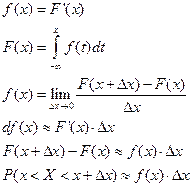
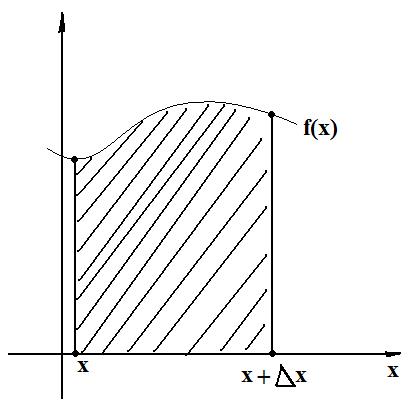
Вероятностный смысл плотности распределения:

Вероятность попадания случайной величины в промежуток 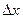приближённо равен произведению плотности распределения вероятности на длину этого промежутка, т.е. площади криволинейной трапеции, ограниченной сверху графиком плотности распределения вероятностей, снизу осью 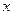, а по бокам прямым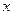и и .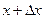

Вопрос 27. Числовые характеристики непрерывной случайной величины.

Числовые характеристики СВ

Исчерпывающие представления о СВ дает закон её распределения.

Во многих задачах, особенно на заключительной стадии, возникает необходимость получить о величине некоторое суммарное представление: центры группирования СВ – среднее значение или математическое ожидание, разброс СВ относительно её центра группирования.

Эти числовые характеристики в сжатой форме отражают существенные особенности изучаемого распределения.

Математическое ожидание (МО)

М(х), МО(х), m_x, m

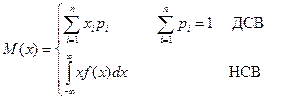
Основные свойства МО:

1. М(х) СВ Х Þ Х_min£М(х)£Х_max

2. М(С)=С МО постоянной величины есть величина постоянная

3. М(Х±У)=М(Х) ±М(У)

4. М(Х×У)=М(х) ×М(у) Þ М(Сх)=СМ(х) – МО произведения двух независимых СВ

5. М(аХ+вУ)=аМ(Х)+вМ(У)

6. М(Х-m)=0 – МО СВ Х от её МО.

МО основных СВ

Дискретные Случайные Величины

1. Биноминальные СВ МО(Х)=np

2. Пуассоновские СВ МО(Х)=l

3. Бернуллиевы СВ МО(Х)=р

4. Равномерно распред. СВ