Дифференциальные уравнения 1 страница
Линейная алгебра
Задание 1.
1.Вычислите определитель 
.
2. Вычислите определитель 
.
3.Вычислите определитель 
.
4. Вычислите определитель 
.
5.Вычислите определитель 
.
6. Вычислите определитель 
.
7.Вычислите определитель 
.
8.Вычислите определитель 
.
9. Вычислите определитель 
.
10. Вычислите определитель 
.
Задание 2.
1. Произведение матриц 
равно…
1) 
; 2) 
; 3) 
; 4) 
.
2. Произведение матриц 
равно…
1) 
; 2) 
; 3) 
; 4) 
.
3. Произведение матриц 
равно…
1) 
; 2) 
; 3) 
; 4) 
.
4. Произведение матриц 
равно…
1) 
; 2) 
;
3) 
; 4) 
.
5. Произведение матриц 
равно…
1) 
; 2) 
; 3) 
; 4) 
.
6. Найдите произведение 
, если 
, 
.
1) 
; 2) не имеет смысла;
3) 
; 4) 
.
7. Найдите произведение 
, если 
, 
.
1) 
; 2) 
; 3) 
; 4) 
.
8. Найдите произведение , если , .
1) ; 2) ; 3) ; 4) .
9. Найдите произведение , если 
, 
.
1) 
; 2) 
; 3) 
; 4) 
.
10. Квадрат матрицы 
равен…
1) 
; 2) 
; 3) 
; 4) 
.
11.Квадрат матрицы 
равен…
1) 
; 2) 
; 3) 
; 4) 
.
12.Квадрат матрицы 
равен…
1) 
; 2) 
; 3) 
; 4) 
.
Задание 3. Решите матричное уравнение:
1. Решением матричного уравнения 
является матрица…
1) 
; 2) 
; 3) 
; 4) 
.
2. Решением матричного уравнения 
является матрица…
1) 
; 2) 
; 3) 
; 4) 
.
3. Решением матричного уравнения 
является матрица…
1) 
; 2) 
; 3) 
; 4) 
.
4. Решением матричного уравнения 
является матрица…
1) 
; 2) 
; 3) 
; 4) 
.
5. Решением матричного уравнения 
является матрица…
1) 
; 2) 
; 3) 
; 4) 
.
6. Решением матричного уравнения 
является матрица…
1) 
; 2) 
; 3) 
; 4) 
.
7. Решением матричного уравнения 
является матрица…
1) 
; 2) 
; 3) 
; 4) 
.
8. Найдите матрицу Х из уравнения 
, если 
, 
.
1) 
; 2) 
; 3) 
; 4) 
.
9. Найдите матрицу Х из уравнения 
, если 
, 
.
1) 
; 2) ; 3) 
; 4) 
.
10.Найдите матрицу Х из уравнения 
, если 
, 
.
1) 
; 2) 
; 3) ; 4) .
Задание 4. Решите систему методом Крамера.
1.Пусть 
– решение системы уравнений 
В ответе укажите 
.
2.Пусть – решение системы уравнений 
В ответе укажите .
3.Пусть 
– решение системы уравнений 
В ответе укажите 
.
4.Пусть – решение системы уравнений 
В ответе укажите .
5.Пусть – решение системы уравнений 
В ответе укажите 
.
6.Пусть – решение системы уравнений 
В ответе укажите 
.
7.Пусть 
– решение системы уравнений 
В ответе укажите 
.
8.Пусть 
– решение системы уравнений 
В ответе укажите 
.
Задание 7.Найдите определитель выражения:
1. Вычислите 
, если 
.
2. Вычислите 
, если 
.
3.Вычислите 
, если 
.
4. Вычислите , если 
.
5. Вычислите 
, если 
.
6.Вычислите 
, если 
, 
.
7. Вычислите 
, если 
, 
.
8. Вычислите 
, если 
, 
.
9.Вычислите 
, если 
, 
.
10. Вычислите 
, если 
, 
.
11. Вычислите 
, если 
, 
– единичная матрица 3–го порядка.
12. Вычислите 
, если 
, – единичная матрица 3–го порядка.
Векторная алгебра
Задание 1.
1. Даны точки 
и 
, причём 
. Найдите значение 
.
2. Даны точки 
и 
, причём 
. Найдите значение 
.
3.Даны точки 
и 
, причём 
. Найдите значение .
4.Даны точки 
и 
, причём 
. Найдите значение 
.
5. Даны точки 
и 
, причём 
. Найдите значение .
6. Даны точки 
и 
, причём 
. Найдите значение 
.
7. Даны точки 
и 
, причём 
. Найдите значение .
Задание 2.
1.Найдите значение «т», при котором векторы 
и 
ортогональны.
2.Найдите значение «т», при котором векторы 
и 
перпендикулярны.
3.Найдите значение «т», при котором векторы 
и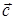 
взаимно перпендикулярны, если 
, 
, 
.
4. Найдите значение «т», при котором векторы 
и 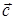взаимно перпендикулярны, если 
, 
, 
.
5. Найдите значение «т», при котором векторы 
и 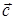взаимно перпендикулярны, если 
, 
, 
.
6.Найдите значение «т», при котором векторы 
и 
ортогональны, если 
, 
, 
.
7.Найдите значение «т», при котором векторы и 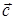ортогональны, если 
, 
, 
.
8. Найдите значение «т», при котором векторы 
и 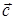взаимно перпендикулярны, если 
, 
, 
.
Задание 3. Найдите скалярное произведение 
, если векторы 
и 
изображены на рисунке:
1. 2.
3. 4.
5. 6.
Задание 4.
1. Найдите значение t, если 
, где 
.