Примеры задач, приводящих к необходимости подсчета числа размещений

1) Сколькими способами можно выбрать из 15 человек 5 кандидатов и назначить их на 5 различных должностей?

2) Сколькими способами можно из 20 книг отобрать 12 и расставить их в ряд на полке?

В задачах о размещениях полагается k < n. В случае, если k = n, то легко получить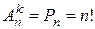

Для подсчета 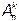используем тот же метод, что использовался для подсчета P_n, только здесь возьмем лишь k ячеек. Первую ячейку можно заполнить n способами, вторую, при заполненной первой, можно заполнить n–1 способами. Таким образом, существует п(п – 1) вариантов заполнения первых двух ячеек. Можно продолжать этот процесс до заполнения последней k–й ячейки. Эту ячейку при заполненных первых k – 1 ячейках можно заполнить n–(k–1) (или n–k+1) способами. Таким образом, все k ячеек заполняются числом способов, равным

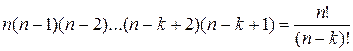
Отсюда получаем: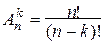

Пример. Сколько существует различных вариантов выбора 4-х кандидатур из 9-ти специалистов для поездки в 4 различных страны?

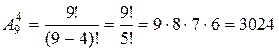
Сочетаниями из n элементов по k элементов называются подмножества, состоящие из k элементов множества 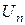(множества, состоящего из n элементов).

Одно сочетание от другого отличается только составом выбранных элементов (но не порядком их расположения, как у размещений).

Число сочетаний из n элементов по k элементов обозначается 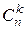(читается "C из n по k").

Примеры задач, приводящих к подсчету числа сочетаний:

1) Сколько существует вариантов выбора 6-ти человек из 15 кандидатов для назначения на работу в одинаковых должностях?

2) Сколькими способами можно из 20 книг отобрать 12 книг?

Выведем формулу для подсчета числа сочетаний. Пусть имеется множество 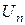и нужно образовать упорядоченное подмножество множества 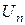, содержащее k элементов (то есть образовать размещение). Делаем это так:

1) выделим какие-либо k элементов из n элементов множества 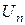Это, согласно сказанному выше, можно сделать 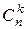способами;

2) упорядочим выделенные k элементов, что можно сделать 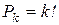способами. Всего можно получить 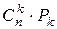вариантов (упорядоченных подмножеств), откуда следует: 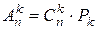, то есть

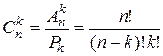(1)

Пример: 6 человек из 15 можно выбрать числом способов, равным

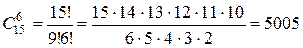
Несложно понять, что осуществить выбор подмножества из т элементов множества, насчитывающего п элементов, можно, выбрав п – т элементов, которые не войдут в интересующее нас подмножество. Отсюда следует свойство числа сочетаний

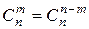
Эту формулу можно доказать, используя формулу (1).

Задачи на подсчет числа подмножеств конечного множества называются комбинаторными.

Рассмотрим некоторые комбинаторные задачи.

1.Из семи заводов организация должна выбрать три для размещения трех различных заказов. Сколькими способами можно разместить заказы?

Так как из условия ясно, что каждый завод может либо получить один заказ, либо не получить ни одного, и что выбрав три завода, можно по-разному разместить среди них заказы, здесь нужно считать число размещений

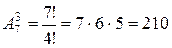
2.Если из текста задачи 1 убрать условие различия трех заказов, сохранив все остальные условия, получим другую задачу. Теперь способ размещения заказов определяется только выбором тройки заводов, так как все эти заводы получат одинаковые заказы, и число вариантов определяется как число сочетаний: .

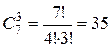3.Имеются 7 заводов. Сколькими способами организация может разместить на них три различных производственных заказа? (Заказ нельзя дробить, то есть распределять его на нескольких заводах).

В отличие от условия первой задачи, здесь организация может отдать все три заказа первому заводу или, например, отдать два заказа второму заводу, а один - седьмому.

Задача решается так. Первый заказ может быть помещен семью различными способами (на первом заводе, на втором и т.д.). Поместив первый заказ, имеем семь вариантов помещения второго (иначе, каждый способ помещения первого заказа может сопровождаться семью способами помещения второго). Таким образом, существует 7×7=49 способов размещения первых двух заказов. Разместив их каким-либо образом, можем найти 7 вариантов помещения третьего (иначе, каждый способ размещения первых двух заказов может сопровождаться семью различными способами помещения третьего заказа). Следовательно, существуют 49×7=7³ способов размещения трех заказов. (Если бы заказов было n, то получилось бы 7ⁿ способов размещения).

4.Как решать задачу 3, если в ее тексте вместо слов "различных производственных заказа" поставить "одинаковых производственных заказа"? Это трудная задача. Ниже приводится аналогичная задача– Задача V с решением.

5.Добавим к условию задачи 1 одну фразу: организация также должна распределить три различных заказа на изготовление деревянных перекрытий среди 4-х лесопилок. Сколькими способами могут быть распределены все заказы?

Каждый из 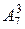способов распределения заказов на заводах может сопровождаться 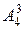способами размещения заказов на лесопилках. Общее число возможных способов размещения всех заказов будет равно

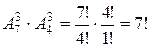
6. Риэлтерская фирма предлагает на продажу 5 больших квартир и 4 малогабаритных квартиры. Банк намеревается купить 4квартиры, причём среди них не должно быть более двух малогабаритных. Сколько вариантов выбора имеет банк?

Банк может купить 4 большие квартиры. У него есть возможность выбрать 4 из 5-ти предлагаемых квартир, и число вариантов здесь равно 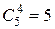. Если банк решит купить три большие квартиры и одну малогабаритную, то число вариантов выбора у него будет равно 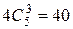. Если будет принято решение купить две малогабаритных квартиры и две больших квартиры, то число вариантов будет равным 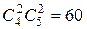. Таким образом, у банка есть 105 вариантов выбора.