Алгебраические критерии устойчивости

Существующие критерии устойчивости можно разделить на алгебраические и частотные. К алгебраическим относятся критерии Рауса-Гурвица, Льенара-Шипара, Вышнеградского. К частотным – критерии Михайлова, Найквиста. Все они названы по фамилиям их авторов. Все критерии устойчивости с математической точки зрения эквивалентны. На практике при исследовании устойчивости выбор критерия определяется удобством его применения для конкретных систем автоматического управления.

Ø Критерий Рауса-Гурвица

Алгебраические критерии устойчивости применяются в случае, когда известны значения или выражения для коэффициентов характеристического полинома САУ:

(7.5)

В конце XIX века учеными Раусом и Гурвицем независимо друг от друга были предложены неравенства, выполнение которых является необходимым и достаточным условием устойчивости систем с характеристическим полиномом любого порядка.

Гурвиц предложил определять устойчивость по специально составленному определителю, элементами которого являются коэффициенты характеристического полинома. Определитель Гурвица составляется по следующей схеме. По главной диагонали последовательно записываются все коэффициенты характеристического полинома от аn–1до а0. Строки влево от главной диагонали дополняются коэффициентами с последовательно убывающими индексами, а вправо – с последовательно возрастающими. Вместо коэффициентов с индексами меньше 0 и больше n записываются нули. В результате определитель имеет следующий вид:

(7.6)

Критерий Гурвица формулируется следующим образом. Для того чтобы САУ была устойчива, необходимо и достаточно, чтобы при положительных коэффициентах характеристического полинома определитель Гурвица и все его диагональные миноры были положительны. Диагональные миноры (определители) отмечены в (7.6) пунктирными линиями.

Раус предложил определять устойчивость по значениям коэффициентов специально составленной таблицы 7.1.

Рассмотрим алгоритм, по которому заполняется специальная таблица с использованием коэффициентов характеристического уравнения:

1) в первой строке записываются коэффициенты уравнения с четными индексами в порядке их возрастания;

2) во второй строке - с нечетными;

3) остальные элементы таблицы определяется по формуле: , где 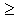3 - номер строки, k - номер столбца.

4) Число строк таблицы Рауса на единицу больше порядка характеристического уравнения.

Для того, чтобы найти k-й коэффициент i­‑го ряда таблицы cki, нужно из (k+1)-го коэффициента (i–2)-й строки (ck+1,i–2) вычесть произведение ri–1на (k+1)-й коэффициент (i–1)-й строки (ck+1,i–1). Множитель ri–1есть отношение первого коэффициента (i–2)‑й строки (c1,i–2) к первому коэффициенту (i–1)-й строки (c1,i–1), постоянный для каждой i-й строки.

Таблица 7.1 - Таблица Рауса

Критерий Рауса формулируется следующим образом. Для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы при положительных коэффициентах характеристического полинома все коэффициенты первой графы таблицы Рауса были положительны, т.е: an> 0, an–1> 0, c13> 0, c14> 0…

Часто критерии Рауса и Гурвица не разделяют, так как они по сути представляют одно и то же. Так, вычисление значений определителей Гурвица наиболее рационально проводить путем приведения их к диагональной форме. При этом элементами такого определителя становятся коэффициенты таблицы Рауса.

Ø Критерий Гурвица

Этот критерий позволяет определить устойчивость САУ, если характеристическое уравнение замкнутой системы представлено в виде:

Для этого строится главный определитель Гурвица по следующему правилу:

- по главной диагонали выписываются все коэффициенты от а1 до аn в порядке возрастания коэффициентов.

- столбцы вверх от главной диагонали заполняются коэффициентами характеристического уравнения с последовательно возрастающими индексами, а столбцы вниз – коэффициентами с последовательно убывающими индексами.

- на месте коэффициентов с индексами, большими порядка характеристического уравнения и меньшими нуля, проставляют нули.

Выделяя в главном определителе Гурвица диагональные миноры, получаем определитель Гурвица низшего порядка. Номер определителя Гурвица определяется номером коэффициента по диагонали, до которого составляют данный определитель.

В критерии устойчивости Гурвица также рассматривается полином 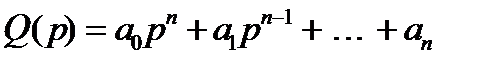. В этом полиноме полагаем 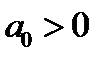. Составим из коэффициентов многочлена определитель:

.

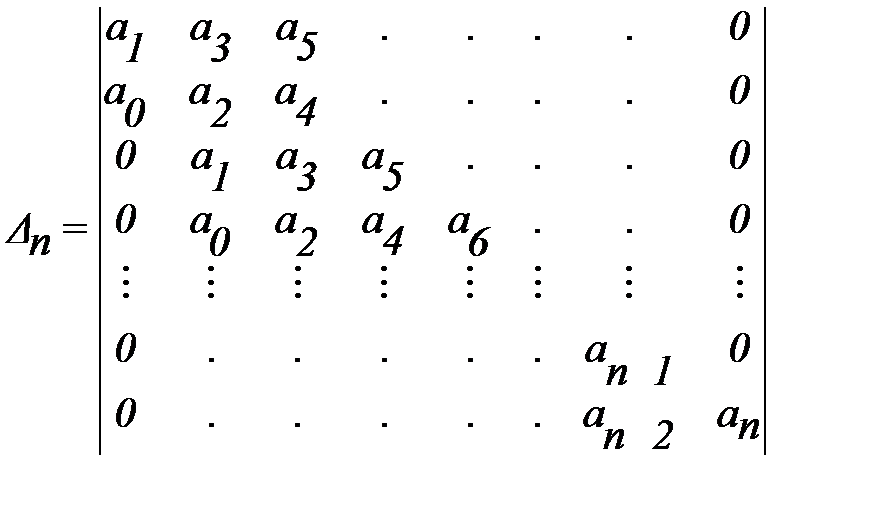Условие устойчивости:

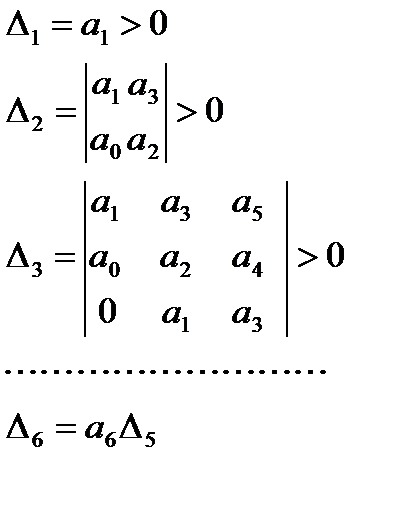
Так как все коэффициенты должны быть положительными и 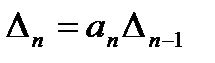, то условие устойчивости записывается в виде: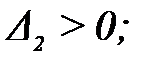

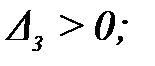
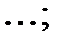
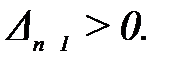
Критерии устойчивости Рауса-Гурвица формулируют следующим образом: для устойчивости замкнутой САУ необходимо и достаточно, чтобы все определители Гурвица были положительны. Таким образом, САУ устойчива, если an > 0 при выполнении следующих условий:

D1 > 0; D2 > 0; D3 > 0; …, Dn > 0.

Раскрыв определители Гурвица, получают условия устойчивости, которые для САУ первого – пятого порядков представлены в таблице 7.1

Таблица 7.1 – Условия устойчивости САУ
Характеристическое уравнение САУ	Условия устойчивости САУ
	,

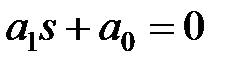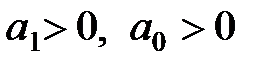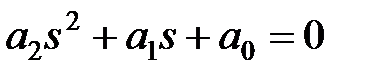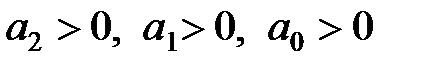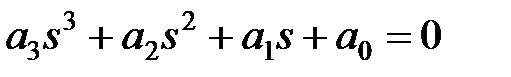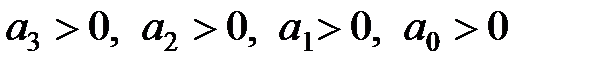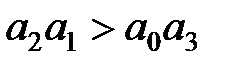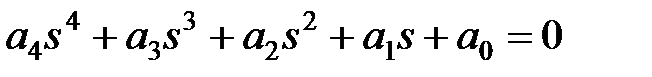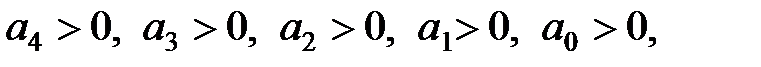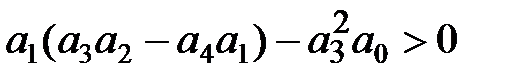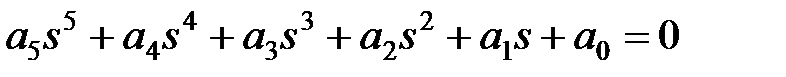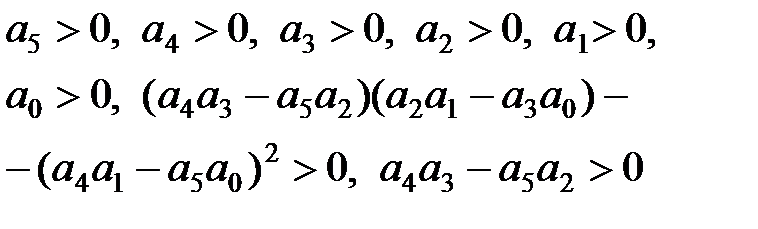Для уравнений первой и второй степеней необходимый критерий устойчивости, заключающийся в требовании положительности всех коэффициентов характеристического уравнения, является и достаточным. Для уравнений более высокого порядка положительность коэффициентов характеристического уравнения является необходимым, но недостаточ­ным условием устойчивости. Например, необходимые и достаточные условия устойчивости для уравнения третьей степени включают кроме требования положительности четырех коэффициентов характеристичес­кого уравнения дополнительное пятое условие 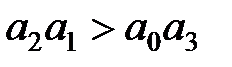. Условия устойчивости усложняются с ростом порядка системы.

Определение: чтобы САУ была устойчива, необходимо и достаточно, чтобы определитель Гурвица и его диагональные миноры имели знаки, одинаковые со знаком первого коэффициента характеристического уравнения замкнутой САУ.

Линейная система устойчива, если при выполнении необходимого условия (8.6), определитель Гурвица и все его диагональные миноры будут положительны:

Δ₁ > 0, Δ₂ > 0, …………,Δ_n > 0.

Рассмотрим примеры применения критерия Гурвица:

1) n = 1 => уравнение динамики: a₀p + a₁ = 0. Определитель Гурвица: 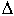= 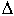₁ = a₁ > 0 при a₀ > 0, то есть условиие устойчивости: a₀> 0, a₁ > 0;

2) n = 2 => уравнение динамики: a₀p² + a₁p + a₂ = 0. Определители Гурвица: 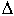₁ = a₁> 0, D₂ = a₁a₂ - a₀a₃ = a₁a₂ > 0, так как a₃ = 0, то есть условие устойчивости: a₀> 0, a₁> 0, a₂ > 0;

3) n = 3 =>уравнениединамики: a₀p³ + a₁p² + a₂p + a₃ = 0. ОпределителиГурвица: 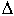₁ = a₁> 0, 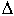₂ = a₁a₂ - a₀a₃ > 0, 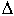3 = a_{3 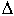2} > 0, условиеустойчивости: a₀ > 0, a₁ > 0, a₂ > 0, a₃ > 0, a₁a₂ - a₀a₃ > 0;

Таким образом при n 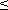2 положительность коэффициентов характеристического уравнения является необходимым и достаточным условием устойчивости САУ. При n > 2 появляются дополнительные условия.

Критерий Гурвица применяют при n 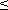4. При больших порядках возрастает число определителей и процесс становится трудоемким. Имеется ряд модификаций данного критерия, расширяющие его возможности.