Элементы функционального анализа

Введенные ранее абстрактные понятия приобретают свое конкретное выражение в частных случаях топологических пространств - метрических и нормированных. Для конечномерных пространств эти вопросы рассмотрены вне связи с топологическими понятиями в приложении 1. Здесь основным предметом рассмотрений пространства, элементами которых служат функции и другие, более общие объекты.

Качественно, метрика - это формализованное понятие расстояния между двумя объектами заданного множества, и если это понятие, подчиненное ряду требований, определено над линейным векторным пространством, то последнее превращается в метрическое пространство. Поскольку с введением понятия расстояния автоматически определяются и окрестности того либо иного элемента, то метрическое пространство оказывается и топологическим. Обратное, вообще, говоря, неверно. Не всякое топологическое пространство является метрическим. Иными словами, не всякая топология, т.е. базис окрестностей, определяется метрикой. Если в конечномерном случае это различие в основном терминологическое, то в бесконечномерном – пространстве отображений: функций, функционалов, операторов это различие весьма существенно и имеет значимые конструктивные следствия. Аналогично понятие нормы является более жестким, чем понятие метрика. Всякая норма есть одновременно и метрика, но не всякая метрика – норма.

Понятие метрики играет существенную роль в постановках и решении обратных задач геофизики. Действительно, при решении обратной задачи необходимо как можно лучше, точнее приблизить рассчитанное от того, либо иного, элемента поле к наблюдаемому. Именно наилучшее совпадение рассчитанного и наблюдаемого полей и является одним из основных критериев отбора решения. Но для такого сравнения необходимо уметь вычислять величину уклонения одного поля от другого, причем для того, чтобы результаты вычислений можно было всегда сравнить, ими – результатами, должно быть упорядочено множество, например, вещественные числа (а не комплексное или вектор). Способов такого расчета может быть много. Все зависит от тех факторов, которые следует принимать во внимание. 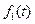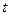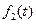Например, расстояние функции переменной от можно оценить величинами:

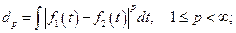
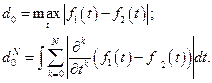
Все они с формально математической стороны равноправны, но при этом выражают различные принципы близости двух элементов, и, как следствие, приводят к различным результатам при решениям обратных задач. Приведенные примеры - это примеры задания норм и, как следствие, метрик различным способом на одном и том же пространстве состоящем из функций 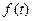одного переменного, обозначенного 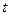и имеющих некоторую естественную область определения, по которой осуществляется интегрирование или нахождение максимума. Дадим теперь несколько более точных определений.

Метрическим пространствомназывается пара 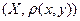, состоящая из множества Х и функции 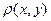, определенной на 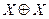, называемой метрикой, удовлетворяющая условиям:

1) 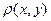определена для всех 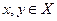и принимает только неотрицательные значения из множества вещественных чисел ;

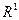2) 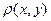=0 тогда и только тогда, когда ;

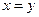3) ;

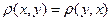4) .

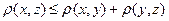Линейная система, снабженная метрикой, называется линейным метрическим пространством.

Если в качестве х положим 0 (при условии 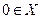), то 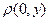характеризует уклонение 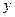от нуля.

Если - линейная система, и для каждого 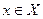определена вещественно-значная функция 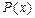, удовлетворяющая условиям:

1) ;

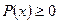2) 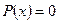только при ;

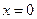3) 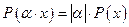для всех , где – вещественное либо комплексное число;

4)

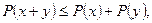
то 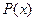называется нормойэлемента , а линейная система, снабженная нормой - линейным нормированным пространством.

Обратите внимание на отличие нормы и метрики. Оно состоит в более жестком условии на норму - условии (3), аналог которого отсутствует у метрики.

Поскольку в дальнейшем мы будем иметь дело исключительно с линейными системами, то вместо «линейное нормированное (метрическое) пространство» будем писать просто «нормированное (метрическое) пространство». Всякое нормированное пространство является одновременно и метрическим, где метрика 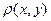определена условием:

.

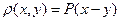Норму элемента х будем обозначать 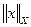, опуская индекс , уточняющий вид нормы там, где это не приведет к недоразумениям (т.е. когда очевидно, какое конкретно пространство имеется в виду или, что то же самое, каким конкретно выражением определена функция 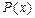). В главном нас будут интересовать нормированные пространства.

Понятно, что и метрические и, тем более, нормированные пространства, являются топологическими линейными пространствами. В качестве топологии в нормированном пространстве выступают открытые множества 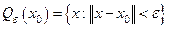, которые называются 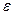- окрестностью точки 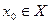. Замыкание 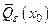окрестности 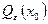есть множество

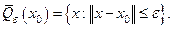
Пусть 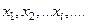- последовательность элементов в метрическом пространстве Х. Говорят, что эта последовательность сходитсяк 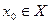, если всякая окрестность 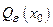для любого 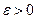содержит все точки х_n, начиная с некоторого номера .

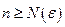Эквивалентное определение: последовательность 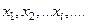сходится в точке 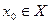, если

.

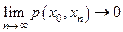Для нормированных пространств это условие таково:

.

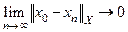Последовательность точек 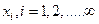метрического (нормированного) пространства Х называется фундаментальной, если для любого 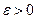существует 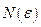, и 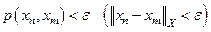для всех 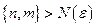. Если последовательность 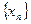сходится, то она фундаментальна. Если же в пространстве Х (метрическом или нормированном) любая фундаментальная последовательность сходится, то пространство называется полным.

Операция замыкания множествасостоит в присоединении к нему пределов всех фундаментальных последовательностей.

Понятие плотного множества, введенное в топологическом пространстве, в метрических пространствах формулируется на языке сходимостей или замыканий. Если 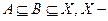метрическое пространство и 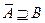, то А плотно в В.

Операция присоединения к линейному метрическому пространству пределов всех его фундаментальных последовательностей называется пополнением пространства. Отличие от замыкания состоит в том, что пополнение – операция, относящаяся ко всему метрическому пространству, а замыкания – только к его подмножеству.

Полное нормированное пространствоназывается банаховым (пространства Банаха). Банаховы пространства могут получены из нормированных путем их пополнения.

Теорема Бэра-Хаусдофа. Всякое непустое полное метрическое пространство является множеством второй категории.

Поскольку объединение счетного числа множеств первой категории есть снова множество первой категории, то из приведенной теоремы следует, что банахово пространство не может быть получено как объединение счетного числа множеств первой категории.

Для многих вопросов важным является понятие компактности. Общее определение таково, пригодное для более общих, чем нормированные, линейных топологических пространств:

Топологическое пространство называется компактным, если любое его открытое покрытие содержит конечное подпокрытие. Если рассматриваемое пространство хаусдорфово, т.е. две его различные точки имеют непересекающиеся окрестности, то компактное пространство (множество) называется компактом. Это определение эквивалентно важнейшему свойству компактов, из-за которых нас они и интересуют. Оно состоит в том, что:

Компактное множестваявляется замкнутым, и всякое его бесконечное подмножество имеет хотя бы одну предельную точку. Всякое замкнутое подмножество компактного множества компактно, и непрерывный образ компактного множества компактен.

Следующая теорема очень часто используется.

Теорема о гомеоморфизме. Взаимнооднозначное и непрерывное отображение компакта на хаусдорфо пространство есть гомеоморфизм.

Значение приведенного результата состоит в том, что им гарантируется непрерывность обратного к 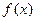отображения 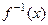, определенного на образе 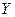компакта ; 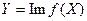, если 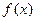– взаимнооднозначен и непрерывен из в 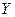. Иными словами, из взаимной однозначности, непрерывности «туда» следует и непрерывность «обратно». Непрерывность как понятие определено через топологию и зависит от ее вида.

В геофизических приложениях, при рассмотрении обратных задач, непрерывность обратного преобразования обеспечивает теоретическую устойчивость определения параметров среды – элемента из X, как функции наблюдаемой - элемента из Y, если 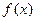- непрерывное отображение модели среды в модель поля. Использование компактных множеств важно и для задач минимизации, поскольку их введением обеспечивается существование решения соответствующей задачи. Точнее, справедлив такой результат.

Следствие. Пусть Х - компактное множество и 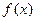непрерывная на Х числовая функция. Тогда 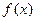ограничена на Х и достигает на Х верхней и нижней грани.

Свойством несколько более слабым, чем компактность, является счетная компактность.

Топологическое пространство Х называется счетно-компактным, если любое его открытое счетное покрытие имеет конечное подпокрытие. Эквивалентное определение таково: топологическое пространство называется счетно-компактным, если любое его бесконечное подмножество имеет хотя бы одну предельную точку.

В метрических пространствах, как следствие и нормированных, понятия счетной компактности и компактности совпадают.

Предкомпактным(иногда в литературе употребляют термин «относительно компактным») называется множество, замыкание которого компактно.

Пространство называется локально-компактным, если каждая его точка имеет предкомпактную окрестность.

В нормальном (отделимом) линейном пространстве все замкнутые ограниченные множества компактны тогда и только тогда, когда пространство конечномерно. Отсюда следует, что в конечномерных пространствах понятие компактности сводится к ограниченности и замкнутости. Но тогда по теореме о гомеоморфизме:

всякое однозначное непрерывное отображение 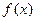конечномерного пространства , определенное на замкнутом ограниченном множестве 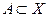имеет ограниченное обратное на образе 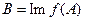этого множества.

Рассмотрим теперь более частные случаи отображений.

Пусть Х,Y – линейные топологические пространства и 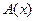преобразование из Х в Y. Преобразование 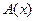называется аддитивным, если:

.

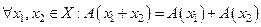Аддитивное преобразование, непрерывное в одной какой-нибудь точке, непрерывно всюду. Если преобразование аддитивно и однородно, т.е. 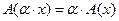, где α скаляр, то, 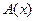называется линейным преобразованием. Из определения следует, что линейное преобразование должно быть определено на линейном пространстве.

Если преобразование 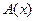отображает ограниченные множества в ограниченные, то оно называется ограниченным.

Для линейных преобразований, действующих из нормированного пространства Х в нормированное пространство Y , понятия ограниченности и непрерывности совпадают.

Для линейного непрерывного преобразования, действующего в паре банаховых пространств (из Х в Y) вводится его норма:

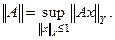
Из ее определения следует неравенство:

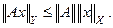
Ограниченность линейного преобразования 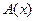эквивалента требованию: .

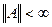Преобразования в произвольных топологических пространствах Х и Y называются операторами, а в том частном случае, когда Y – множество вещественных, либо комплексных чисел, А называется вещественно-значным, либо комплексно-значным функционалом. В дальнейшем используются исключительно вещественно-значные функционалы, поэтому прилагательное вещественно-значный будет опущено.

Наряду с введенными обозначениями для области определения 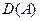, области значений 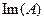произвольного оператора для линейного оператора дополнительно вводится понятие ядра оператора: .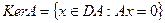

Если А - линейный ограниченный оператор из банахова пространства Х в банахово пространство Y, то КerA - замкнутое линейное подпространство в Х.

Понятие ядра по аналогии можно ввести и для нелинейного оператора, но оно не будет иметь столь широкого применения, как для линейного, уже лишь потому, что не будет являться линейным подпространством в Х, как это имеет место для линейного случая.

Пусть Х - банахово пространство. Совокупность всех линейных ограниченных функционалов, определенных на Х, обозначается Х* и называется сопряженным пространствомк X. Элементы 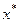из Х^* представляют собой отображения 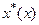из во множество вещественных чисел, и для этого отображения вводится, в силу его особой значимости, специальное обозначение: 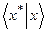. По причинам, которые станут ясны из дальнейшего, элементы из Х^* иногда будем отождествлять с х^*, входящим в выражение .

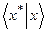Из приведенных выше общих сведений, следует, что Х^* является линейным нормированным пространством с нормой:

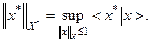(2.1)

Равенство (1) может быть обращено:

(1.2)

Последнее соотношение можно рассматривать как определение нормы при заданном виде сопряженного пространства, а соотношение (1) - как определение нормы в сопряженном пространстве при заданном исходном.

Если Х - банахово пространство, то Х^* относительно нормы (1) тоже банахово. Чаще всего Х - это пространство функций некоторого переменного, например, τ : х(τ). Выбор переменной, как и ее размерность, не имеет значения. Важно, что эта переменная определена в некоторой области . В этих и аналогичных им случаях справедлива теорема Риссаоб общем виде линейного ограниченного функционалана пространстве Х. В соответствии с этой теоремой, каждый элемент из Х^* отождествляется с некоторым интегралом:

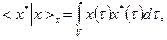
где элемент х^*(τ) принадлежит некоторому другому функциональному пространству, называемому двойственным к . Благодаря этому интегралу двойственное пространство, 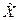, состоящее из функций х^*(τ), находится в соответствии и отождествляется с 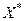. Справедливо и обратное - каждый такой интеграл с заданной функцией х^*(τ) из 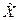порождает линейный непрерывный функционал на Х и представляет собой элемент из 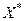. Норма отображения 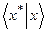в соответствии с определением (1) оказывается равной норме элемента 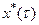в пространстве 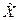двойственном к Х. Таким образом, 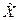и Х^* находятся во взаимнооднозначном соответствии и поэтому отождествляются. Вместо 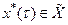записываем 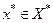и в этом смысле говорим, что Х^* двойственно Х.

Если Х - банахово пространство, то пространство Х^* также линейно и нормированно. Следовательно, можно построить и к нему сопряженное, которое называется вторым сопряженным к Х и обозначается Х^**. Понятно, что 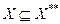. В том частном случае, когда 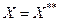^*, Х называется рефлексивным.

Топологию банахова пространства Х, порожденную нормой, называют сильной. Соответственно, говорят о сильной сходимости, сильных пределах, сильном замыкании, сильной компактности и т.д., когда хотят подчеркнуть, что речь идет о топологии нормы.

Исходя из заданной системы функционалов над Х, может быть определена другая топология, зависящая от того, какие функционалы считаются непрерывными.

Слабейшая из всех топологий на Х, относительно которой непрерывны все функционалы из Х^*, называется слабой топологией. Соответственно, возникает понятие слабой полноты, слабой компактности, слабой замкнутости, слабой сходимости, слабой непрерывности и т.д.

Приведем сведения о некоторых свойствах слабой топологии и ее соотношения с сильной.

Слабая топология на Х слабее, чем сильная так, что всякая сильно сходящаяся последовательность является и слабо сходящейся, и всякое сильно непрерывное отображение - слабонепрерывным. Обратное, вообще говоря, неверно. Слабо сходящаяся последовательность может не иметь сильного предела. Это практически очень значимое обстоятельство. Отсюда, в частности, следует, что слабое замыкание некоторого множества шире, чем его сильное замыкание.

Рассмотрим такой пример. Пусть L₂ (-π,π) обозначает множество функций, определенных на интервале (-π, π) и имеющих конечную величину квадратичной Гильбертовой нормы:

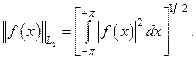
Сопряженное к 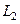в приведенном выше смысле совпадает с самим 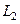. Точнее говоря двойственным к 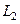служит само 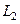и, следовательно, сопряженное к 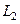отождествляется с самим 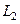(это следует из неравенства Гельдера - см. п. 5 настоящего приложения). В этом случае, в соответствии с теоремой Риса:

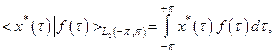
где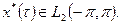

Таким образом:

.

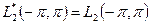Рассмотрим последовательность функций 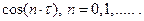Она не является сильно сходящейся, но из теории рядов Фурье известно, что для любой квадратичной интегрируемой функции :

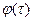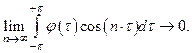
Это означает, что последовательность 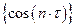сходится слабо к нулю, ибо для каждого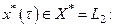

.

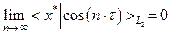Однако из слабой сходимости последовательности следует, что она ограничена. Точнее, если последовательность 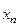сходится слабо, то:

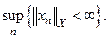
Любое сильно замкнутое подпространство слабо замкнуто и всякое сильно замкнутое выпуклое множество является слабо замкнутым. Верно и обратное. Слабо замкнутое выпуклое множество одновременно и сильно замкнуто. Таким образом, для выпуклых множеств понятия сильной и слабой замкнутости совпадают.

Слабо компактное множество слабо полно.

Если последовательность 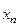слабо сходится к 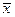, то для любого целого положительного n и любого ε > 0 можно указать такое конечное множество действительных чисел 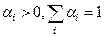, что .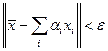

Этот результат означает, что из слабо сходящейся последовательности можно построить выпуклую комбинацию ее элементов, сходящуюся сильно.

На пространстве Х^* наряду с сильной топологией, определенной нормой:

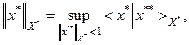
может быть введена и слабая топология. Но больший интерес представляет другая, родственная ей топология, называемая *- слабой.

* - слабая топологияна Х^* - это слабейшая из всех топологий, в которых непрерывны функционалы 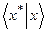на Х^* при 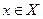(а не 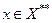). Эта топология совпадает со слабой топологией на Х^*, если Х=Х^**. Последнее имеет место, когда Х – рефлексивно. Таким образом, введение понятия *- слабой топологии, в отличие от слабой, содержательно только для нерефлексивных пространств. Поскольку в этих случаях 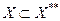, то *- слабая топология слабее, чем слабая топология на Х^*.

К числу нерефлексивных пространств относятся пространства непрерывных и пространства абсолютно интегрируемых функций. * - слабая топология потребуется при рассмотрении задач на минимум, именно в этих пространствах, и в этой связи важен результат:

Теорема Банаха-Алаоглу*. Сфера S в 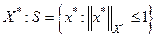компактна в * - слабой топологии пространства Х^*.

Поскольку в рефлексивном пространстве Х=Х^**, то из приведенной теоремы вытекает следующий результат.

Следствие 1. В рефлексивном пространстве сфера 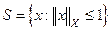слабо компактна.

Оказывается справедливо и обратное.

Следствие 2. Если сфера 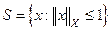слабо компактна, то пространство Х рефлексивно.

Слабая топология может совпадать с топологией нормы (сильной). Для этого необходимо и достаточно, чтобы Х было конечномерно.

Если М - некоторое подмножество в линейном топологическом пространстве Х, то совокупность элементов х^* из Х^*, таких, что 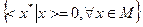, называется аннулятором М и обозначается 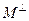. Если М дополнительно является линейным подпространством, то 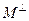называется ортогональным дополнениемк М, и есть линейное подпространство в Х^*, замкнутое относительно сильной топологии в Х^*.

Операторы.

Пусть Х - линейное топологическое пространство и Х₁- его подпространство. Пусть, далее А₁ - линейный оператор, определенный на Х₁, и А – оператор, определенный на Х. Если: 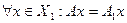, то А называется расширением 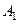. Соответственно 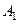– сужение Ас Х на .

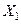Пусть А есть линейный оператор, действующий из банахова пространства Х в банахово пространство Y (А: Х→Y). Рассмотрим множество G, образованное прямым произведением области определения (множества D(A)) и области значений (множества ImA) оператора А. Множество G называется графиком оператораи состоит из всевозможных пар (х,у)=(х,Ах). Это множество называется графиком оператора А. Введя норму для элемента из 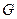правилом 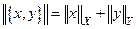, превращаем G в нормированное пространство. Если во введенной норме график операторов А оказывается замкнутым множеством, то оператор А называется замкнутым. Иными словами, оператор А замкнут, если из условий 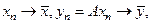следует что 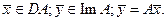Здесь важно иметь в виду, что замкнутость А не означает сходимость у_n из сходимости х_n , что имеет место для ограниченных операторов. 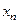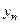Замкнутость означает, что из сходимости последовательностей и следует, что пара 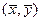– их предел, принадлежит графику.

Непосредственно из определения следует, что если А – замкнут и имеет обратный, то А^-1 также замкнут.

Практически возникающие при рассмотрении интерпретационных задач в геофизике операторы всегда замкнуты и имеют в качестве области определения некоторое линейное множество – линейное пространство 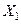. Это множество можно пополнить до некоторого банахова пространства Х (без продолжения оператора на пополнение) и считать, что А имеет область определения, плотную в банаховом пространстве Х. Это далее предполагается.

Множество линейных замкнутых операторов, действующих из банахова пространства Х в банахово пространство Y, обозначается: [Х→Y].

Исключительно важным для дальнейшего является понятие сопряженного оператора. Это одно из центральных понятий, используемых как в теории операторов, так и более узком вопросе, но основном, для рассмотрения в этой книге - теории и методах анализа и решения некорректных задач математической физики.

Пусть А - линейное преобразование, действующие из Х в Y, где Х, Y - банаховы пространства. Как и всюду, далее предполагаем, что DA плотно в Х. Рассмотрим линейный ограниченный функционал 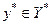на :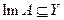

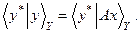
Этот функционал является одновременно и функционалом на элементах из 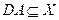, т.е. элементом из Х^* и, следовательно, существует элемент 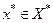такой, что; 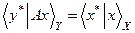. Этот элемент зависит от принятого 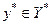и оператора .

Последнее равенство определяет отображение А^* из Y^* в Х^* по правилу:

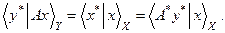
Требование плотности DA в Х необходимо для того, чтобы А^* был однозначен. Оператор А^* называется сопряженнымк А.

Приведем некоторые примеры (используются в 7.1). Пусть А действует из L₂ (V), в R³, в L₂ (E₀) по правилу:

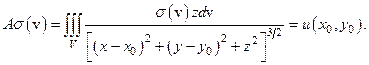(2.2)

Здесь V - замкнутая ограниченная область, 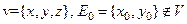. Например, .

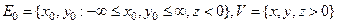Этот оператор соответствует оператору прямой задачи гравиразведки. Он ограничен (см.7.1 из L₂(V) в L₂(E₀)). Тогда, учитывая, что двойственным к L₂ служит само L_2, получим для :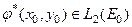

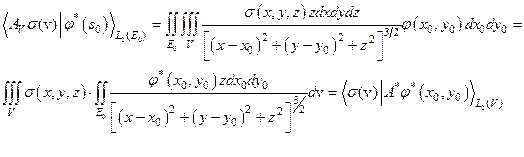
Таким образом, оператор А^* ставит в соответствие элементу 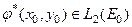элемент[37]:

.

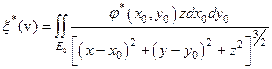Свойства оператора и его сопряженного тесно связаны между собой. Без доказательства укажем следующие из них.

Если А - линеен и задан на плотном в банаховом пространстве Х множестве, то А^*- замкнут, и 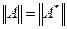. Если дополнительно А имеет обратный, ImA=Y (всюду предполагается, что Х,Y - банаховы пространства), то (А^*)^-1=(А^-1)^*; А^-1 ограничен тогда и только тогда, когда 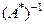ограничен на Х^*.

Операторами, являющимися замкнутыми, исчерпывается большинство геофизических приложений. Поэтому сформулируем основные результаты для этого класса операторов.

Теорема 2. Если А - замкнутое линейное преобразование из Х в Y ( 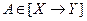), область значений которого 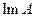- множество второй категории в Y, то

1) ;

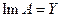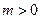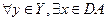2) существует такая постоянная, что и: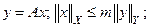

3) если существует обратное преобразование (А – взаимнооднозначен), то оно ограничено.

Отсюда, в частности, следует:

если 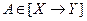, ImA=Y и А – взаимнооднозначен, то ;

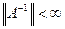если 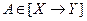и DA есть множество второй категории в Х, то DA=Х, и ;

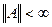если 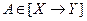и А не ограничен, то DA не может совпадать со всеми Х, а в лучшем случае образует лишь плотное в Х подмножество.

Таким образом, если А - замкнут, взаимнооднозначен, и ImA есть множество первой категории, то А не имеет ограниченного обратного. В этом случае ImA не содержит ни одной внутренней точки (как множество первой категории).

Для оператора (2), который использовался в качестве примера выше, можно доказать, что область его значений есть множество первой категории в 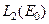при 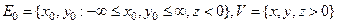. Это сделано в п.7.1. Тогда из приведенной теоремы, в частности, следует вывод, что он не имеет ограниченного обратного.

При рассмотрении обратных задач с замкнутым оператором в паре банаховых пространств:

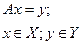(2.3)

Прежде всего, возникают вопросы, связанные с разрешимостью этой задачи.

Уравнение (3) называется:

однозначно разрешимым(о.р.), если ;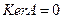

плотноразрешимым (п.р.), если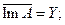

вездеразрешимым(в.р.) при ImA=Y;

корректноразрешимы (к.р.) при .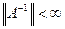

Из приведенных выше результатов следует, что для замкнутого взаимнооднозначного оператора из всюду разрешимости следует корректная разрешимость.