О всех задачах считать СКП пеленга равным ±2°, дистанции – ±0,5 мили.

руппа СВ-311

Счислимые координаты: Широта 44°47,0ʼN, долгота 32°47,0ʼ E

№ вар	Ориентир	ГКП	Д
(1)	М-к Лукул М-к Евпаторийский М-к Херсонес	223,9 285,3	35,3
(2)	М-к Лукул М-к Евпаторийский М-к Херсонес	222,9 284,3	34,3
(3)	М-к Лукул М-к Евпаторийский М-к Херсонес	221,9 283,3	33,3
(4)	М-к Лукул М-к Евпаторийский М-к Херсонес	227,9 289,3	32,3
(5)	М-к Лукул М-к Евпаторийский М-к Херсонес	228,9 290,3	31,3
(6)	М-к Лукул М-к Евпаторийский М-к Херсонес	223,9 286,3	32,3
(7)	М-к Тарханкут М-к Евпаторийский М-к Херсонес	223,9 285,3	33,3
(8)	М-к Лукул М-к Евпаторийский М-к Херсонес	222,9 284,3	34,0
(2)	М-к Лукул М-к Евпаторийский М-к Херсонес	223,9 286,3	35,3
(10)	М-к Лукул М-к Евпаторийский М-к Херсонес	218.1 294.8	42,0
(11)	М-к Лукул М-к Евпаторийский М-к Херсонес	223.9 296.9	43,0
(12)	М-к Лукул М-к Евпаторийский М-к Херсонес	217.9 390.9	44,0
(13)	М-к Лукул М-к Евпаторийский М-к Херсонес	224.1 300.8	45.0
(14)	М-к Лукул М-к Евпаторийский М-к Херсонес	218.1 294.8	46,0
(15)	М-к Лукул М-к Евпаторийский М-к Херсонес	217.5 298.1	34,0
(16)	М-к Лукул М-к Евпаторийский М-к Херсонес	211.5 292.1	35,3
(17)	М-к Тарханкут М-к Евпаторийский М-к Херсонес	227.5 312.0	42,0
(18)	М-к Лукул М-к Евпаторийский М-к Херсонес	221.5 306.0	43,0

руппа СВ-312

Счислимые координаты: Широта 44°23,0ʼN, долгота 35°03,0ʼ E

№ вар	Ориентир	ИП	Д
(19)	М-к Айтадор М-к Меганом М-к Рыбацкий	95.9 185.8	28.3
(21)	М-к Айтадор М-к Меганом М-к Рыбацкий	96.9 186.8	27,0
(22)	М-к Айтадор М-к Меганом М-к Чауда	97.9 187.8	26,0
(23)	М-к Айтадор М-к Меганом М-к Рыбацкий	96.9 186.8	25,0
(24)	М-к Айтадор М-к Меганом М-к Рыбацкий	95.9 185.8
(25)	М-к Айтадор М-к Меганом М-к Рыбацкий	97.9 187.8	35,0
(26)	М-к Айтадор М-к Меганом М-к Рыбацкий	92.3 156.7	36,0
(27)	М-к Айтадор М-к Меганом М-к Рыбацкий	93.3 157.7	37,0
(28)	М-к Айтадор М-к Меганом М-к Рыбацкий	94.3 157.7	38,0
(29)	М-к Айтадор М-к Меганом М-к Рыбацкий	96.9 186.8	28.3
(2)	М-к Айтадор М-к Меганом М-к Рыбацкий	95.9 185.8	27,0
(30)	М-к Айтадор М-к Меганом М-к Рыбацкий	97.9 187.8	26,0
(31)	М-к Айтадор М-к Меганом М-к Рыбацкий	92.3 156.7	25,0
(32)	М-к Айтадор М-к Меганом М-к Рыбацкий	93.3 157.7
(33)	М-к Айтадор М-к Меганом М-к Рыбацкий	94.3 157.7	35,0
(34)	М-к Айтадор М-к Меганом М-к Рыбацкий	97.9 187.8	36,0
(35)	М-к Айтадор М-к Меганом М-к Рыбацкий	96.9 186.8	37,0
(36)	М-к Айтадор М-к Меганом М-к Рыбацкий	95.9 185.8	38,0

руппа СВ-32

Счислимые координаты широта и долгота.

№ вар	Ориентир	ИП	Д	Широта	Долгота
(37)	М-к Анапа М-к Кыз-Аул М-к Железный Рог	228,5 169,0	33,0	44°33,0ʼN	36°33,0ʼ E
(38)	М-к Анапа М-к Кыз-Аул М-к Железный Рог	230,5 168,0	31,9	44°33,0ʼN	36°33,0ʼ E
(39)	М-к Анапа М-к Кыз-Аул М-к Железный Рог	229,5 175,0	31,0	44°33,0ʼN	36°33,0ʼ E
(40)	М-к Анапа М-к Кыз-Аул М-к Железный Рог	232,5 176,0	30,0	44°33,0ʼN	36°33,0ʼ E
(41)	М-к Анапа М-к Кыз-Аул М-к Железный Рог	234,5 169,0	29,0	44°33,0ʼN	36°33,0ʼ E
(42)	М-к Чауда М-к Кыз-Аул М-к Железный Рог	223,5 168,0	40,9	44°23,0ʼN	36°33,0ʼ E
(43)	М-к Анапа М-к Кыз-Аул М-к Железный Рог	222,5 175,0	42,0	44°23,0ʼN	36°33,0ʼ E
(44)	М-к Анапа М-к Кыз-Аул М-к Железный Рог	219,5 176,0	43,0	44°23,0ʼN	36°33,0ʼ E
(45)	М-к Анапа М-к Кыз-Аул М-к Железный Рог	220,5 169,8	44,0	44°23,0ʼN	36°33,0ʼ E
(46)	М-к Анапа М-к Кыз-Аул М-к Железный Рог	219,5 170,8	45,0	44°23,0ʼN	36°33,0ʼ E
(47)	М-к Анапа М-к Кыз-Аул М-к Железный Рог	230,5 171,8	33,0	44°33,0ʼN	36°33,0ʼ E
(48)	М-к Чауда М-к Кыз-Аул М-к Железный Рог	232,3 165,8	31,9	44°33,0ʼN	36°33,0ʼ E
(49)	М-к Анапа М-к Кыз-Аул М-к Железный Рог	233,3 164,8	31,0	44°33,0ʼN	36°33,0ʼ E
(50)	М-к Анапа М-к Кыз-Аул М-к Железный Рог	231,3 163,8	30,0	44°33,0ʼN	36°33,0ʼ E
	М-к Анапа М-к Кыз-Аул М-к Железный Рог	234,3 163,8	29,0	44°33,0ʼN	36°33,0ʼ E
	М-к Анапа М-к Кыз-Аул М-к Железный Рог	224,3 164,8	40,9	44°23,0ʼN	36°33,0ʼ E
	М-к Анапа М-к Кыз-Аул М-к Железный Рог	222,3 165,8	42,0	44°23,0ʼN	36°33,0ʼ E
	М-к Анапа М-к Кыз-Аул М-к Железный Рог	221,5 171,8	43,0	44°23,0ʼN	36°33,0ʼ E

Методические указания

Ответы на выполнение задачи № 5 должны содержать следующие результаты решения своего варианта задачи ОМС с избыточным числом навигационных параметров..

рафически

1.1 Проложили на карте и кальке изолинии и обозначили фигуру погрешности.

1.2 Заменили изолинию дистанции хордой и сняли с карты элементы трех исходных ЛП: Δn_i и τ_i.

рафоаналитически

2.1 Рассчитывают по формулам плоской счислимые значения пеленгов и дистанций, используя координаты ориентиров и счислимой точки.

Для контроля снимают с карты между ориентирами и счислимой точкой величины:

Пс₁ , Dс₁ , Пс₂= , Dс₂ = ; Пс₃ , Dс₃

.

2.2 Рассчитывают градиенты изолиний:

g_П = 57,3°/ Dс₁ = g_D = 1

и направления градиентов:

τ_П = Пс₁ + 90°; τ_D = Пс₂.

2.3 Рассчитывают элементы переносов линий положения (ЛП) по формулам:

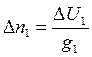= (По-Пс₁)/g _{П = ;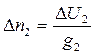} = (Dо-Dс₂)/g_D=

2.4 Построить на обратной стороне бланка астрономических вычислений по направлениям градиентов и величинам переносов все ЛП.

На бланке от счислимой точки по расчетным элементам Δn_i и τ_i строят три линии положення

- Выбирают масштаб построения с учетом рассчитанных величин переносов:

- Через центр бланка, принимаемый за счислимую точку по делениям на рамке проводится направление градиента t₁ первого навигационного параметра.

- Вдоль направления градиента откладывается перенос n₁ по направлению, если перенос положителен, в противоположном – если отрицателен.

- Через полученную точку жирным цветом проводится линия положения, обозначаемая с концов римской цифрой I.

- Для построения второй линии положения производятся действия 1-3.

- Пересечение линий положения даёт фигуру погрешности, которая может отличаться от фогуры погрешности на карте из-за замены изолиний на ЛП .

2.5 Среднеквадратическую погрешность или смещение ЛП рассчитывают по формуле:

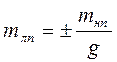, где: m_нп – СКП навигационного параметра,

g – его градиент. В нашем случае:

Для пеленгов: т_лп1=т_П/g _П = СКПП_о/g _П= ; для дистанции т_лп2 ⁼ СКПД_о/g_D =

По значениям смещений ЛП определяют абсолютные веса ЛП Р = 1/( m_нп)² и затем, при необходимости, определяют относительные веса ЛП: Р_i = Р_i/Р_наиб.

С помощью штурманского приема находят вероятнейшее место судна внутри фигуры погрешности. В правой нижней части бланка рассчитывают обсервованные координаты места судна по формулам: j₀=j_с+Dj; l₀=l_с+Dl.

Используя центографический метод сначала рассчитывают веса точек пересечения фигуры погрешности по формулам: 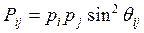. Обратно пропорционально весам точек пересечения находят промежуточные точки сторон фигуры погрешности, приписывая этим точкам сумму весов на концах соответствующей стороны. Соеденяют промежуточную точку с незадействованной на первом шаге точкой пересечения ЛП и аналогично первому этапу определяют вероятнейшее место судна. Сравнивают полученный результат ОМС центрографическим методом с применением штурманского приема.

2.6 На свободном месте карты в крупном масштабе строят полигон весов как векторную сумму трех абсолютных весов под двойными углами каждой ЛП к северной части меридиана (Nи). Снимают с полигона весов в масштабе построения величину разности весов полуосей

Эллипса и направление большой полуоси к Nи. Рассчитывают элементы эквивалентного эллипса погрешностей.

Величина результирующего вектора построения дает величину 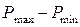в масштабе построения, а его угол с его угол с N_u равен 2b₀.

Арифметическая сумма даст величину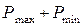

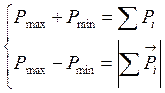
решив систему уравнения полуосей эллипса получим:

,

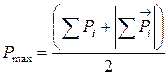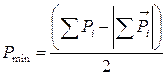
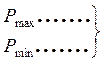веса полуосей эллипса

2.7 Радиальная СКП места судна рассчитывается по е

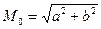
налитически

3.1 При аналитическом методе координаты места судна получают совместным решением системы исходных уравнений ЛП: Для их получения выполняются все действия по пунктам 3.1 – 3.4 как и при графоаналитическом решении.

3.5 Составляется таблица для получения нормальных уравнений по методу наименьших квадратов. В таблицу заносят числовые исходные данные уравнений исходных ЛП:

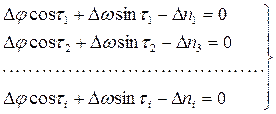
Произведя замены:

a_i=cost_i,

b_i=sint_I,

l=-Dn

заносим исходные данные в расчетную таблицу аналитической обработки исходной информации.

i

τ

a

b

l

P

Paa

Pab

Pal

Pbb

Pbl

Pll

Σ

Σ

Σ

Σ

Σ

Σ

[Paa]

[Pab]

[Pal]

[Pbb]

[Pbl]

[Pll]

3.6 Решив систему методом наименьших квадратов, мы получим систему двух уравнений, называемых нормальными для равноточных измерений:

и для неравноточных.

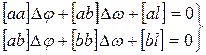
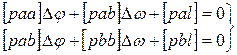
Решив, данную систему методом определителей получим:

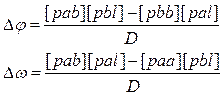
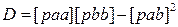
Систему нормальных уравнений можно так же решить методом итераций: в этом случае выделяем неизвестные, после чего система выглядит следующим образом:

( 50 )

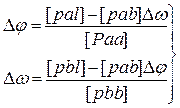
В первом приближении примем Dw = 0:

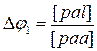, для Dw₁ учтём, уже найденное Dj₁:

.

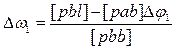Второе приближение:

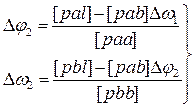
Вычисления продолжают до тех пор, пока разность между двумя последовательными приближениями не окажется в пределах заданной точности e.

Удобство метода - в однообразии расчетов и простоте машинного алгоритма. Полученный таким путем результат ОМС не означает, что обсервованные координаты j₀ и l₀ имеют точность в пределах e, точность j₀ и l₀ оценивается эллипсом или радиальной СКП которых зависит от точности исходных ЛП.

Пример: Расчёт коэффициентов нормальных уравнений.

Дано: Направления градиентов, переносы и СКП 4 линий положения:

№	t	Dn	mлп
5.	191,7°	-0,9′	0,8
6.	56,2°	0,1	1,2
7.	31,7°	1,0	1,0
8.	79,7°	-0,7′	0,5

Рассчитать: коэффициенты нормальных уравнений.

t	a (cost)	b (sint)	l (-Dn)	p	paa	pab	pal	pbb	pbl
191,7°	-0,97	-0,20	0,9′	1,6	1,50	0,31	-1,45	0,06	-0,30
56,2°	0,55	0,83	-0,1	0,7	0,22	0,32	-0,03	0,48	-0,04
31,7°	0,85	0,52	-1,0′	1,0	0,72	0,45	-0,83	0,28	-0,51
79,7°	0,17	0,98	0,7′	4,0	0,13	0,70	0,51	3,87	2,83
				Σ	2,56	1,78	-1,79	4,69	1,98

3.7 Для расчета эллипса используют уравнения исходных ЛП и их решение методом наименьших квадратов. Поскольку оценка точности места судна выполняется после расчета вероятнейшего места судна как центра эллипса с координатами j₀ и l₀, то итоги вычисления нормальных уравнений легко применить для расчета эллипса погрешностей.

Порядок расчетов:

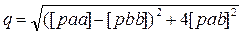
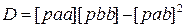
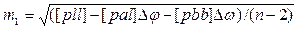
Для n>2

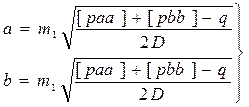
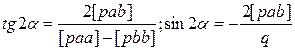
Полуоси можно рассчитать и иным путём:

,

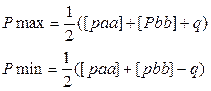
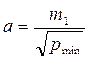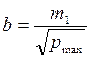
Погрешность по широте и отшествию:

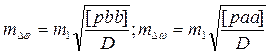
3.8 Проверяют значение радиальной СКП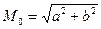

Список рекомендованной литературы

Основная литература:

1. Кожухов В.П. Математические основы судовождения / В.П. Кожухов, В.В. Григорьев, С.М. Лукин - М.: Транспорт, 1987 - 208 с.

2. Груздев Н.М. Оценка точности морского судовождения / Н.М. Груздев - М.: Транспорт, 1989 -192 с.

3. Навигация / Ю.К. Баранов, М.И. Гаврюк, В.А. Логновский, Ю.А. Песков.- Санкт-Петербург 1997 - 510 с.

4. Задачник по навигации и лоции /М.И. Гаврюк В.В. Григорьев, С.М. Лукин - М. Транспорт 1984 - 212 с.

Дополнительная литература:

5. Алексишин В.Г. Обеспечение навигационной безопасности плавания / В.Г. Алексишин, Л.А. Козырь, С.В. Симоненко. – М. Издание «Феникс» 2009. -517 с.

6. Кондрашихин В.Г. Теория ошибок. / В.Г. Кондрашихин - М.: Транспорт 1969. -256 с

7. Управление промысловыми судами. - Калининград:. Кн. изд.1969. – 307 с.

8. . Михайлов В.С. Навигация и лоция / В.С. Михайлов, В.Г. Кудрявцев, О.В. Шмыгалев - К.: Издательство «Компас», 2010. -831 с.

9. Михайлов В.С. Обеспечение навигационной безопасности плавания / В.С. Михайлов, В.Г. Кудрявцев, Д.А. Соколовский – К. Издательство «Компас», 2010. – 566 с.

10. Мореходные таблицы (МТ-2000) – Санкт-Петербург: МО РФ ГУН и О №9011, 2002. 576 с.

11. .. Логиновский В.А. Комплексная обработка навигационных измерений / В.А. Логиновский, С.В. Смоленцев - Одесса: Мортехинформреклама 1988, -322 с.

12. . Рыбалтовский Н.Ю. Математическая обработка задач судовождения / Н.Ю. Рыбалтовский - М.: Морской транспорт 1959. – 182 с.

13. Ющенко А.П. Способ найменьших квадратов / А.П. Ющенко - М.: Морской транспорт 1981. - 206 с.

14. Николаев А.В. Оценка точности плавания судов флота рыбной промышленности / А.В. Николаев. - М.: Пищевая Промышленность, 1977. - 143 с.

15. 15. Кондрашихин В.Т. Определение места судна / В.Т. Кондрашихин - М.: Транспорт 1989. - 231 с.

16. ГОСТ Р 51794-2001. Системы координат. Методы преобразования координат определяемых точек. Дата введения 01.07.2002.

17. Пазынич Г.И. Математические основы судовождения / Г.И. Пазынич. – Керчь, КГМТУ, учебное пособие 2009 - 247 с.

18. Пазынич Г.И. Математические основы судовождения / Г.И. Пазынич. – Керчь, КГМТУ, конспект лекций 2012 - 95 с.

© Георгий Иванович Пазынич

Методические указания по выполнению курсовой работы

курсантами третьего курса очной и заочной формы обучения

специальности 26.05.05 «Судовождение»

Тираж______экз. Подписано к печати______________

Заказ №________ Объем 2,49 п.л.

Изд-во ФГБОУ ВО «Керченский государственный морской технологический университет»

298309 г. Керчь, Орджоникидзе, 82.