М.8.4. Какие напряжения называются главными нормальными и какие главными касательными? Сколько главных напряжений в плоской и сколько в пространственной задачах?

Главные нормальные напряжения - это нормальные напряжения, действующие на площадки, на которых отсутствуют касательные напряжения. Главные касательные напряжения - это максимальные касательные напряжения. Если обозначить главные нормальные напряжения через s 1, s 2 и s 3, то главные касательные напряжения равны соответственно:

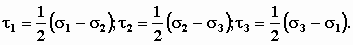
Главных нормальных напряжений в пространственной задаче - три, в плоской - два. Главных касательных напряжений в случае пространственной задачи - три, в случае плоской задачи - одно.

М.8.5. Что такое изолинии напряжений и какой вид имеют изолинии главных напряжений в случае плоской задачи, когда на участке границы полуплоскости приложена равномерно распределенная нагрузка?

Изолинии напряжений - это линии, во всех точках которых соответствующие напряжения равны. Изолинии главных напряжений, как наибольшего, так и наименьшего, представляются дугами окружностей, проходящих через концевые точки загруженного участка.

М.8.6. Какой вид имеют эпюры вертикальных нормальных напряжений s z в случае плоской задачи, когда на участке границы приложена равномерно распределенная нагрузка?

Эпюры вертикальных нормальных напряжений s z изображены на рис. М.8.6.

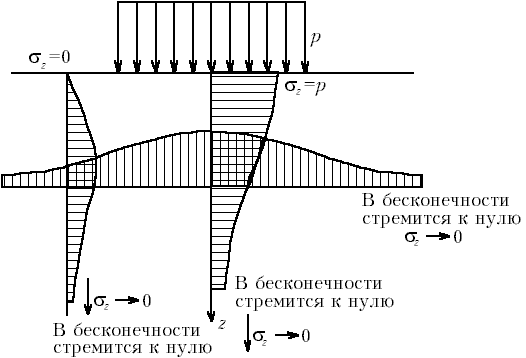Рис.М.8.6. Эпюры напряжений при равномерно распределенной нагрузке на конечном участке полуплоскости или полупространства

М.8.7. Какие безразмерные координаты приняты в нормах (СНиП) для расчета напряжений?

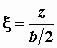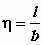Для расчета напряжений в нормах (СНиП) приняты две относительные координаты x и h , причем и , где b - ширина (наименьшая сторона) подошвы прямоугольного фундамента, l - его длина (всегда l³ b).

М.8.8. При каком значении , где l - длина загруженного участка, b - его ширина, считается, что напряжения s z в пространственной и в плоской задачах практически можно считать совпадающими?

Считается, что при h = 10 мы имеем значения напряжений s _z, которыми для практических целей можно пользоваться и в случае плоской деформации, то есть когда следовало бы считать h =¥ .

М.8.9. Каким образом, зная эпюру напряжений s z вдоль оси z при равномерно распределенной нагрузке, действующей на участке шириной b, построить эпюру s z, если нагрузка будет действовать в пределах участка шириной 2b? Как будет трансформироваться эпюра s z при дальнейшем увеличении ширины участка, в пределах которого она приложена?

Если имеется эпюра напряжений s _z при ширине загруженного участка b, то, зная ординату s _z на глубине z, нужно эту же ординату для случая ширины 2b отложить на глубине 2z и т.д. (рис.М.8.9).

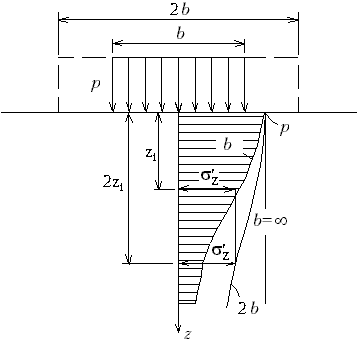Рис.М.8.9. Изменение эпюры s z в случае плоской задачи при увеличении ширины загруженного участка

При дальнейшем росте ширины загруженного участка напряжения будут все медленнее рассеиваться и при увеличении b до бесконечности эпюра s _z будет иметь постоянную ординату s _z =p. Все эти эпюры имеют верхнюю ординату, равную p, и выходят поэтому из одной точки.

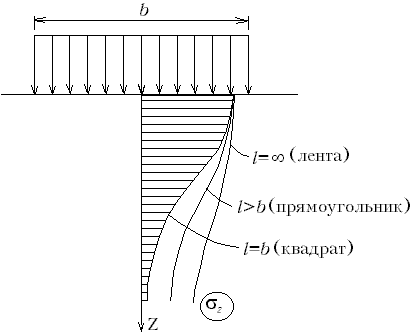Рис.М.8.10. Изменение эпюры s z в случае пространственной задачи при постоянной ширине загруженного участка и изменении его длины

М.8.10. Каким образом будет трансформироваться эпюра вертикальных напряжений s z в случае, если одна и та же равномерно распределенная нагрузка на поверхности приложена в пределах квадрата, прямоугольника, ленты при одной и той же ширине b? Чем больше длина l (наименьшая сторона называется шириной b, поэтому всегда l³ b), тем "полнее" эпюра напряжений s z (рис.М.8.10).