Прогнозирование по Линейной множественной регрессионной модели

Самостоятельная работа № 2

Часть1

ПРОГНОЗИРОВАНИЕ С ПОМОЩЬЮ ПОЛИНОМИАЛЬНОЙ МОДЕЛИ

Цель: По опытным данным построить уравнение регрессии вида .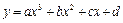

Задание: Рассматривается зависимость урожайности некоторой культуры y_i от количества внесенных в почву минеральных удобрений x_i. Предполагается, что эта зависимость квадратичная. Необходимо найти уравнение регрессии вида .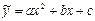

х
у	26,6	45,7	63,8	78,3	86,4	97,7	96,9	113,6	113,6	120,9

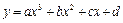. Для нахождения коэффициентов 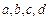нужно решить систему уравнений:

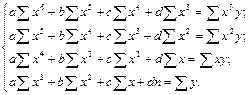
											сумма
х
у	26,6	45,7	63,8	78,3	86,4	97,7	96,9	113,6	113,6	120,9	843,5
х^2
x^3
x^4
x^5
x*y		45,7	127,6	234,9	345,6	488,5	581,4	795,2	908,8	1088,1	4615,8
x^2*y		45,7	255,2	704,7	1382,4	2442,5	3488,4	5566,4	7270,4	9792,9	30948,6
Регрессия	28,32	49,12	68,26	85,74	101,56	115,72	128,22	139,06	148,24	155,76	175940,9

Теперь решаем систему уравнений:

A=
Аобр.=	0,00189	-0,017	0,0227
	-0,017	0,166	-0,259
	0,0227	-0,259	0,618

В=	30948,6
	4615,8
	843,5
Коэффициенты	-0,83
	21,63
	28,32

Получаем

у= -0,83х^2+21,63х+28,32

Регрессия

28,32

49,12

68,26

85,74

101,56

115,72

128,22

139,06

148,24

155,76

175940,9

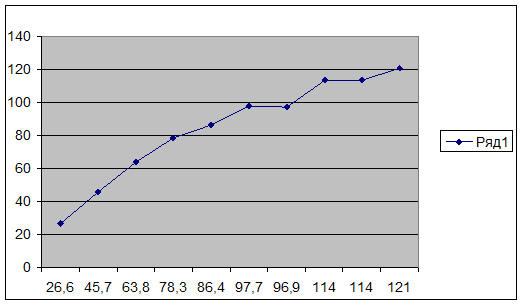
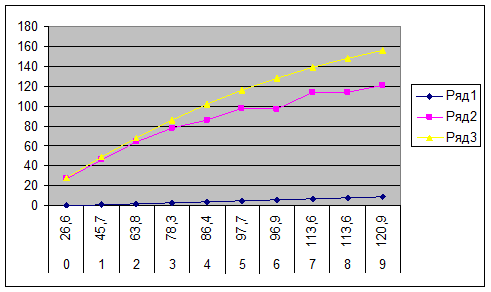
Построим графики исходных данных и полученных на основании уравнения регрессии.

Часть2

Прогнозирование по Линейной множественной регрессионной модели

Задание 1.

Цель: По опытным данным построить уравнение множественной линейной регрессии и определить его характеристики.

Построим линейное уравнение множественной регрессии. Для этого предварительно исследуем матрицу парных коэффициентов корреляции.

Х1
Х2
y	30,8	31,1	30,4	31,7	30,5	33,5		34,5		32,9

Для общей оценки мультиколлинеарности факторов и адекватности регрессионной модели рассчитаем определители матриц 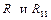. Сформируем полную матрицу парных коэффициентов корреляции.

	Х1	Х2	y
Х1		-0,91743	0,659697
Х2	-0,91743		-0,58054
y	0,659697	-0,58054

R=	0,088806
R11=	0,158314

Найдем теперь коэффициент множественной корреляции.

Rху=

0,662608

Результат 0,662608 говорит о в принципе высокой связи между фактором и функцией отклика.

Проведем теперь отбор факторов.

Факторы можно считать коллинеарными (интеркоррелированными), если их парный коэффициент по модулю больше 0,7. В нашем случае таких пар факторов нет. Все факторы можно считать независимыми друг от друга и использовать в регрессионном уравнении. Определим теперь влияние каждого фактора 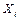на функцию отклика Y. Для этого рассмотрим коэффициенты парной корреляции: Rx1x2=-0,91743, Rx1y=0,659697, Rx2y=0,58054. Видно, что третий коэффициент 0,58054 намного меньше по модулю, чем примерная граница 0,7, поэтому влияние третьего фактора Х₂ на результат мало и его можно отбросить из рассмотрения.

Линейная	0,4167476	29,15607	#Н/Д
	0,1678538	1,332298	#Н/Д
	0,4351998	1,523683	#Н/Д
	6,164302		#Н/Д
	14,311112	18,57289	#Н/Д

Первая строка результата – значения параметров регрессионного уравнения 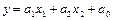- числа 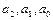. .Следовательно, уравнение регрессии имеет вид у=29,16х1+0,42х2.

Вторая строка – стандартные ошибки коэффициентов. Все они меньше самих коэффициентов, это значит, что коэффициенты значимы. Коэффициент детерминации=0,435, что говорит о наличии не сильной связи. идно, что F-критерий регрессионной модели равен 6,16. Проверим модель на адекватность. Вычислим критическое значение статистики.

F-критическое=

5,317655

Видно, что F-статистика больше ее критического значения, поэтому модель адекватна.

Задание 2.

Отобрать факторы и построить регрессионную модель для данных.

Х1

Х2

Х3

Х4

Y

	Х1	Х2	Х3	Х4	Y
Х1		-0,88994	0,376987	0,968184	-0,9526
Х2	-0,88994		-0,59595	-0,89719	0,878017
Х3	0,376987	-0,59595		0,467119	-0,43245
Х4	0,968184	-0,89719	0,467119		-0,97951
Y	-0,9526	0,878017	-0,43245	-0,97951

R=	0,00022
	0,005563
Rх	0,980008

Х1

Х2

Х3

Y

линейная	-0,10429	0,088831	-1,05268
	0,20954	0,389401	0,284517
	0,914202	1,061996	#Н/Д
	31,96598		#Н/Д
	108,1572	10,15053	#Н/Д

F-критическое

6,991917

Из вышепоказанного видно, F-критическое меньше F-статистика, что говорит об адекватности модели.