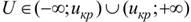Онятие об интервальной оценке параметров распределения.

В ряде задач требуется не только найти для параметра θ подходящее численное значение, но и оценить его точность и надежность. Для определения точности и надежности θ∗ в МС вводят понятие доверительного интервала и доверительной вероятности.
Пусть для параметра θ из опыта получена несмещенная оценка θ∗. Оценим возможную при этом ошибку. Назначим некоторую достаточно большую вероятность 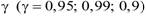такую, что событие с вероятностью γ можно считать практически достоверным. Найдём такое значение ε, ε>0, для которого вероятность отклонения оценки на величину, не превышающую ε, равна γ: 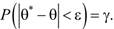(2.20)
Тогда диапазон практически возможных значений ошибки, возникающей при замене θ на θ*, будет равен ± ε. Большие по абсолютной величине ошибки будут появляться с малой вероятностью α =1 −γ .
Перепишем уравнение (2.20) в виде: 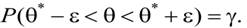(2.21)
Равенство (2.21) означает, что с вероятностью γ неизвестное значение параметра θ попадает в интервал 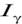, равный 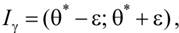(2.22)
который является случайным, т. к. случайным является центр θ* интервала 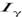.Случайной является и его длина, равная 2ε, т.к. ε, как правило, вычисляется по опытным данным. Поэтому в (2.21)величину γ лучше толковать не как вероятность γ попадания точки θ в интервал 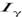, а как вероятность того, что случайный интервал 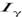накроет точку θ:

θ*– центр доверительного интервала,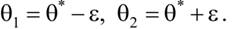

Вероятность γ принято называть доверительной вероятностью (надежностью), а интервал 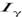– доверительным интервалом.
Интервал 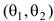будем называть доверительным для оценки параметра, при заданной доверительной вероятности γ или при заданном уровне значимости α = 1− γ, если он с вероятностью γ "накрывает" оцениваемый параметр θ, т.е. 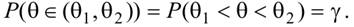(2.23)

Границы интервала 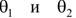называют доверительными границами. Доверительный интервал можно рассматривать как интервал значений параметра θ, совместимых с опытными данными и не противоречащих им. Метод доверительных интервалов был разработан Ю. Нейманом, который использовал идеи Р.Фишера. Рассмотрим вопрос о нахождении доверительных границ 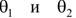. Пусть для параметра θ имеется несмещённая оценка θ*. Если бы был известен закон распределения величины θ*, задача нахождения доверительного интервала была бы весьма простой. Для этого достаточно было бы найти такое значение ε, для которого выполнено соотношение (2.20). Сложность состоит в том, что закон распределения оценки θ* зависит от закона распределения СВξ , следовательно, от его неизвестных параметров, в частности, от параметра θ .

16 Проверка гипотез о среднем значении нормально распределенной СВ при известной дисперсии
Пусть имеется генеральная совокупность X, распределенная по нормальному закону с известной дисперсией 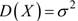(т.е. σ известно). Генеральная средняя a неизвестна, но есть основания предполагать, что она равна предполагаемому значению 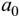. Из нормальной генеральной совокупности X извлечем выборку 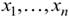объема n, по которой найдем 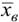. При этом дисперсия 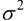известна . Поскольку предполагается, что 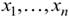как СВ 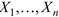взаимно независимы, то они имеют одинаковые нормальные распределения, а следовательно, и одинаковые характеристики ( мат ожидание, дисперсию, и т.д .). Необходимо по известному 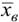при заданном уровне значимости α проверить гипотезу 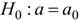о равенстве генеральной средней a гипотетическому значению 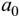. Сформулируем правила проверки гипотезы 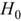обозначив через 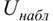значение критерия, вычисленное по данным наблюдений.

Правило 1. Для того чтобы при заданном уровне значимости α проверить гипотезу 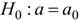о равенстве неизвестной генеральной средней a нормальной совокупности с известной дисперсией 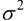гипотетическому значению 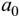при конкурирующей гипотезе 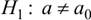, необходимо вычислить 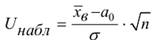(3,5)
и по таблице значений функции Лапласа найти критическую точку двусторонней критической области из равенства 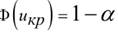(3,6)
Если 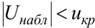– нет оснований отвергнуть гипотезу 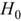; если 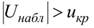– гипотезу 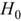отвергают.

Правило 2. При конкурирующей гипотезе 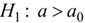критическую точку 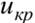правосторонней критической области находят из равенства 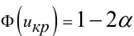(3,7)
Если 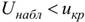– нет оснований отвергнуть гипотезу; если 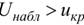– гипотезу 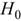отвергают.

Правило 3. При конкурирующей гипотезе 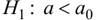критическую точку 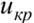находят по правилу 2, а затем полагают границу левосторонней критической области 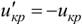. Если 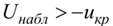– нет оснований отвергнуть гипотезу 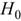; если 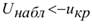– гипотезу 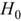отвергают.

Замечание. Из правила 1 следует, что если область принятия гипотезы 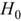есть интервал 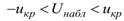, то область ее отклонения –