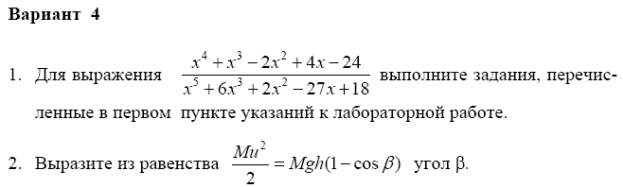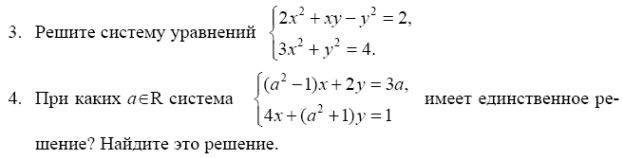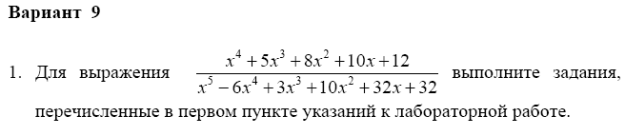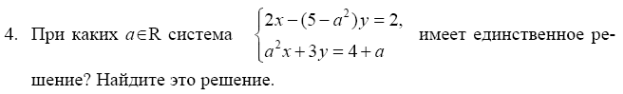Тема Символьные преобразования в MathCAD

Лабораторная работа № 6

6) разложите выражение в ряд Тейлора с точностью до шестого порядка;

7) найдите производную и упростите полученное выражение;

8) найдите интеграл;

9) вычислите определенный интеграл 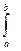от выражения, где 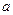- предел выражения при 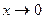, 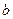- предел выражения при .

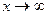Пример решения варианта

Задание 1. Для выражения 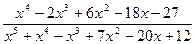выполните задания, перечисленные в первом пункте указаний к лабораторной работе.

Решение.

Задаем в MathCAD выражение:

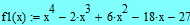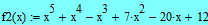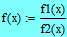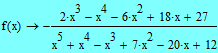1) Находим, все значения x, при которых числитель обращается в 0.

Первый способ (с помощью команд меню Symbolics ► Variable ► Solve (Символика ► Переменная ► Решить)

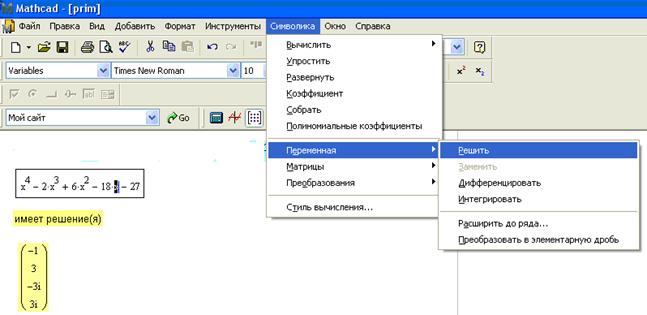
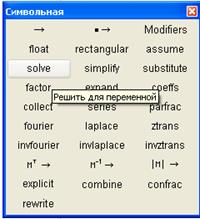
Второй способ (с помощью ключевого слова solve на панели Символьная)

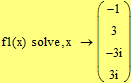Установили, что числитель обращается в 0 в двух действительных точках: 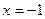и .

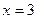2) Выясняем, при каких значениях 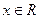выражение не определено. Это будут точки, в которых знаменатель обращается в 0.

Первый способ (с помощью команд меню Symbolics ► Variable ► Solve (Символика ► Переменная ► Решить)

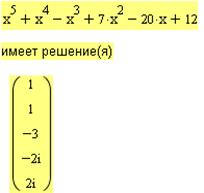
Второй способ (с помощью ключевого слова solve на панели Символьная)

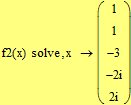Установили, что знаменатель обращается в 0 в двух действительных точках: 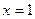и .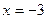

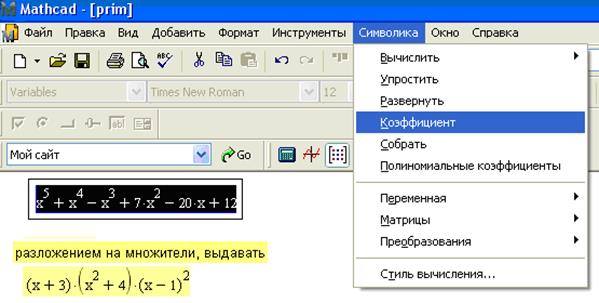
3) Разлагаем знаменатель на множители.

Первый способ (с помощью команд меню Symbolics ► Factor (Символика ► Коэффициент)

Второй способ (с помощью ключевого слова factor на панели Символьная)

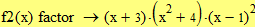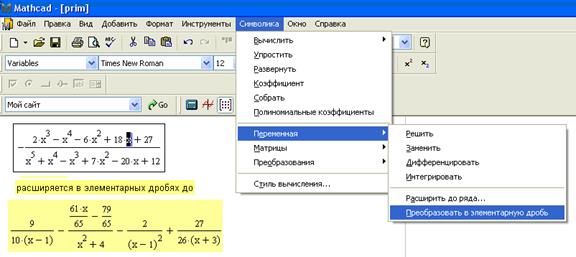
4) Выполняем разложение на элементарные дроби.

Первый способ (с помощью команд меню Symbolics ► Variable ► Convert to Partial Fractions (Символика ► Переменная ► Преобразовать в элементарную дробь)

Второй способ (с помощью ключевого слова parfac на панели Символьная)

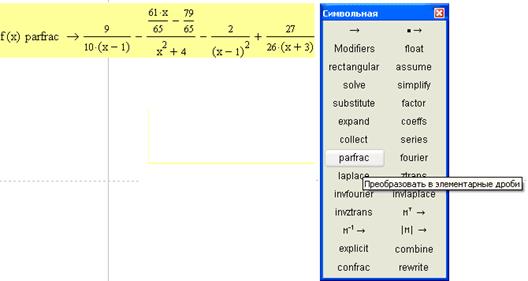
5) Выясним при каких x выражение принимает положительные значения.

Первый способ (с помощью команд меню Symbolics ► Variable ► Solve (Символика ► Переменная ► Решить)

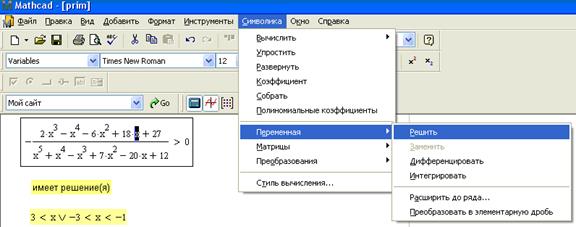
Второй способ (с помощью ключевого слова solve на панели Символьная)

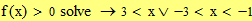Таким образом выражение принимает положительные значения при 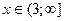либо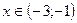

6) Разложим выражение в ряд Тейлора с точностью до шестого порядка:

Первый способ (с помощью команд меню Symbolics ► Variable ► Expand to Series (Символика ► Переменная ► Расширить до ряда)

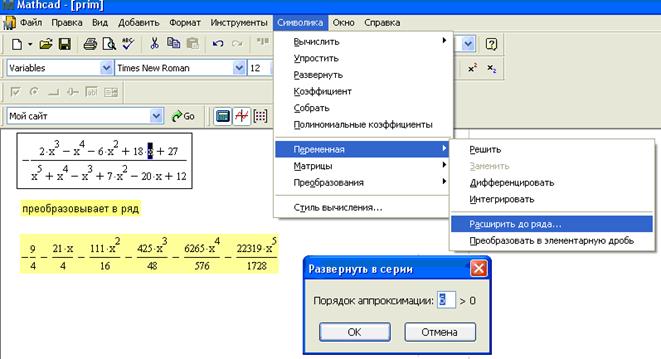
Второй способ (с помощью ключевого слова series на панели Символьная)

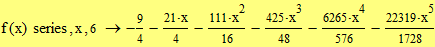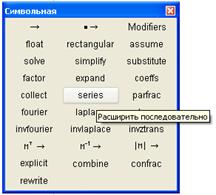
7) Hайдем первую производную:

Первый способ (с помощью команд меню Symbolics ► Variable ► Differentiate (Символика ► Переменная ► Дифференцировать)

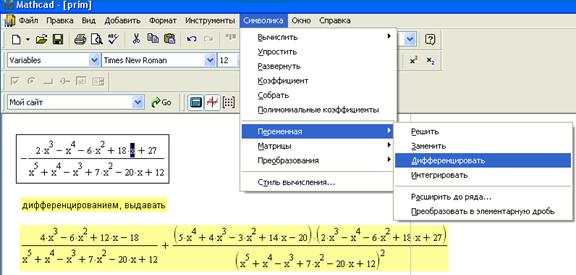
Второй способ (с помощью выбора знака Производная ? на панели Вычисление)

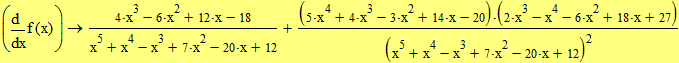Упростим полученное выражение:

Первый способ (с помощью команд меню Symbolics ► Simplify (Символика ► Упростить)

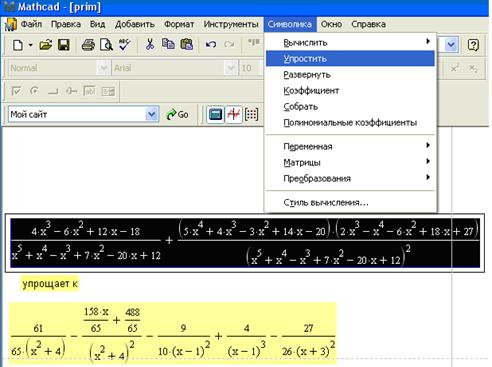
Второй способ (с помощью ключевого слова simplify на панели Символьная)

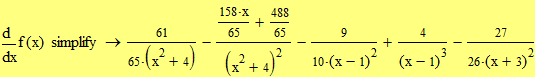
8) Найдем интеграл:

Первый способ (с помощью команд меню Symbolics ► Variable ► Integrate (Символика ► Переменная ► Интегрировать)

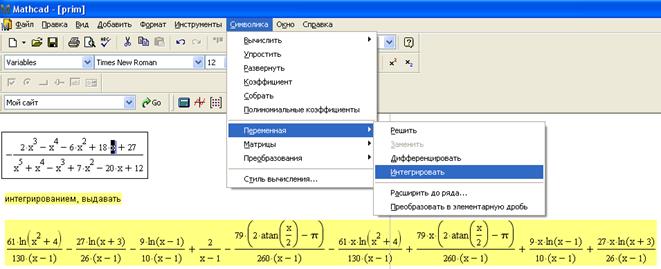
Второй способ (с помощью выбора знака Неопределенный интеграл на панели Вычисление)

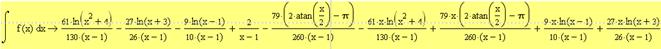
9) Вычисляем определенный интеграл 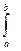от выражения, где 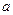- предел выражения при 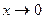, 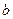- предел выражения при .

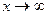Определяем :

Первый способ (с помощью команд меню Symbolics ► Evaluate ► Symbolically (Символика ► Вычислить ► Символически)

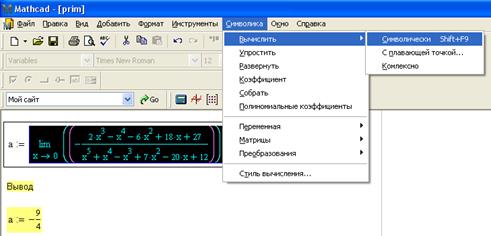
Второй способ (с помощью выбора знака Вычислить символически на панели Вычисление)

Аналогично определяем пределяем :

Первый способ (с помощью команд меню Symbolics ► Evaluate ► Symbolically (Символика ► Вычислить ► Символически)

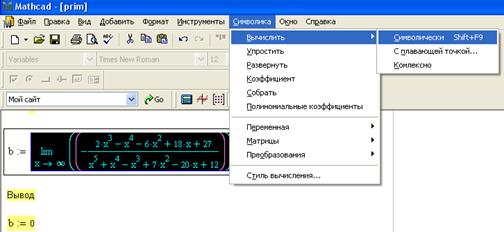
Второй способ (с помощью выбора знака Вычислить символически на панели Вычисление)

Вычисляем определенный интеграл:

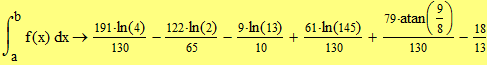Задание 2. Выразите из равенства 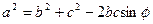угол .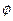

Решение:

Первый способ (с помощью команд меню Symbolics ► Variable ► Solve (Символика ► Переменная ► Решить)

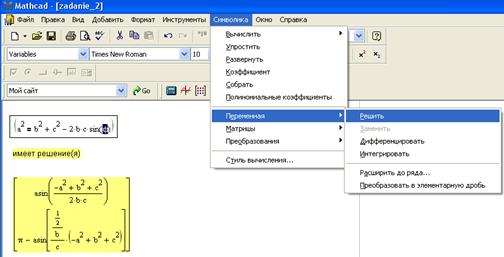
Второй способ (с помощью ключевого слова solve на панели Символьная)

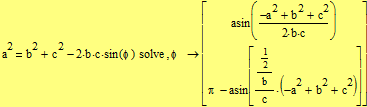Таким образом имеем два решения:

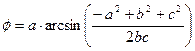и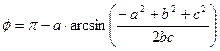

Задание 3. Решите систему уравнений .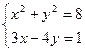

Первый способ (с помощью ключевого слова solve на панели Символьная)

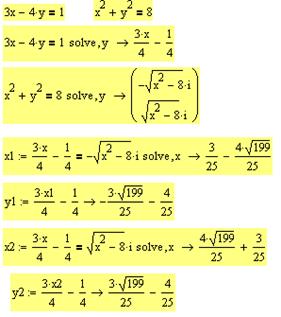
Второй способ (с помощью блока решений Given-Find)

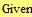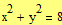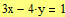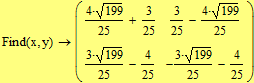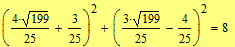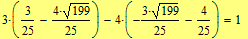Задание 4 При каких 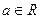система 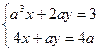имеет единственное решение ? Найдите это решение.

Находим точки 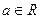при которых определитель равен 0.

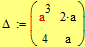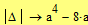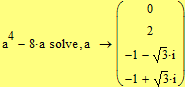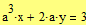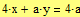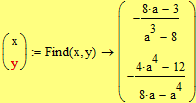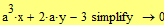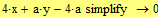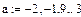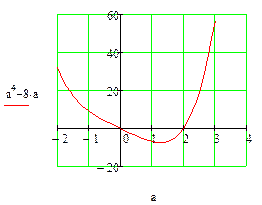Установил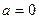и: при и при 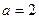система не имеет решений или имеет бесчисленное множество решений.

Ищем решение системы с помощью блока решений Given-Find.

Установили решение системы:

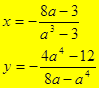
Варианты заданий