Связь между решениями неоднородных и однородных систем.

Пусть дана система линейных неоднородных уравнений.

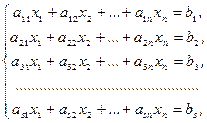(15)

Система линейных однородных уравнений:

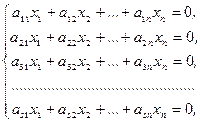(16)

полученная из системы (15) заменой свободных членов нулями, называется приведенной системой для системы (15). Между решениями систем существует тесная связь:

1. Сумма любого решения системы (15) с любым решением системы (16) снова решение системы (15).

2. Разность любых двух решений системы (15) служит решением для приведенной системы (16).

3. Найдя одно решение системы линейных неоднородных уравнений (15) и складывая его с каждым из решений приведенной системы (16), получим все решения системы (15), т.е. ,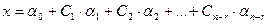

где α₀ – некоторое частное решение системы (15), α₁, α₂, α₁, … , α_n-r – векторы-решения фундаментальной системы решений системы (16), r – ранг матрицы системы (15), - C_i – произвольные постоянные.

☺ Пример 95. Найти обшее решение системы уравнений:

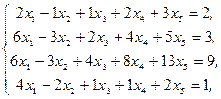
если известно частное решение этой системы: x₁ =1, x₂ =2, x₃ =-1, x₄ =0, x₅ =1.

Решение: Для заданной системы приведенная система уравнений имеет вид:

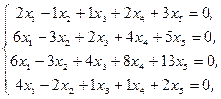
Выполняя стандартные операции по определению ранга матрицы А, получаем: ранг матрицы равен 3. В качестве базового минора удобно использовать минор 3-го порядка:

,

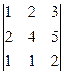включающий первые две и четвертую строки и последние три столбца матрицы. Это значит, что для дальнейшего решения системы можно использовать только первые два и четвертое уравнения, а в качестве свободных неизвестных объявить , x₁ и x₂ .

Перепишем систему уравнений:

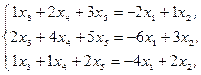
определитель этой системы d = 1. Далее, по правилу Крамера получаем:

, ,

, ,

, ,

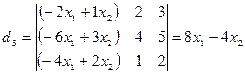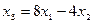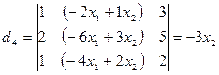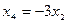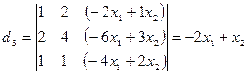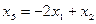Полученные выражения для x₃, x₄ и x₅ представляют общее решение приведенной системы уравнений: принимая произвольные значения для x₁, x₂ и x₃ , будем получать бесчисленное количество частных решений этой системы.

Одно из частных решений получим, задавая значения x₁, x₂ и x₃ , выбирая строки определителя порядка (n-r):

,

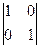где n – число неизвестных системы, r – ранг матрицы А системы.

Максимальная система независимых векторов-решений, т.е. фундаментальная система решений приведенной системы имеет вид:

Обозначение решения	x1	x2	x3	x4	x5
α1 =					-2
α2 =			-4	-3

Используя фундаментальную систему решений, общее решения рассматриваемой системы однородных уравнений можно (т.е. выражение для произвольного решения) записами в виде:

,

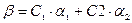где С₁ и С₂ – произвольные постоянные.

Используя частное решение заданной системы и фундаментальную систему решений при-веденной системы уравнений, общее решение исходной системы уравнений можно записать в виде:

.

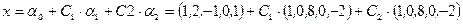Ответ: Общее решение: ;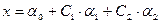

частное решение: α₀ = (x₁ =1, x₂ =2, x₃ =-1, x₄ =0, x₅ =1),

☻Решите примеры:

Пример 96. Найти обшее решение системы уравнений:

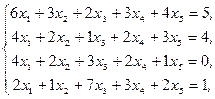
если известно частное решение этой системы: x₁ =1, x₂ =1, x₃ =2, x₄ =-8, x₅ =4.

Ответ: частное решение: x₁ =1, x₂ =1, x₃ =2, x₄ =-8, x₅ =4.

. общее решение: ,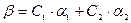

где:

Обозначение решения	x1	x2	x3	x4	x5
α1 =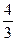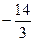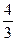
α2 =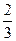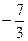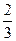

Вопросы для самопроверки:

1. Является ли линейным векторным простронством множество всех решений однородной системы линейных уравнений с обычными операциями сложения и умножения на число?

2. Какова размерность линейного пространства решений однородной системы 8 линейных уравнений с 12 неизвестными, если ранг матрицы системы равен 4?

3. Что называется фундаментальной системой решений (ФСР) однородной системы линейных уравнений?

4. Как построить ФСР однородной системы линейных уравнений?

5. Сколько ФСР можно построить для заданной однородной системы линейных уравнений?