Методика расчета погрешностей косвенных измерений

Большинство измерений в лабораторном практикуме по физике являются косвенными. Ошибка результата косвенного измерения зависит от ошибок всех прямых измерений, а также от вида той математической формулы, которая связывает искомую с непосредственно измеряемыми величинами. Пусть искомая физическая величина γ связана с непосредственно измеряемыми величинами А, В, С, … какой-то функциональной зависимостью:

,

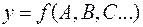искомое значение ХХХ находят путем подстановки в формулу (1.3) средних значений А, В, С, т.е. 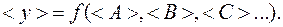Если искомая величина у является функцией многих переменных, то сначала удобно найти относительную погрешность результата, а затем, используя соотношение 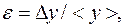найти абсолютную погрешность 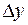. Рассмотрим, как находят выражение для расчета относительной погрешности косвенного результата. Воспользуемся для этого законами дифференциального исчисления, считая непосредственно измеряемые величины А, В, С,… аргументами, а косвенно измеряемую величину у – функцией этих переменных.

Искомую функцию (расчетную формулу) логарифмируют:

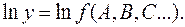
Находят полный дифференциал логарифма функции:

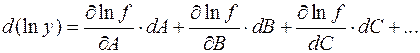(1.6)

Здесь 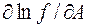– частная производная от ln f (А, В, С…) по аргументу А и т.д. Частная производная находится обычным дифференцированием функции по аргументу А в предположении, что все другие аргументы В, С,…, кроме А, – константы.

Заменяют в полученном выражении (1.6) знак дифференциала d знаком абсолютной погрешности .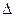

Каждое слагаемое выражения (1.6) возводят в квадрат и получают следующую формулу для расчета относительной ошибки косвенного результата:

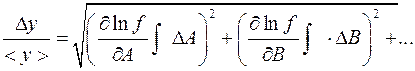
. (1.7)

Подставляют значения абсолютных ошибок прямых измерений 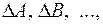средние значения < A >,< B > и рассчитывают относительную ошибку ε, а затем – абсолютную .

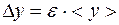Сравнивают слагаемые в выражении (1.7), чтобы выяснить влияние ошибок различных аргументов (А, В,…) на окончательный результат. Делают заключение, какие физические величины необходимо измерить с большей точностью.

Лабораторная работа 1. ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ
РАЗМЕРОВ ТЕЛА (4 ч)

Цель – овладеть техникой физических измерений линейных размеров тел, освоить методику подбора и использования измерительных приборов в прямых измерениях.

Приборы и материалы: штангенциркуль, микрометр, исследуемое тело.

Теория линейного нониуса

Линейные размеры тела можно определить с точностью до 1 мм обычной масштабной линейкой. Для измерения с точностью до долей миллиметра применяется нониус – устройство, позволяющее повысить точность многих измерительных приборов.

Линейный нониус представляет собой небольшую линейку N, скользящую вдоль обычной линейки.

Пусть на нониусе m делений (рис. 1.1), которые наносят так, чтобы длина всех делений нониуса была равна длине (m – 1) наименьших делений масштабной линейки. Пусть b – длина деления масштабной линейки, а – цена деления нониуса. Тогда m ∙ a определяет длину всех делений нониуса, а (m – 1) ∙ в – длину делений масштабной линейки. Очевидно,

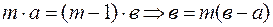или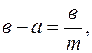

где 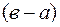– точность нониуса.

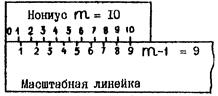
Рис. 1.1

Пример. Цена наименьшего деления шкалы масштабной линейки в = 1 мм, на нониусе m = 20 делений.

Точность нониуса:

.

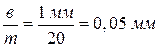Измерения с помощью линейного нониуса производят следующим образом: совмещают левый конец измеряемого тела с нулевым делением масштабной линейки, а к правому концу подводят нониус (рис. 1.2).

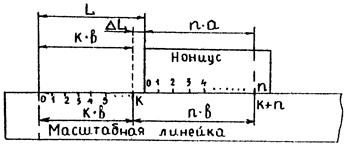
Рис. 1.2

Если правый конец тела оказался между К и К + 1 делениями масштабной линейки, то длина измеряемого тела L равна:

L = K · b +ΔL,

где ΔL – неизвестная пока еще доля (К + 1) деления масштабной линейки.

Обозначим через n деление нониуса, которое совпадает с каким-то делением масштабной линейки. Из рис. 1.2 видно, что номер этого деления К + n. Тогда

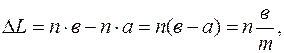
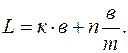
Следовательно, чтобы найти длину измеряемого тела с помощью нониуса, необходимо определить число целых наименьших делений масштабной линейки, укладывающихся по длине тела, и записать их длину, к ней прибавить неизвестную длину ΔL, определяемую произведением точности нониуса на номер деления нониуса, совпадающего с одним из делений масштабной линейки ( ).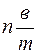

Штангенциркуль состоит из шкалы прибора Д в миллиметровом масштабе, жестко связанной со щекой А (рис. 1.3).

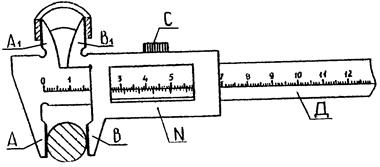
Рис. 1.3

Вдоль шкалы масштаба может перемещаться нониус N, с которым жестко связана вторая щека В. Подвижная часть штангенциркуля снабжена зажимным винтом С. Когда между щеками А и В отсутствует зазор, нулевые метки нониуса и шкалы совпадают. Для промера наружных размеров измеряемый предмет вводят между щеками А и В, которые сдвигают до соприкосновения с предметом. Затем закрепляют подвижную щеку В зажимом С и производят отсчет. Число целых миллиметров отсчитывается непосредственно по шкале прибора до нулевой метки нониуса, число долей миллиметра – по нониусу. При внутренних промерах используют щеки А₁ и В₁. Штангенциркули изготовляют с нониусами, имеющими число делений, равное 10, 20, 50, 100.

Микрометр обычно представляет собой массивную металлическую скобу, на концах которой находятся друг против друга неподвижный упор А и микрометрический винт В, жестко связанный с барабаном С. Барабан делится на 100 или 50 делений. Поступательное перемещение винта измеряется по смещению среза барабана винта вдоль шкалы Д; шаг винта обычно равен 1 или 0,5 мм. Измеряемое тело зажимают между упорами А и В и производят отсчет его размера (рис. 1.4).

Для равномерного нажима микрометрического винта на поверхность измеряемых тел микрометр снабжается фрикционной головкой Е (трещоткой), вращение которой вызывает перемещение винта только до упора его в поверхность измеряемого тела с определенным нажимом, после чего фрикционная головка свободно прокручивается, издавая треск. Шкала имеет верхний и нижний пределы измерений. По нижней шкале необходимо отсчитывать целые миллиметры, по верхней – полумиллиметры, по круговому нониусу барабана – сотые доли миллиметра.

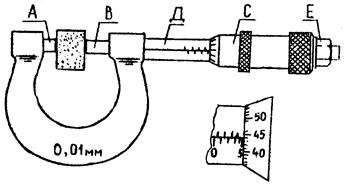
Рис. 1.4

Перед началом измерений микрометром необходимо:

а) определить число делений на барабане и шаг винта;

б) проверить нулевую точку.

Если при соприкосновении упоров А и В против нулевого деления шкалы Д стоит не нулевое деление барабана С, то систематическую ошибку прибора нужно учесть.

Задание 1. Предварительная оценка точности измерения

1. Определить линейные размеры тел с помощью различных измерительных приборов: линейки, штангенциркуля, микрометра.

2. Рассчитать относительные ошибки каждого прямого измерения. В качестве абсолютных погрешностей результатов прямых измерений следует взять приборные ошибки.

3. Сравнить относительные погрешности всех прямых измерений и выделить наименее точно измеренную величину. Для ее определения следует выбрать из имеющегося набора измерительных приборов наиболее точный. Приборы для определения остальных величин подбирают так, чтобы их относительная ошибка была на порядок меньше относительной ошибки наименее точно измеренной величины или того же порядка. Результаты предварительной оценки точности измерения представить в виде табл. 1.2 и сделать заключение.

Таблица 1.2