Закон больших чисел и центральная предельная теорема

Предметом теории вероятностей, как уже отмечалось во введении, являются закономерности, свойственные массовым случайным событиям. Пусть, например, проводится большая серия однотипных опытов. Результат каждого опыта в отдельности случаен и непредсказуем, Так средний результат подчиняется закономерностям и предсказуем. Так, относительная частота появления события в большом числе однотипных опытов является устойчивой величиной и приближается с ростом числа опытов к вероятности данного события. Этот факт лежит в основе всех приложений теории вероятностей к практике. Строгое обоснование приближения средних характеристик большого числа опытов к некоторым постоянным дается утверждениями, которые носят название закона больших чисел.

ЛЕММА. Пусть Х - случайная величина, которая может принимать только неотрицательные значения, т.е. Р(Х<0)=0 и М[Х]=m, тогда P(Х≥1)≤m.

НЕРАВЕНСТВО ЧЕБЫШЕВА. Пусть Х - случайная величина с математическим ожиданием М[Х] = m и дисперсией D[Х] = σ2. Тогда для любого ε > 0, имеет место неравенство

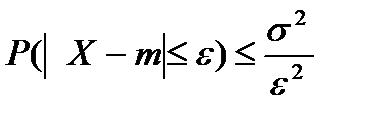
СЛЕДСТВИЕ 1. Используя понятие противоположного события можно переписать неравенство Чебышева в другой форме

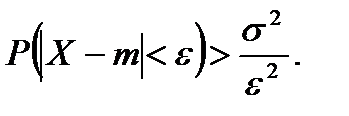
СЛЕДСТВИЕ 2. Правило «трех сигм» для произвольного распределения. Положим ε=3σ, тогда получим

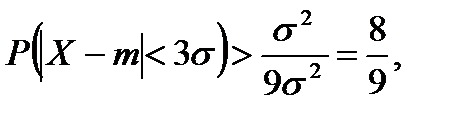
т.е. в интервал ]m-3σ,m+3σ[ для любого распределения попадают не менее 89% всех возможных значений (и наблюдений).

Рассмотрим теперь две теоремы, представляющие собой различные формы закона больших чисел.

ТЕОРЕМА ЧЕБЫШЕВА. Пусть Х1, Х2,...,Хn,... бесконечная после­довательность независимых случайных величин, таких, что их мате­матические ожидания равны

М[Х1]=М[Х2]=...=М[Хn]...=m,

а дисперсии ограничены одним и тем же числом с, т.е.

D[Х1]≤с,D[Х2] ≤с,...,D[Xn] ≤с,...

Тогда, каково бы ни было положительное число ε, вероятность случайного события

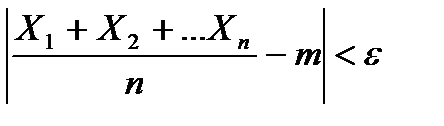
стремится к единице при n→∞.

ЗАМЕЧАНИЕ 1. Мы использовали здесь известную теорему о том, что если для двух последовательностей {аn}и{bn} выполняете аn < bn и их пределы существуют, то

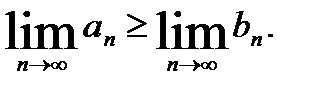
ЗАМЕЧАНИЕ 2. В более конструктивной форме теорему Чебышева можно оставить в виде доказанного неравенства

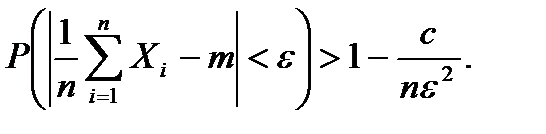
ЗАМЕЧАНИЕ 3. Если дисперсии всех случайных величин равны σ2, то получим

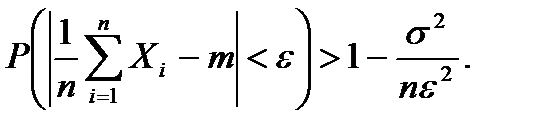
Вероятностный смысл доказанной теоремы заключается в том, что при большом числе n случайных величин их среднее арифметическое практически достоверно» попадает в любую малую ε-окрестность математического ожидания (заштрихованная часть на рисунке).

В указанном смысле среднее арифметическое стремится к математическому ожиданию. Это называется пределом по вероятности и обозначается

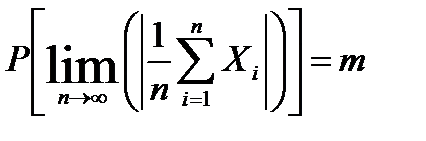
ТЕОРЕМА БЕРНУЛЛИ. Пусть Х - число "успехов" в схеме Бернулли с испытаниями, р - вероятность “успеха” в одном испытании. Тогда каково бы ни было положительное число ε, вероятность события 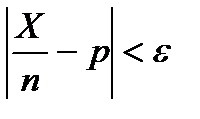стремится к единице при n→∞.

ЗАМЕЧАНИЕ 1. Учитывая замечания 2 и 3 к теореме Чебышева, мы можем теорему Бернулли более конструктивно записать в виде неравенства

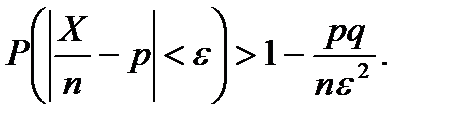
ЗАМЕЧАНИЕ 2 Величина pq=p(1-q) достигает максимума 0.25 при р=q =0.5, поэтому для любой схемы Бернулли

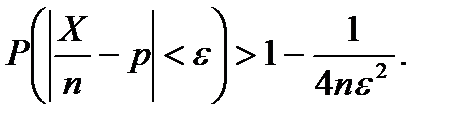
Вероятностный смысл доказанной теоремы заключается в том, что предел по вероятности относительной частоты Х/n в схеме Бернулли стремится к теоретической вероятности «успеха» р в одном опыте. Это подводит строгую теоретическую базу для использования статистического подхода при исчислении вероятностей. Он используется в тех случаях, когда неприменима схема случаев, т.е. нам неизвестна симметрия задачи.

ПРИМЕР 1. Гнутая монета подбрасывается 100 раз. Герб выпал 70 раз. Оценим вероятность выпадения герба для этой монеты. Возьмем ε= 0.1. Тогда получим

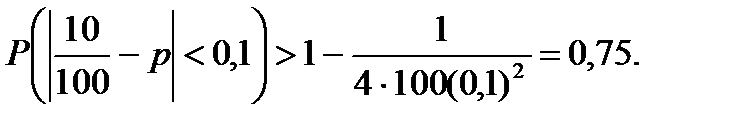
т.е. с вероятностью 0.75 оцениваемое значение р принадлежит интервалу |0.7-p|<0.1 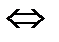0.6<p<0.8.

Аналогично для ε= 0.2 мы получаем, что 0.5 < р<0.9 с вероятностью не менее 0.9375.

В качестве оценки р берем относительную частоту 70/100=0.7.

При увеличении числа испытаний n мы будем получать с вероятностью, близкой к единице, все более маленькие интервалы для оценки теоретической вероятности р.