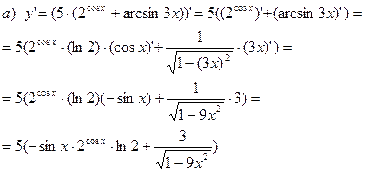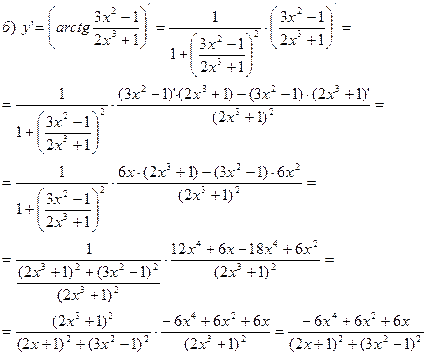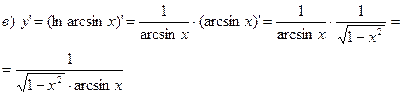Дифференцирование сложной функции

Дифференциальное исчисление функции одной переменной

Производная функции, её геометрический смысл

Пусть функция y = f(x) определена на некотором промежутке. Производной функции y = f(x) по аргументу х называется предел отношения приращения функции Δy к приращению аргумента Δх, когда последнее стремится к нулю:

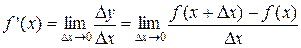
Обозначения: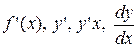

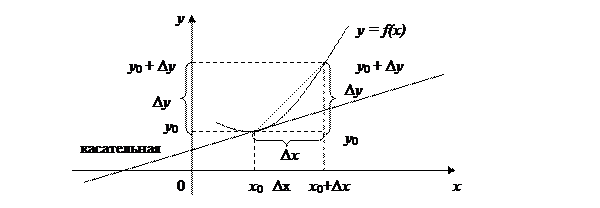
Геометрический смысл производной

Угловой коэффициент касательной к графику функции y = f(x) в данной точке x = x₀ (то есть тангенс угла наклона её к оси ОХ) равен значению производной f’(x) при данном значении аргумента x = x_0.

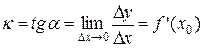
Уравнение касательной к графику в точке с координатами x = x₀ , y = y₀ и с угловым коэффициентом κ.

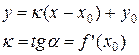
Таким образом

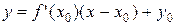
- уравнение касательной к графику функции y = f(x) в точке x = x_0.

Понятие функции, дифференцируемой в точке

Связь между дифференцируемостью и непрерывностью функции

Если функция y = f(x) имеет производную в точке x = x₀, то функция дифференцируема в этой точке.

Теорема. Если функция y = f(x) дифференцируема в данной точке x = x₀, то она в этой точке непрерывна. Обратное неверно.

Дифференциал функции, его геометрический смысл

Дифференциалом dy функции y = f(x) в точке х₀ называется главная, линейная относительно Δх, часть приращения функции в этой точке:

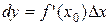
Дифференциалом dx независимой переменной х является приращение Δх этой переменной

dx = Δx

С учетом соотношения

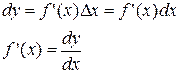
Основные правила и формулы нахождения производных

1. Производная постоянной равна нулю, то есть, если

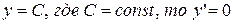
2. Постоянный множитель можно выносить за знак производной, то есть, если

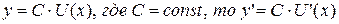
3. Производная суммы конечного числа дифференцируемых функций равна сумме производных этих функций, то есть, если

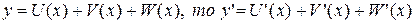
Производная разности конечного числа дифференцируемых функций равна разности производных этих функций, то есть, если

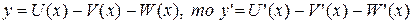
4. Производная от произведения двух дифференцируемых функций равна произведению производной первой функции на вторую функцию плюс произведение первой функции на производную от второй функции, то есть, если

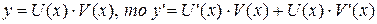
5. Производная дроби (то есть частного от деления двух функций) равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя, то есть, если

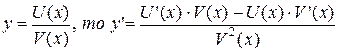
Таблица производных элементарных функций

Функция y	Производная
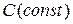х
xn
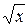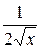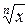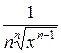ex	ex
ax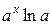

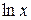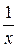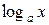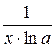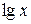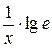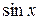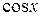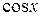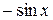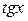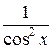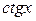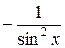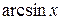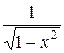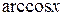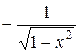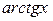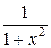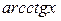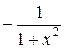Пример. Найти производные следующих функций:

а) ,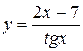

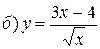
Решение. а)

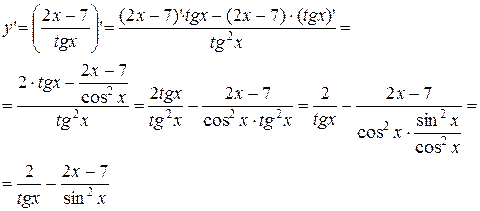
б)

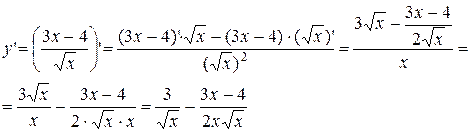
Дифференцирование сложной функции

Пусть 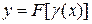- сложная функция, или функция от функции:

,

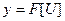где U = .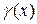

Переменную «U» называют промежуточным аргументом.

Правило дифференцирования сложной функции

Производная сложной функции 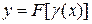по «x» равна произведению производной данной функции по промежуточному аргументу «U» на производную промежуточного аргумента по х:

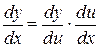или

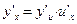
Пример. Найти производные следующих функций:

, ,

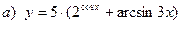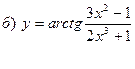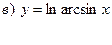
Решение.