Моделирование типовых регуляторов систем электропривода

Цель работы: знакомство с настройками типовых регуляторов систем электропривода и автоматики

На рисунке 7.1 в общем виде представлена структурная схема замкнутой системы автоматического управления.

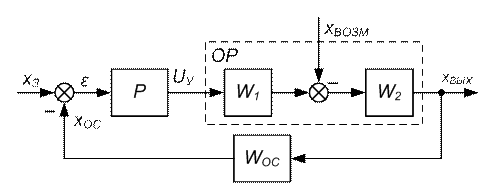Рисунок 7.1 – Структурная схема замкнутой САУ

Замкнутая система автоматического управления (САУ) состоит из объекта регулирования (ОР), датчика(ов) обратной связи (ДОС) с передаточной функцией W_ОС и регулятора (Р). На вход системы поступает сигнал задания x_З, а по каналу обратной связи – сигнал обратной связи x_ОС. На выходе системы в соответствии с сигналом задания и настройкой регулятора формируется выходной сигнал x_ВЫХ.

Объекты регулирования замкнутых САУ можно разделить на статические и астатические, обладающие интегрирующими свойствами. В состав статического ОР входят элементы (устройства), которые могут быть описаны усилительными или апериодическими звеньями. Передаточная функция в разомкнутом состоянии такой системы имеет вид:

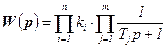, (7.1)

где k_i – коэффициенты усиления элементов системы;

T_i – постоянные времени элементов системы, представленных апериодическими звеньями.

В состав астатического ОР входят элементы, которые представляются усилительными, апериодическими и интегрирующими звеньями. Передаточная функция такой системы имеет вид:

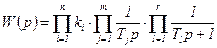, (7.2)

где k_i – коэффициенты усиления звеньев, входящих в состав системы;

T_i – постоянные времени элементов системы, представленных апериодическими звеньями;

T_j – постоянные времени элементов системы, представленных интегрирующими звеньями;

Регулятор – это устройство, которое на основании сигнала ошибки ε вырабатывает управляющее воздействие U_У на объект регулирования такое, чтобы уменьшить ошибку регулирования. Упрощенно структурная схема регулятора представлена на рисунке 7.2.

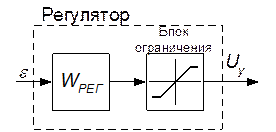Рисунок 7.2 – Структурная схема непрерывного регулятора с насыщением

Непрерывные регуляторы, используемые в САУ электроприводами, следующие пропорциональный (П – регулятор), интегральный (И – регулятор), пропорционально-интегральный (ПИ – регулятор) и пропорционально-интегрально-дифференциальный (ПИД – регулятор) регуляторы.

Применение П – регулятора в замкнутой САУ со статическим ОР позволяет получить статическую по задающему воздействию систему, а в случае с астатическим ОР астатическую по задающему воздействию систему.

Применение И или ПИ – регулятора в системе со статическим ОР позволяет получить астатическую по задающему и возмущающему воздействию (если возмущение одно и неизменно во времени) замкнутую САУ.

В системе с астатическим ОР и применении И или ПИ – регулятора замкнутая САУ будет астатической по заданию и по возмущению, если учитывается только главное (момент сопротивления на валу двигателя) возмущающее воздействие. Однако, САУ с ПИ – регулятором будет обладать большим быстродействием.

Расчет передаточной функции регулятора

Выбор типа регулятора и его настройка (синтез передаточной функции) осуществляется на основании анализа динамических свойств САУ. При использовании принципа последовательной коррекции для синтеза регулятора широко применяются типовые настройки контуров регулирования.

Настройка П – регулятора для системы со статическим или астатическим ОР, как правило, выполняется на основании заданной точности регулирования или быстродействия системы, при условии обеспечения условия устойчивости замкнутой САУ и требуемой величины динамической ошибки.

Расчет передаточной функции регулятора с применением типовых настроек контуров регулирования выполняется в следующем порядке.

1. Задаться желаемой (типовой) передаточной функцией САУ в разомкнутом состоянии. Для систем электропривода применяют настройку контура регулирования на модульный (технический) оптимум или симметричный оптимум (с двукратным интегрированием).

Желаемая передаточная функция разомкнутого контура при настройке на технический оптимум имеет вид:

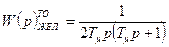, (7.3)

а при настройке на симметричный оптимум вид:

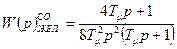, (7.4)

где T_m – малая некомпенсированная постоянная времени;

2. Определить передаточную функцию системы в разомкнутом состоянии:

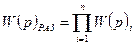, (7.5)

где W(p)_i – передаточные функции звеньев, входящих в замкнутый контур регулирования.

3. Вычислить передаточную функцию регулятора по формуле:

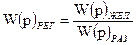. (7.6)

Передаточную функцию регулятора, рассчитанную по формуле (7.6) используют при настройке САУ.

Ход работы

1. Исследование оптимальных настроек системы со статическим ОР. Структурная схема замкнутой САУ со статическим объектом представлена на рисунке 7.3.

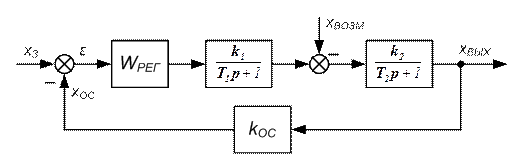Рисунок 7.3 – Структурная схема замкнутой САУ со статическим ОР

1.1 Настройка САУ с использованием П – регулятора

Если для замкнутой САУ, в соответствии с техническим заданием, допустима ошибка регулирования по управляющему воздействию, то её настройка выполняется с использованием П – регулятора. Структурная схема САУ по сигналу ошибки представлена на рисунке 7.4.

Передаточная функция замкнутой САУ по сигналу ошибки от задающего воздействия (x_ВОЗМ(p) = 0) определится выражением:

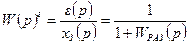, (7.7)

где W(p)^e_ЗАМ – передаточная функция замкнутой САУ по сигналу ошибки;

W(p)_РАЗ – передаточная функция САУ в разомкнутом состоянии;

x_З(p) – операторное изображение сигнала задания;

e(p) – операторное изображение сигнала ошибки.

Рисунок 7.4 – Структурная схема замкнутой САУ по сигналу ошибки

В установившемся режиме ошибка системы по заданию будет равна:

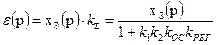, (7.8)

где k_S – суммарный коэффициент передачи САУ;

k₁, k₂ – коэффициенты передачи звеньев САУ;

k_ОС – коэффициента обратной связи;

k_РЕГ – коэффициент передачи регулятора.

Если x_З(p) = 1, то величина ошибки регулирования по задающему воздействию составит:

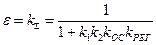. (7.9)

Следовательно, для обеспечения заданной величины статической ошибки регулирования коэффициент усиления П – регулятора должен быть равен:

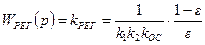. (7.10)

Значение выходного сигнала при этом составит:

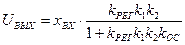или 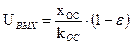, (7.11)

где x_ВХ = x_ОС = 1 – величина входного сигнала и сигнала обратной связи.

Если в системе помимо управляющего имеется возмущающее воздействие, то суммарная ошибка системы e_S будет складываться из ошибки от задающего и от возмущающего воздействия: e_S = e + e_f.

Структурная схема САУ по сигналу ошибки от возмущающего воздействия представлена на рисунке 7.5.

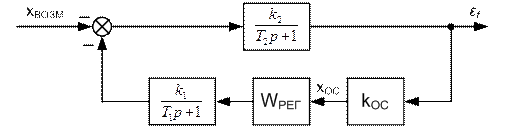Рисунок 7.5 – Структурная схема замкнутой САУ по сигналу ошибки

Передаточная функция замкнутой САУ по сигналу ошибки от возмущающего воздействия (x_З(p) = 0) определится выражением:

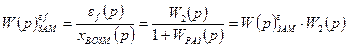, (7.12)

где W(p)^{e f}_ЗАМ – передаточная функция замкнутой САУ по сигналу ошибки, обусловленной возмущением;

W(p)_РАЗ – передаточная функция САУ в разомкнутом состоянии;

x_ВОЗМ(p) – операторное изображение возмущения;

e_f(p) – операторное изображение сигнала ошибки, обусловленной возмущением.

Тогда в установившемся режиме ошибка системы по возмущению будет равна:

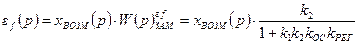, (7.13)

где x_ВОЗМ (p) = 1 – величина возмущающего воздействия.

Уровень ограничения сигнала управления на выходе регулятора рассчитать согласно выражению:

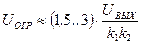. (7.14)

1.2. Настройка САУ с использованием ПИ – регулятора

Если динамика САУ (рисунок 7.3) характеризуется несколькими постоянными времени одна из которых наибольшая 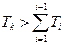, то для повышения быстродействия САУ эта постоянная времени должна быть скомпенсирована. Для этого проводится настройка системы на технический оптимум с использованием ПИ – регулятора.

Передаточная функция системы (рисунок 7.3) в разомкнутом состоянии будет иметь следующий вид:

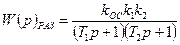, (7.15)

где T₁, T₂ – постоянные времени звеньев САУ;

Тогда, исходя из выражения (7.6), передаточная функция регулятора определиться выражением:

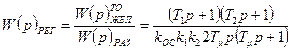. (7.16)

Пускай T₁ минимальная из постоянных времени, то принимая T₁ = T_m , получается передаточная функция ПИ–регулятора:

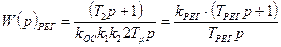, (7.17)

где 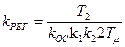– коэффициент передачи ПИ – регулятора;

T_РЕГ = T₂ – постоянная времени ПИ – регулятора.

Уровень ограничения сигнала управления на выходе регулятора рассчитывается согласно выражению (7.14)

Настроенная таким образом САУ является астатической.

1.2. Настройка САУ с использованием И – регулятора

В случае если динамика САУ характеризуется несколькими постоянными времени, имеющими один порядок малости 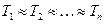, то проводится настройка системы на технический оптимум с использованием И – регулятора.

Передаточная функция системы в разомкнутом состоянии будет иметь следующий вид:

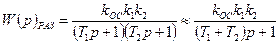. (7.18)

Передаточная функция регулятора по (7.6) определиться следующим образом:

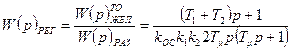. (7.19)

Считая, что сумма постоянных времени 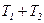достаточно мала, и принимая 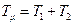, получается передаточная функция И – регулятора:

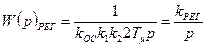, (7.20)

где 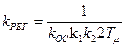– коэффициент передачи И – регулятора.

Уровень ограничения сигнала управления на выходе регулятора рассчитывается согласно выражению (7.14).

Настроенная таким образом САУ является астатической, однако быстродействие системы будет ниже, чем при применении ПИ – регулятора.

1.3. Провести моделирование системы управления в пакете System View с П, ПИ и И – регулятором. Рассчитать переходную характеристику x_ВЫХ(t) при подаче на вход системы единичного ступенчатого воздействия x_З(t) = 1(t) и возмущающего воздействия x_ВОЗМ(t) = 1(t).

1.4. Проанализировать полученные переходные процессы и определить показатели качества регулирования: статическую ошибку регулирования d, перерегулирование s, время регулирования t_Р, время переходного процесса t_ПП и колебательность M.

2. Исследование оптимальных настроек системы управления с астатическим ОР. Структурная схема замкнутой САУ представлена на рисунке 7.6.

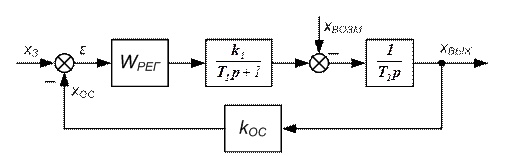Рисунок 7.6 – Структурная схема замкнутой САУ с астатическим объектом регулирования

2.1. Настройка САУ с использованием П – регулятора

Если динамика САУ (рисунок 7.5) характеризуется постоянной времени Т₁ и интегральной постоянной времени Т₂, то система обладает астатизмом первого порядка и является астатической по отношению к задающему воздействию. Если постоянная времени Т₁ не велика и может быть отнесена к малой, то проводится настройка системы на технический оптимум с использованием П – регулятора.

Передаточная функция САУ в разомкнутом состоянии будет иметь следующий вид:

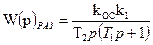. (7.21)

Тогда передаточная функция регулятора в соответствие с (7.6) определяется из выражения:

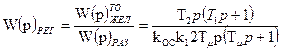. (7.22)

Считая, что постоянная времени T₁ невелика, и принимая T₁ = T_m , получается передаточная функция П–регулятора:

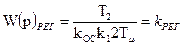. (7.23)

Уровень ограничения сигнала управления на выходе регулятора рассчитывается согласно выражению (7.14).

Настроенная таким образом система является астатической по отношению к задающему воздействию. При подаче возмущающего воздействия возникает статическая ошибка регулирования:

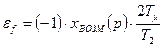. (7.24)

2.2. Настройка САУ с использованием ПИ – регулятора

Если динамика САУ (рисунок 7.5) характеризуется постоянной времени Т₁ и интегральной постоянной времени Т₂, то такая система обладает астатизмом первого порядка и является астатической по отношению к задающему воздействию. Если необходимо обеспечить астатизм и по отношению к возмущающему воздействию, то проводиться настройка системы на симметричный оптимум с применением ПИ – регулятора.

Передаточная функция САУ в разомкнутом состоянии будет иметь следующий вид:

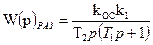. (7.25)

Тогда передаточная функция регулятора определиться:

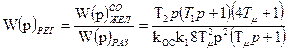. (7.26)

Считая, что постоянная времени T₁ невелика, и принимая T₁ = T_m , получается передаточная функция ПИ – регулятора:

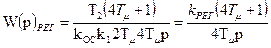. (7.27)

Уровень ограничения сигнала управления на выходе регулятора рассчитывается согласно выражению (7.14).

Настроенная на симметричный оптимум система будет астатической по отношению к задающему и возмущающему воздействию.

2.3. Провести моделирование системы управления в пакете System View с П и ПИ – регулятором. Рассчитать переходную характеристику x_ВЫХ(t) при подаче на вход системы единичного ступенчатого воздействия x_З(t) = 1(t), а также при подаче скачком возмущающего воздействия x_ВОЗМ(t) = 1(t).

2.4. Проанализировать полученные переходные процессы и определить показатели качества регулирования: статическую ошибку регулирования e, перерегулирование s, время регулирования t_Р, время переходного процесса t_ПП и колебательность M.

Содержание отчёта

1. Структурные схемы САУ.

2. Расчет передаточных функций регуляторов.

3. Структурные схемы моделей САУ с различными типами регуляторов.

4. Графики переходных процессов.

5. Инженерный анализ полученных переходных процессов.