Через его квадратурные компоненты
Любой действительный сигнал 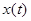 можно записать в виде
можно записать в виде 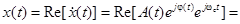
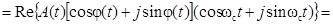
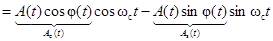 .
.
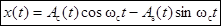 ,
,
где 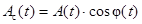 – косинусная,
– косинусная,
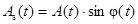 – синусная
– синусная
квадратурные компоненты сигнала 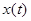 ,
,
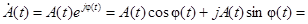
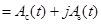 – комплексная огибающая.
– комплексная огибающая.
Представление 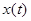 через квадратурные компоненты особенно полезно для узкополосных сигналов, у которых они оказываются медленно меняющимися функциями по сравнению с
через квадратурные компоненты особенно полезно для узкополосных сигналов, у которых они оказываются медленно меняющимися функциями по сравнению с 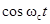 (при выборе
(при выборе 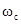 внутри спектра сигнала
внутри спектра сигнала 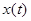 ). Формально условие узкополосности сигнала «в расширенном смысле» можно записать следующим образом
). Формально условие узкополосности сигнала «в расширенном смысле» можно записать следующим образом
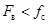 , где
, где 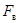 – верхняя частота в спектре
– верхняя частота в спектре 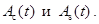
Обработку узкополосных сигналов можно выполнить проще и точнее через обработку их квадратурных компонентов. Действительно, если выполняется условие узкополосности сигнала, то спектр комплексного сигнала вида
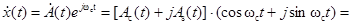
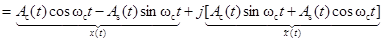 ,
,
получаемого сдвигом спектра огибающей 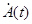 вверх на
вверх на 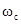 полностью располагается в области положительных частот, следовательно этот сигнал – аналитический и его мнимая часть является преобразованием Гильберта действительной части
полностью располагается в области положительных частот, следовательно этот сигнал – аналитический и его мнимая часть является преобразованием Гильберта действительной части
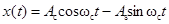
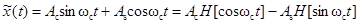 .
.
Таким образом, можно считать, что преобразование Гильберта узкополосного сигнала сводится к сдвигу фаз на угол –90° гармонических колебаний 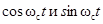 и не затрагивает его квадратурных компонентов.
и не затрагивает его квадратурных компонентов.





 На рис 2.10 приведена векторная диаграмма аналитического сигнала. Она представляет собой комплексную плоскость с вращающим-ся и меняющим свою длину вектором
На рис 2.10 приведена векторная диаграмма аналитического сигнала. Она представляет собой комплексную плоскость с вращающим-ся и меняющим свою длину вектором 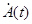 .
.
Угловая скорость его вращения изменяется во времени по закону
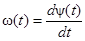 .
.
Контрольные вопросы
1. Как выглядит квазигармоническая форма записи произвольного сигнала 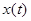 ?
?
2. Как определяют огибающую, фазу и мгновенную частоту сигнала 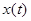 ?
?
3. Почему задача определения огибающей и фазы сигналов не является однозначной?
4. Какой сигнал называют аналитическим?
5. В чём заключается преобразование Гильберта в частотной области?
6. Как схемотехнически реализуют преобразование Гильберта?
7. Напишите выражение передаточной функции преобразователя Гильберта.
8. Какова импульсная характеристика преобразователя Гильберта?
9. Напишите аналитическое выражение преобразования Гильберта во временной области.
10. Чем обратное преобразование Гильберта отличается от прямого?
11. Какая связь аналитического сигнала с символическим изображением гармонического колебания, используемым в символическом методе.
12. Каковы особенности спектра аналитического сигнала?
13. Как изменяется аналитический сигнал при сдвиге фаз всех его спектральных составляющих на один и тот же угол j?
14. Как с помощью аналитического сигнала записать операцию смещения спектра сигнала на Dw?
15. Что называют квадратурными компонентами сигнала?
16. Запишите аналитическое выражение сигнала 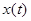 через его квадратурные компоненты.
через его квадратурные компоненты.
17. Как огибающая и фаза сигнала связаны с его квадратурными компонентами?
18. Почему обработку узкополосных сигналов проще и точнее реализуют через их квадратурные компоненты?
19. Что представляет собой векторная диаграмма аналитического сигнала?
