Рекомендации к выполнению задания

При выполнении пунктов 1–6 задания используется аппарат векторной алгебры, решение пунктов

7–10 основано на применении уравнений прямой и плоскости в пространстве.

Пример решения задачи

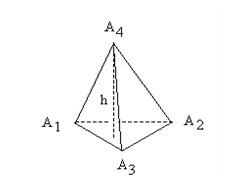Даны координаты вершин пирамиды:

А₁ (2, 4, –3),

А₂ (5, 6, 3),

А₃ (–2,7,–3),

А₄ (4, 1, 0).

Решение:

Найдем длину ребра А₁А₂ как модуль вектора:

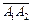={x₂ – x₁, y₂ – y₁, z₂ – z₁} =

= {5 – 2, 6 – 4, 3 – (–3)} = {3; 2; 6}

.

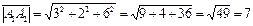Угол между ребрами А₁А₂ и А₁А₄ найдем как угол между векторами 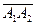= {3; 2; 6} и 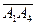= {4 – 2, 1 – 4, 0 – (–3)} = {2, –3, 3}, используя скалярное произведение векторов:

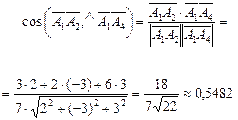
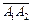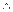
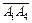( , ) = arccos 0,5482 = 56°46¢.

3. Проекцию ребра А₁А₃ на ребро А₁А₂ найдем как проекцию вектора 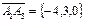на вектор :

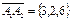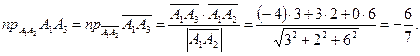
4. Площадь грани А₁А₂А₃ можно вычислить, используя геометрический смысл векторного произведения векторов (см. пункт в) справочного материала). Найдем векторное произведение векторов

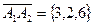и = :

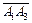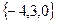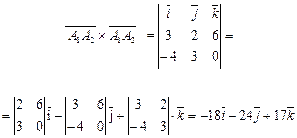
и его модуль:

.

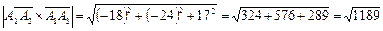Модуль векторного произведения векторов 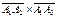равен площади параллелограмма, построенного на векторах 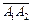и 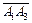как на сторонах, а площадь грани А₁А₂А₃ составляет половину площади этого параллелограмма, т.е.

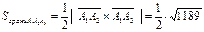(кв. ед.).

5. Длину высоты грани А₁А₂А₃, опущенной из вершины А₃ на ребро А₁А₂ , найдем по формуле

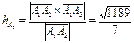
6. Объем пирамиды А₁А₂А₃А₄ можно вычислить, используя геометрический смысл смешанного произведения векторов (см. пункт г) справочного материала). Найдем смешанное произведение векторов
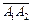= {3; 2; 6}, 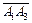= {–4, 3, 0} = {2, –3, 3}:

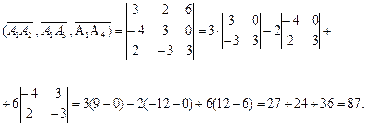
Модуль смешанного произведения векторов ( , , 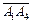) равен объему параллелепипеда, построенного на векторах 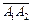, , 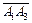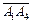как на сторонах, а объем пирамиды А₁А₂А₃А₄ составляет шестую часть объема этого параллелепипеда, т.е.

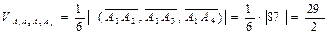(куб. ед.).

7. Для составления уравнения прямой А₁А₃ воспользуемся уравнением (5) прямой, проходящей через две данные точки А₁(2,4,–3) и А₃(–2, 7, –3).

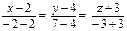
или

А₁А₃: .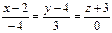

8. Составим уравнение плоскости А₁А₂А₃. Поскольку плоскость П проходит через три точки

А₁(2, 4, –3), А₂(5, 6, 3), А₃(–2, 7, –3), то согласно (2) получим:

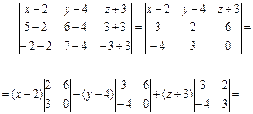
= –18(x – 2) – 24(у -4) + 17(z + 3) = 0

или

18х + 24у – 17z –183 = 0.

9. Угол между ребром А₁А₄ и гранью А₁А₂А₃ найдем по формуле (6) как угол между прямой А₁А₄ и плоскостью П. Направляющий вектор прямой А₁А₄ есть вектор 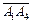= {2, –3, 3} (см. пункт 4), нормальный вектор плоскости А₁А₂А₃ согласно (1) 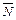= {18, 24, –17} (см. пункт 6).

Тогда:

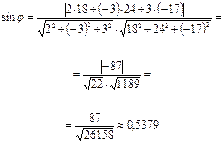
j = arcsin 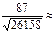arcsin 0,5379 » 32°33¢.

10. Составим уравнение высоты h, опущенной на грань А₁А₂А₃ из вершины А₄. Известны координаты точки А₄(4, 1, 0), через которую проходит эта прямая, искомая прямая имеет направляющий вектор , параллельный нормальному вектору 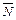= {18, 24, –17} плоскости П грани А₁А₂А₃. Тогда согласно (4) канонические уравнения искомой прямой:

.

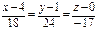Значение h по формуле (3) будет равно

.

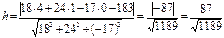Ответ:

1) 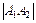= 7; 2)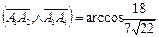 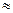56°46¢;

3) 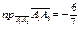4) 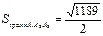(кв. ед.); 5)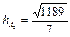

6) 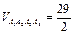(куб. ед.); 7) А₁А₃ : ;

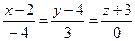8) П : 18х + 24у + 17z – 183 = 0; 9) 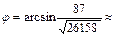32°33¢;

10) .

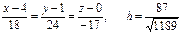Условия задачи 2.

№ варианта	А1	А2	А3	А4
	(0, 4, 3)	(1,4,0)	(–1,–1,0)	(4, 1, 2)
	(1, 2, –1)	(2,0,0)	(0,–1,4)	(1,2,4)
	(1, –2, 0)	(3,1,5)	(3,–3,1)	(2,–1,0)
	(2, –1, 3)	(3, 0,2)	(2,0,–3)	(3,2,1)
	(3, –1, 0)	(–1,1,–3)	(1,–1,5)	(1,0,2)
	(1, 2, –3)	(0,–1,2)	(3,–1,–1)	(3,2,3)
	(2,1,3)	(–3,–4,0)	(4,2,1)	(1,–4,1)
	(3,–2,1)	(1,1,–1)	(–5,–1,3)	(3,4,1)
	(2,3,–1)	(–4,1,0)	(–1,–1,5)	(2,3,2)
	(–3,1,2)	(2,–1,4)	(4,1,1)	(2,1,–1)

Задача 3. Найти пределы функций.