Фундаментальное множество циклов графа
Предположим, нам нужно с помощью закона Кирхгофа составить систему линейных уравнений для электрической цепи. Цепь имеет сложную структуру и содержит большое количество циклов. Запишем закон Кирхгофа для каждого цикла и начнем решать полученную систему уравнений. Сразу обнаружится, что часть уравнений являются линейно зависимыми, т.е. получаются из других. Значит, какие-то циклы были не нужны?!
В этой главе будет доказано, что любой цикл графа можно однозначно разложить по фундаментальным циклам этого графа так же, как любой вектор трехмерного пространства однозначно представляется линейной комбинацией базисных векторов i, j, k. Так же будет показано, как построить для данного графа это фундаментальное множество.
В дальнейшем под графом будем понимать связный неориентированный граф, под циклом – элементарный цикл.
Вначале для произвольных множеств А и В введем операцию взятия симметрической разности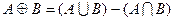 
(рис. 8.13, 8.14).
Рис. 8.13. Симметрическая разность двух множеств
Построим симметрическую разность трех множеств. Выберем порядок действий, соответствующий следующей расстановке скобок: (A B) C.
Рис. 8.14. Симметрическая разность трех множеств
В силу симметрии при любой расстановке скобок будет получаться то же множество A B C. Можно установить закономерность: в симметрическую разность входят элементы, содержащиеся одновременно либо в одном, либо в трех множествах, а принадлежащие двум,– удаляются. Обобщим этот результат на произвольное число множеств.
Утверждение 1
Симметрическая разность множеств А1, А2, …, Аk содержит в точности те элементы, которые принадлежат нечетному числу множеств.
Доказать это можно индукцией по числу множеств.
Вернемся к фундаментальным циклам. Это множество определяется через каркас графа.
Пусть уже построен каркас D=<V, T> графа G=<V, E>. Если к каркасу добавить произвольную хорду e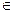 
(E-T), то получившийся граф (D 
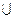e) будет содержать ровно один цикл. Назовем этот цикл Се (рис. 8.15). Добавляя к каркасу поочередно все хорды, получим фундаментальное множество циклов Ф относительно каркаса DФ = {Cе : e 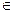(E-T)}.
Вопрос 1. Укажите фундаментальное множество циклов графа G относительно каркаса D на рис. 8.15.
Симметрическая разность любого числа циклов графа G является циклом графа G.
Вопрос 2. В графе G (см. рис. 8.15) найти C1 C2, если C1=(1–2–3), C2=(2–3–4).
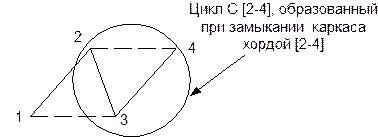
Рис. 8.15. Ф-цикл
Сформулируем без доказательства следующее утверждение.
Утверждение 2
Произвольный цикл C графа G можно однозначно представить как симметрическую разность некоторого числа фундаментальных циклов.
Другими словами, любой цикл раскладывается по базису фундаментальных циклов.
Как уже говорилось, знание фундаментальных циклов имеет существенное значение при анализе электрических цепей. Для каждого фундаментального цикла данной цепи можно записать закон Кирхгофа: сумма падений напряжений вдоль цикла равна 0. Все эти уравнения независимы, уравнения для остальных циклов будут следовать из них.
Опишем простой алгоритм построения фундаментальных циклов. Он основан на поиске в глубину из произвольного корня k и является рекурсивным. Каждая встреченная новая вершина v помещается в СТЕК и получает номер GLN[v] (порядок просмотра) и удаляется из него после использования. Поэтому СТЕК всегда содержит последовательность вершин от рассматриваемой в данный момент вершины v до корня k.
Анализируемое алгоритмом ребро (v–u) будет замыкать цикл, если (v–u) – хорда.
Критерий хорды следующий:
(v–u) будет хордой, если u – найденная соседка v – уже встречалась раньше при поиске в глубину. В этом случае она находится в СТЕКе и ее номер GLN(u) меньше соответствующего номера GLN(v). Но это еще не все. Если из u мы попали в вершину v, т. е. u является отцом v, то GLN(u) < GLN(v), но (v–u) не хорда, а ветвь каркаса. Эту ситуацию легко распознать, так как в этом случае вершины u и v стоят в СТЕКе рядом.
Если же GLN(u) < GLN(v) и u не является отцом v, то (v–u) – хорда и цикл состоит из верхней группы элементов стека, начиная с v и кончая u (рис. 8.16).
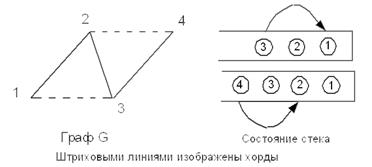
Рис. 8.16. Стек, содержащий фундаментальный цикл
Мы заранее знаем, что наибольшее число вершин, одновременно находящихся в стеке, не превышает n – длины пути от корня до самой удаленной вершины, поэтому стек можно имитировать массивом переменной длины (длина его будет колебаться от 0 до n). Текущее значение длины будет храниться в переменной d, вталкивание в стек вершины v будет изображаться: СТЕК[d]:= v, выталкивание верхушки СТЕКА: d:= d-1.
АЛГОРИТМ {Нахождение множества Ф-циклов графа}
Данные: Граф G=<V, E>, представленный списками ЗАПИСЬ[v], v 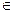V.
Результаты: Множество фундаментальных циклов Ф графа G.
Переменные: d, num, СТЕК, ЗАПИСЬ, GLN – глобальные.
1 procedure CYCLE(v);
{находит фундаментальное множество циклов для компоненты связности графа, содержащей вершину v}
2 begin
3 d:= d+1; СТЕК[d]:= v;
4 num:= num+1; GLN[v]:= num;
5 for u 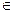ЗАПИСЬ[v] do
6 if GLN[u]=0 then
7 CYCLE(u) {для новой вершины u}
8 else if (u<>СТЕК[d-1]) AND (GLN[u]<GLN[v]) then
9 печать СТЕК[d],СТЕК[d-1],..,СТЕК[c]=u;
{ребро (v-u) замкнуло новый цикл}
10 d:= d-1; {использованная v удаляется из стека}
11 end;
1 begin {основная программа}
2 for v Є V do GLN[v]:= 0;
3 num:= 0; {инициализация перед началом нумерации}
3 d:= 0; СТЕК[d]:= 0; {d – число элементов в стеке}
4 for v 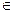V do
5 if GLN[v]=0 then CYCLE(v)
6 end.
Оценим вычислительную сложность алгоритма.
Если отбросить число шагов, требующих выписывания всех фундаментальных циклов (строки 8–9), сложность имеет порядок О(n+m), как у всех алгоритмов, основанных на поиске в глубину.
Число шагов, потраченное на печать всех фундаментальных циклов, пропорционально суммарной длине всех циклов. Количество фундаментальных циклов = число всех хорд = m - (n - 1) = m - n +1. Длина любого цикла не превосходит n. Таким образом, суммарная длина всех циклов не превосходит n(m - n + 1)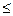 
mn + n. Если отбросить случай, когда число ребер m=0, то сложность равна
О(mn).
Ответ 1. Ф = {C1=(1–2–3), C2=(2–3–4)}.
Ответ 2. С1 С2=(1–2–3–4).