Цикломатическое число графа. Пространство циклов
Цикломатическим числом графа  называется число
называется число
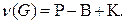 (6)
(6)
Это число обладает следующими свойствами:
1) 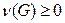 для любого графа
для любого графа 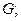
2) если 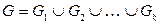 – разложение графа
– разложение графа  на компоненты связности, то
на компоненты связности, то 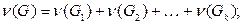
3) 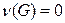
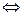
 – лес.
– лес.
Упражнение 3.18.Найти количество компонент связности леса, имеющего 18 вершин и 10 рёбер.
Решение. Пусть  – данный граф. Так как
– данный граф. Так как  – лес, то
– лес, то 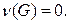 По формуле (6) получаем:
По формуле (6) получаем: 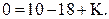 Отсюда
Отсюда 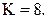 Таким образом,
Таким образом,  имеет 8 компонент связности.
имеет 8 компонент связности.
Упражнение 3.19. Сколько рёбер может быть у графа, имеющего 12 вершин и состоящего из 3 компонент связности?
Решение. Наименьшее количество рёбер можно получить из неравенства 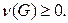 Имеем:
Имеем: 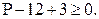 Отсюда
Отсюда 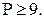 Ровно 9 рёбер будет у графа, все компоненты связности которого являются деревьями: например, если одна из компонент – цепь из 9 вершин, а две другие – изолированные точки.
Ровно 9 рёбер будет у графа, все компоненты связности которого являются деревьями: например, если одна из компонент – цепь из 9 вершин, а две другие – изолированные точки.
Найдём наибольшее значение Р. Начнём с общего рассуждения. Пусть, к примеру, граф  с
с 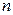 вершинами состоит из двух не соединяющихся между собой подграфов
вершинами состоит из двух не соединяющихся между собой подграфов 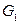 и
и 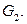 Если
Если 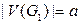 и
и 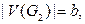 то наибольшее число рёбер графа
то наибольшее число рёбер графа  равно
равно 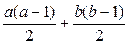 (это соответствует случаю, когда
(это соответствует случаю, когда 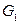 и
и 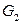 – полные графы. Так как
– полные графы. Так как 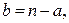 то наибольшее количество рёбер в
то наибольшее количество рёбер в  равно
равно 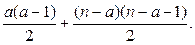 Это выражение является квадратичной функцией от
Это выражение является квадратичной функцией от 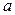 с положительным коэффициентом перед
с положительным коэффициентом перед 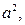 поэтому наибольшее значение эта функция будет принимать при крайних значениях
поэтому наибольшее значение эта функция будет принимать при крайних значениях 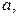 т.е. когда
т.е. когда 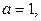
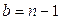 или
или 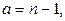
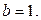 Аналогичный результат получится и в случае, когда граф
Аналогичный результат получится и в случае, когда граф  разбивается на 3 или большее число частей. В нашем случае наибольшее число рёбер у графа
разбивается на 3 или большее число частей. В нашем случае наибольшее число рёбер у графа  будет, когда одна компонента связности – полный граф с 10 вершинами, а две другие – изолированные точки. В этом случае число рёбер равно
будет, когда одна компонента связности – полный граф с 10 вершинами, а две другие – изолированные точки. В этом случае число рёбер равно 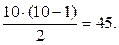 Таким образом, мы имеем:
Таким образом, мы имеем: 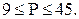 Покажем, что любое число из этого диапазона будет числом рёбер некоторого графа. Действительно, если одна компонента связности – цепь с 10 вершинами, а две другие – изолированные точки, то
Покажем, что любое число из этого диапазона будет числом рёбер некоторого графа. Действительно, если одна компонента связности – цепь с 10 вершинами, а две другие – изолированные точки, то 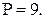 Возьмём эту цепь и будем добавлять к ней по одному ребру, пока не получится полный граф. Тогда количество рёбер будет принимать все значения 9, 10, …, 45.
Возьмём эту цепь и будем добавлять к ней по одному ребру, пока не получится полный граф. Тогда количество рёбер будет принимать все значения 9, 10, …, 45.
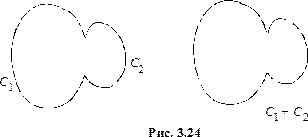 В этом разделе мы будем называть циклами как обычные циклы, так и объединения обычных циклов (иногда их называют “циклами” (в кавычках) или обобщёнными циклами). Сложение циклов осуществляется следующим образом: берём все рёбра, входящие в эти циклы, и удаляем общие рёбра (см. рис. 3.24).
В этом разделе мы будем называть циклами как обычные циклы, так и объединения обычных циклов (иногда их называют “циклами” (в кавычках) или обобщёнными циклами). Сложение циклов осуществляется следующим образом: берём все рёбра, входящие в эти циклы, и удаляем общие рёбра (см. рис. 3.24).
Пусть дан граф 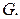 Тогда все циклы (в широком смысле) этого графа будут образовывать линейное пространство
Тогда все циклы (в широком смысле) этого графа будут образовывать линейное пространство 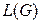 над полем
над полем 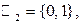 если рассматривать операцию сложения циклов и умножение на элементы поля
если рассматривать операцию сложения циклов и умножение на элементы поля 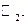
Определим теперь двоичную запись циклов графа. Пусть  – граф и
– граф и 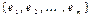 – все его рёбра. Тогда каждый цикл
– все его рёбра. Тогда каждый цикл 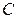 представляется в виде строчки из 0 и 1 длины
представляется в виде строчки из 0 и 1 длины 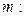
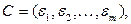 где
где
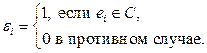
Нетрудно видеть, что сложение циклов при таком кодировании будет соответствовать покомпонентному сложению строк по модулю 2. Приведём пример. Пусть дан граф, изображённый на рисунке 3.25.
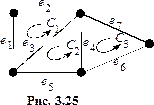 Рассмотрим его циклы
Рассмотрим его циклы 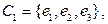
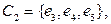
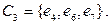 Так как в графе 7 рёбер, то циклы будут записываться в виде двоичных последовательностей длины 7. Так как
Так как в графе 7 рёбер, то циклы будут записываться в виде двоичных последовательностей длины 7. Так как 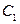 состоит из рёбер
состоит из рёбер 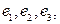 то в 1-й, 2-й и 3-й позициях будут стоять 1, а в остальных нули. Таким образом,
то в 1-й, 2-й и 3-й позициях будут стоять 1, а в остальных нули. Таким образом, 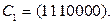 Аналогично получаем:
Аналогично получаем: 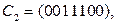
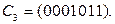 Сложим
Сложим 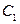 и
и 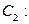
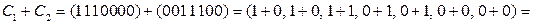
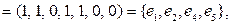
что соответствует правилу сложения циклов.
Рассмотрим теперь линейное пространство 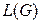 циклов графа
циклов графа 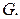 Так как граф
Так как граф  конечный, то пространство
конечный, то пространство 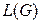 имеет конечный базис, т.е. совокупность циклов
имеет конечный базис, т.е. совокупность циклов 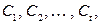 которые обладают свойствами:
которые обладают свойствами:
1) 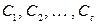 линейно независимы;
линейно независимы;
2) любой цикл 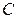 данного графа является линейной комбинацией циклов
данного графа является линейной комбинацией циклов 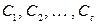 с коэффициентами 0 или 1:
с коэффициентами 0 или 1:
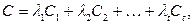
где 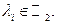 Число
Число 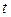 элементов базиса называется размерностью пространства
элементов базиса называется размерностью пространства 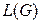 и обозначается
и обозначается 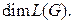 Оказывается, что число
Оказывается, что число 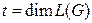 совпадает с цикломатическим числом графа.
совпадает с цикломатическим числом графа.
Теорема.Пусть  – граф и
– граф и 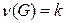 – его цикломатическое число. Тогда:
– его цикломатическое число. Тогда:
1) 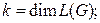
2) в графе  существуют
существуют 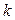 рёбер
рёбер 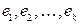 таких, удаление которых превращает
таких, удаление которых превращает  в лес, имеющий те же компоненты связности (по вершинам), что и граф
в лес, имеющий те же компоненты связности (по вершинам), что и граф 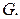
Для связного графа справедливо следующее утверждение.
Следствие. Если  – связный граф и
– связный граф и 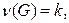 то в графе
то в графе  найдутся
найдутся 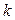 рёбер
рёбер 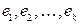 таких, что
таких, что 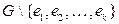 – дерево.
– дерево.
Дерево 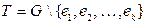 называется остовным деревом графа
называется остовным деревом графа 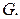 Остовное дерево выбирается неоднозначно. Например, в графе на рисунке 25
Остовное дерево выбирается неоднозначно. Например, в графе на рисунке 25 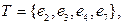
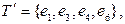
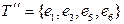 – остовные деревья.
– остовные деревья.
Приведём алгоритм построения базиса пространства 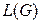 циклов графа
циклов графа 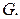 Пусть
Пусть 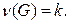
Если 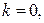 то
то  – лес, и искомый базис – пустое множество. Пусть
– лес, и искомый базис – пустое множество. Пусть 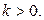 Тогда в
Тогда в  есть хотя бы один непустой цикл. Обозначим его через
есть хотя бы один непустой цикл. Обозначим его через 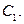 Возьмём любое ребро из этого цикла:
Возьмём любое ребро из этого цикла: 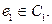 Удалим это ребро из графа
Удалим это ребро из графа 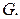 Получим граф
Получим граф 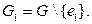 У него
У него 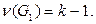 Если
Если 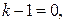 то
то 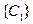 – базис пространства
– базис пространства 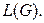 Если
Если 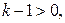 то находим в графе
то находим в графе 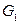 цикл
цикл 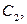 его ребро
его ребро 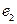 и т.д. В конце концов мы получим циклы
и т.д. В конце концов мы получим циклы 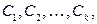 образующие базис пространства
образующие базис пространства 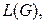 и рёбра
и рёбра 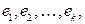 удовлетворяющие требуемым условиям.
удовлетворяющие требуемым условиям.
Упражнение 3.20. Построить базис пространства циклов графа 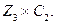
Решение. Граф 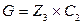 изображён на рисунке 5. Сделаем другой, более удобный рисунок 3.26.
изображён на рисунке 5. Сделаем другой, более удобный рисунок 3.26.
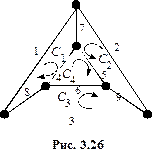 У этого графа
У этого графа 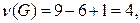 поэтому
поэтому 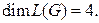 Следовательно, нам надо найти 4 базисных цикла. Проверим, что это будут циклы
Следовательно, нам надо найти 4 базисных цикла. Проверим, что это будут циклы 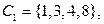
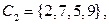
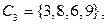
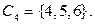 В двоичной записи
В двоичной записи 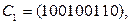
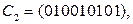
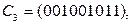
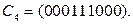 Составим из координат этих векторов матрицу
Составим из координат этих векторов матрицу
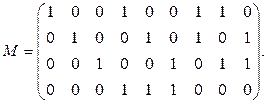
Минор этой матрицы, составленный из элементов первых 4 столбцов, равен
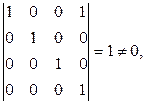
поэтому строки матрицы 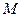 линейно независимы. Это означает, что векторы
линейно независимы. Это означает, что векторы 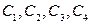 пространства
пространства 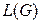 линейно независимы над полем
линейно независимы над полем 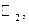 а так как размерность пространства
а так как размерность пространства 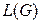 равна 4, то
равна 4, то 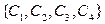 – его базис. Любой цикл является линейной комбинацией базисных. Например, если
– его базис. Любой цикл является линейной комбинацией базисных. Например, если 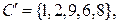 то
то 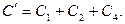
Упражнение 3.21.Сколько всего циклов имеет граф  у которого
у которого 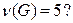
Решение. Пусть 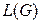 – пространство циклов. Тогда
– пространство циклов. Тогда 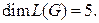 Таким образом, у графа
Таким образом, у графа  имеется 5 базисных циклов
имеется 5 базисных циклов 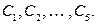 Все остальные циклы – линейные комбинации базисных с коэффициентами 0 или 1. Например,
Все остальные циклы – линейные комбинации базисных с коэффициентами 0 или 1. Например, 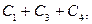
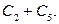 Общий вид циклов такой:
Общий вид циклов такой: 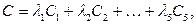 где
где 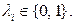 Значит, всего циклов
Значит, всего циклов 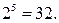 Среди них могут быть “ненастоящие” циклы, т.е. циклы, являющиеся объединениями простых циклов, и обязательно будет пустой цикл – цикл, у которого нет ни одного ребра.
Среди них могут быть “ненастоящие” циклы, т.е. циклы, являющиеся объединениями простых циклов, и обязательно будет пустой цикл – цикл, у которого нет ни одного ребра.
