Нахождение минимальных КНФ ФАЛ
Для нахождения минимальных КНФ можно рекомендовать два метода:
1.Метод Квайна, в основу которого берется операция склеивания конституент нуля функции. Конституентам нуля на карте Карно соответствуют пустые клетки (или клетки, содержащие нули). Правила склеивания конституент нуля аналогичны правилам склеивания конституент единицы.
2. Минимизация функции, инверсной заданной, и преобразование полученной минимальной ДНФ функции 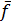 по законам инверсии и де Моргана в минимальную КНФ.
по законам инверсии и де Моргана в минимальную КНФ.
Пример 8. Найти минимальную КНФ ФАЛ, приведенной в примере 7.
Решение.
1. По первому методу выполняем склеивание конституент нуля функции, которая нанесена на карту Карно (рис. 4,б). Склеивание конституент нуля функции, которые на рис. 4,б отмечены точками, образуют три простых дизъюнкции 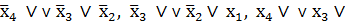
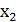 третьего ранга. На карте ясно видно, что эти простые дизъюнкции являются так же существенными, т.е. должны обязательно войти в минимальную КНФ функции. Другими простыми дизъюнкциями третьего ранга являются
третьего ранга. На карте ясно видно, что эти простые дизъюнкции являются так же существенными, т.е. должны обязательно войти в минимальную КНФ функции. Другими простыми дизъюнкциями третьего ранга являются 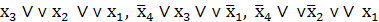 . Так как полученные простые
. Так как полученные простые  дизъюнкции третьего ранга не склеиваются , то простых дизъюнкций второго ранга нет.
дизъюнкции третьего ранга не склеиваются , то простых дизъюнкций второго ранга нет.
2. Составляем таблицу (табл.6), столбцы которой отмечаем конституентами нуля 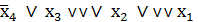 и
и 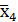 ∨
∨ 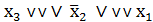 , а строки - простыми дизъюнкциями
, а строки - простыми дизъюнкциями  ∨
∨ 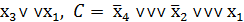 и расставляем метки.
и расставляем метки.
Таблица 6
 | 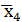 ˅ ˅ 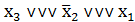 | |
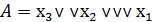 | * | |
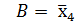 ˅ ˅  | * | * |
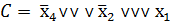 | * |
3. Находим тупиковые и минимальные КНФ.
Составляем конъюнкцию простых дизъюнкций отдельных столбцов (по способу Петрика): (A ∨ B)(B ∨ C).
Применяя распределительный закон (раскрытие скобок в данном случае происходит одновременно), получим (A ∨ B)(B ∨ C) = B ∨ AC. Учитывая существенные дизъюнкции
D= 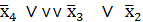 , E =
, E = 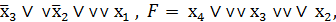 получим:
получим:
(B ∨ AC)DEF = BDEF ∨ ACDEF. (12)
Из выражения (12) следует, что функция имеет две тупиковых формы:
fтуп1(х4, х3, х2, х1) = BDEF =
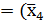 ˅
˅  ;
;
fтуп2(х4, х3, х2, х1) = ACDEF = =( 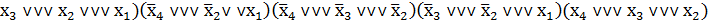 .
.
Минимальной является первая тупиковая форма:
fмин(х4, х3, х2, х1) = 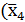 ˅
˅ 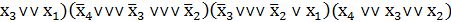 .
.
Примечание: минимальную КНФ функции можно сразу найти, анализируя карту Карно на рис. 4,б. Оставшиеся неотмеченными точками две конституенты нуля склеиваются по переменной 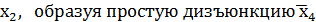 ˅
˅ 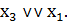 Конъюнкция последней и существенных дизъюнкций и есть минимальная КНФ.
Конъюнкция последней и существенных дизъюнкций и есть минимальная КНФ.
Минимальную КНФ можно найти вторым способом, минимизируя функцию 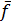 (х4, х3, х2, х1), карта Карно которой показана на рис. 4,в:
(х4, х3, х2, х1), карта Карно которой показана на рис. 4,в:
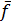 мин(х4, х3, х2, х1) =
мин(х4, х3, х2, х1) = 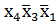 ∨
∨ 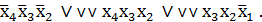 (13)
(13)
Инвертируя левую и правую части выражения (13) и применяя правило де Моргана , получим минимальную КНФ:
fмин (х4, х3, х2, х1) = 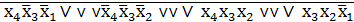 =
=
 ∨
∨ 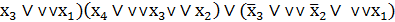 . (14)
. (14)
Преобразование минимальных ДНФ и КНФ в базисы функций И-НЕ и ИЛИ-НЕ
Дважды инвертируя правые части выражений (10) и (14) и применяя правило де Моргана, получим минимальные формы функции fмин (х4, х3, х2, х1) в базисах функций И-НЕ и ИЛИ-НЕ:
fмин (х4, х3, х2, х1) = 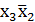 ∨
∨ 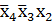 ∨
∨ 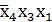 ∨
∨ 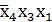 =
=
= 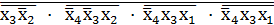 ; (15)
; (15)
fмин (х4, х3, х2, х1) = 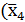 ˅
˅ 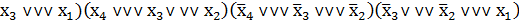 =
=
= 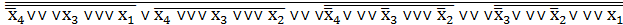 . (16)
. (16)
