Фармакокинетическая модель

Рассмотрим модель, описывающую кинематику распределения введенных в организм препаратов (лекарств). Будем считать, что терапевтический эффект зависит от концентрации препарата в больном органе (органе-мишени) и времени нахождения лекарства в действующей концентрации. Модель должна дать ответ о дозе лекарства, пути и периодичности введения, которое обеспечивало бы достаточный терапевтический эффект при минимальном побочном действии.

Из физиологии известно, что концентрация препарата в органе может зависеть от ряда процессов, скорости которых характеризуются константами К:

1). Всасывание препарата в кровяное русло при внесосудистом введении – константа - К₁₂.

2). Транспорт препарата из крови в органы - К₂₃.

3). Транспорт препарата из органа в кровь – К₃₂.

К12

К23

К32

Кровь

Кишечник Кожа Мышцы

Орган мишень

4). Удаление (элиминация) препарата из крови почками и разрушение его печенью – К₄.

Всякая модель предполагает упрощение реальных процессов. В этой модели рассматривается только кинетика, т.е. течение во времени всех процессов без выяснения их причин. Организм представляется в виде отдельных простых блоков (кровь, орган-мишень, органы, элиминирующие препарат) – фармакокинетических камер т.е. частей системы, в пределах каждой из которых распределение препарата предполагается равномерным. Есть еще целый ряд упрощений. Например, не учитывается периодичность в чувствительности и функционировании органов, влияние препарата на органы и т.д. Но все это позволяет описывать изменение концентрации препарата в блоках простыми линейными дифференциальными уравнениями. Например, небольшое изменение (убыль) концентрации препарата dC₁ в первом блоке после введения за время dt:

dC₁= -K₁₂C₁dt

Заметим, что каким бы сложным ни был процесс, всегда можно выделить такой малый промежуток времени, в течение которого процесс будет линейным.

Учитывая поступление и введение препарата в блоках, для скоростей изменения концентраций получим систему уравнений

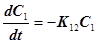
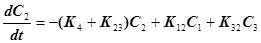
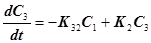
Всегда решаются, т.е. интегрируются, только дифференциальные уравнения первой степени, к которым и стараются свести путем преобразований и упрощений системы из нескольких уравнений.

Один из способов упрощения системы – объединение нескольких блоков в один или удаление несущественных элементов.

Другой способ – рассматривать часть системы как стационарную, тогда в этой части системы 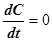и дифференциальное уравнение превращается в алгебраическое.

Рассмотрим более простую систему. Допустим, что препарат непрерывно со скоростью 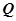поступает в кровь, тогда изменение его количества в крови.

,

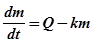где k – константа удаления препарата из крови

Предположим, что в момент t=0, масса препарата в крови m=0.

Тогда можно проинтегрировать дифференциальное уравнение, предварительно разделив переменные, и найти его частное решение.

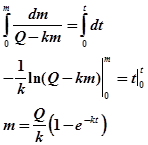
Для получения зависимости C(t) разделим обе части уравнения на объем V, в котором распределяется препарат.

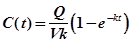
При 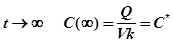См. график.

Из решения видно, что для достижения в крови некоторой постоянной концентрации препарата C^* его следует вводить со скоростью

Q=C*Vk

Время достижения уровня С* будет также будет зависеть от константы скорости выведения препарата k. Таким образом, совершенно очевидно, что лечебная концентрация препарата в крови устанавливается не мгновенно, как хотелось бы в лечебных целях, а по прошествии некоторого времени 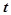. Можно для более быстрого достижения уровня С* сочетать непрерывное введнние препарата с начальным разовым введением некоторой нагрузочной дозы m_n.

Нагрузочная доза препарата в крови будет уменьшаться по закону

,

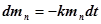из которого следует закон изменения количества препарата со временем.

^.

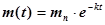Объединяя оба процесса, получим для изменения концентрации

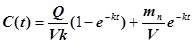или .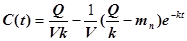

Из последнего уравнения видно, что конечный уровень концентрации препарата, т.е. при 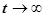по-прежнему равен С* и не зависит от нагрузочной дозы.

Скорость достижения уровня С* зависит от величины 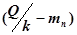, т.е. нагрузочная доза для мгновенного достижения уровня С* может быть получена из равенства 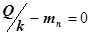. Она равна

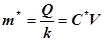
Таким образом для мгновенного создания в крови желаемой концентрации С^* необходимо ввести нагрузочную дозу m* и вести инфузию со скоростью Q=C*Vk.

Этот теоретический вывод был подтвержден экспериментально, что и является решающей проверкой правильности модели.

Более сложные модели можно построить путем суммирования блоков, если мы будем оставаться в рамках линейного приближения, т.е. описывать ситуацию линейными дифференциальными уравнениями.