Примеры упражнений и задач
Кафедра физики и высшей математики
| Дистанционное обучение | Физ. мат. 5. 11.2202 очн.плн. Физ. мат. 5. 11.2202 очн. скр |
Ю.А. Зуев
«Алгебра и геометрия»
Учебно-методические указания
По проведению практических занятий для студентов специальности 230102 (2202) всех форм обучения.
Www.msta.ru
Москва – 2005
УДК 519.6
Ó Зуев Ю.А. Алгебра и геометрия. Учебно-методические указания по проведению практических занятий для студентов специальности 230102(2202) всех форм обучения. М., МГУТУ, 2005.
В пособии сформулированы основные задачи практических занятий по алгебре и геометрии, определены темы каждого из 14 занятий и приведены примеры решаемых на них задач.
Автор: д.ф.-м.н., профессор Зуев Юрий Анатольевич
Рецензент: доцент Бартеньева Т.М.
Редактор: Свешникова Н.И.
ÓМосковский государственный университет технологий и управления, 2005
109004, Москва, Земляной вал, 73.
Содержание
Векторы на плоскости и в пространстве.………………….…4
Метод Гаусса решения систем линейных уравнений….......5
Определители 2-ого и 3-его порядков………………….…....5
Определители n-ого порядка. Матричная алгебра…….…...6
Комплексные числа……………………………………….…….7
Линейные преобразования и матрицы……………….……....8
Собственные векторы и собственные значения……….……8
Поверхности и кривые 2-ого порядка………………………..9
Конечные поля. Примитивные элементы…………………....9
Рекомендуемая литература…………………………………...10
1. Основные задачи практических занятий
Задачей практических занятий является закрепление начитанного на лекциях теоретического материала путем самостоятельного решения предлагаемых преподавателем задач, развитие у учащихся инициативы и творческих способностей. По плану на практические занятия по алгебре и геометрии выделено 54 часа. Эти часы предполагается использовать для решения систем линейных уравнений, матричную алгебру, аналитическую геометрию на плоскости и в пространстве, теорию линейных преобразований и квадратичных форм, а также для освоения элементов высшей алгебры: теории групп, колец и полей.
Занятие 1 (4 часа)
Тема: Векторы на плоскости и в пространстве. Линейные операции над векторами.
Примеры уравнений и задач.
1) На плоскости даны два вектора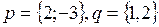 
. Найти разложение вектора 
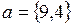по базису 
.
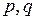2) Даны три вектора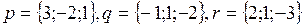 
. Найти разложение вектора 
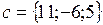по базису 
.
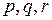3) Определить, при каких значениях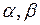 
векторы 
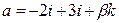и 
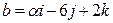коллинеарны.
Занятие 2 (4 часа)
Тема: Скалярное произведение векторов. Ортогональность.
Примеры уравнений и задач.
1) Даны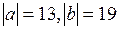 
и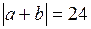 
.
Вычислить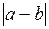 
.
2) Векторы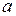 
и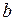 
взаимно перпендикулярны, причем 
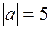и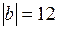 
.
Определить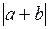 
и .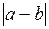
3) Доказать, что вектор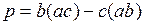 
перпендикулярен к вектору .
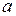4) Определить, при каком значении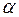 
векторы 
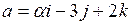и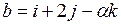 
взаимно перпендикуляры.
Занятие 3 (4 часа)
Тема: Метод Гаусса решения систем линейных уравнений. Системы однородные и неоднородные, совместные, определенные, неопределенные, несовместные.
Примеры упражнений и задач.
1) Решить систему уравнений:
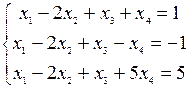
2) Подобрать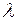 
так, чтобы система уравнений имела решение:
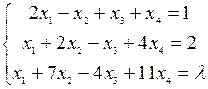
3) Решить системы уравнений:
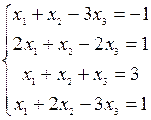
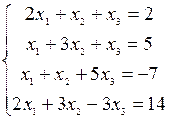
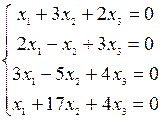
Занятие 4 (4 часа)
Тема: Определители 2-ого и 3-его порядков. Правило Крамера. Примеры упражнений и задач.
1) Вычислить определители:
; 
; 
.
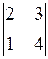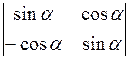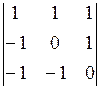2) Решить системы уравнений с помощью правила Крамера:
; 
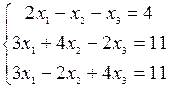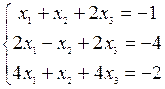
Занятие 5 (4 часа)