Интервалы для параметров нормального распределения

Пусть х₁, … ,х_n - выборка из нормального N(a,s²) распределения; значения среднего а и дисперсии s² неизвестны. Оценки для а и s²:

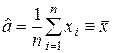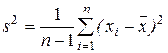, . (7)

Как известно, доверительным интервалом для среднего а с уровнем доверия Р_Д при неизвестной дисперсии является интервал

I(x) = (a₁(х), a₂(х) ),(8)

где 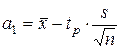, , 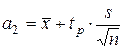(9)

t_p - квантиль порядка (1+ Р_Д)/2 распределения Стьюдента с n-1 степенями свободы.

Доверительным интервалом для стандартного отклонения s с уровнем доверия Р_Д является интервал

I (x)=(s₁(х), s₂(х)) , (10)

где 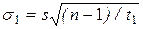, , 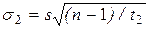(11)

t₁ и t₂- квантили порядков соответственно (1+ Р_Д)/2 и (1- Р_Д)/2 распределения хи-квадрат с n-1 степенями свободы.

Сгенерируем выборку объема n=20 из нормального распределения с параметрами a =10, s²=2²=4 и определим доверительные интервалы для a и s с уровнем доверия Р_Д : 0.8 , 0.9 , 0.95 , 0.98 , 0.99 , 0.995 , 0.998 , 0.999. Результаты выпишем в виде таблицы. C ростом Р_Д интервал расширяется, с ростом n - уменьшается.

Выполнение см. в пп. 2 - 4.

Если нас интересуют не интервалы, а верхние или нижние доверительные границы, то, как известно, они определяются теми же формулами (9) и (11). Например, нижней доверительной границей для a с уровнем доверия Р_Д является значение

,

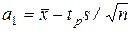где t_p - квантиль порядка Р_Д распределения Стьюдента с n-1 степенями свободы, а верхней границей для s с уровнем доверия Р_Д является

,

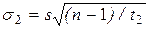где t₂ - квантиль порядка 1- Р_Драспределения хи-квадрат с n-1 степенями свободы.

Задание: определить верхние доверительные границы для а и s с уровнем доверия Р_Д= 0.95 .

Задание на самостоятельную работу

1) для заданной задачи построить оценку заданным методом (варианты заданий см. ниже);

2) построить доверительный интервал, основанный на этой оценке;

3) сгенерировать выборку заданного объема;

4) вычислить доверительный интервал.

Отчет по работе должен содержать:

постановки вопросов, формулы,

графики испытания доверительного интервала для 2-х случаев: с известной и неизвестной дисперсией (по п. 1.2),

таблицу доверительных интервалов для различных Р_Д (по п. 1.3),

вывод формул для оценок и интервалов, сгенерированную выборку и вычисленный интервал (по п. 1.4) .

Варианты задач.

Задача1.Расстояние а до некоторого объекта измерялось n₁ раз одним прибором и n₂- вторым; результаты х₁,…,х_n1; y₁,…,y_n2. Оба прибора при каждом измерении дают независимые случайные ошибки, нормально распределенные со средним 0 и стандартными отклонениями s₁ и s₂ соответственно. Методом максимального правдоподобия построить оценку a для а и доверительный интервал с уровнем доверия Р_Д .

Варианты исходных данных

¹	n1	n2	s1, êì	s2, êì	Ðä	a, êì
					0.95
					0.98
					0.95
					0.98
					0.95
					0.98
					0.95
					0.98
					0.95

измерения получить моделированием с заданным параметром а.

Решение(без вывода). Оценка

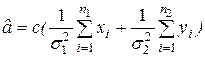, где с= ;

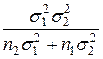доверительный интервал

I=( , ),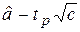

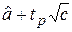где 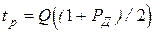- квантиль порядка (1+Р_Д)/2 распределения N(0,1).

Задача 2.Изготовлена большая партия из N=10000 приборов. Известно, что время безотказной работы случайно и распределено по показательному закону с плотностью

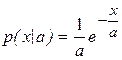, x ³ 0

С целью определения значения параметра а этой партии были поставлены на испытания n приборов; времена безотказной работы оказались равными х₁,…,х_n. Методом моментов построить оценку для а и доверительный интервал с уровнем доверия Р_Д. Кроме того, построить доверительный интервал для числа М приборов, имеющих время безотказной работы менее 50 часов.

Варианты исходных данных

n
ÐД	0.95	0.99	0.95	0.99	0.95	0.99	0.95	0.99	0.95
à

измерения получить моделированием с заданным параметром а.

Решение (без вывода). Оценка

;

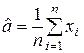доверительный интервал для а

I_a = ( , ),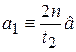

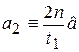где t₁=Q(2n, (1-Р_Д)/2), t₂=Q(2n, (1+Р_Д)/2) - квантили распределения хи-квадрат с 2n степенями свободы; доверительный интервал для М

I_M = ( N(1- exp(- 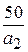)), N(1- exp(- )) ).

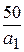Задача 3.Некоторое неизвестное расстояние а измерялось с аддитивной случайной ошибкой e , распределенной по закону Коши с плотностью

p_e( x ) = 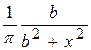, - ¥ < x < ¥.

По результатам х₁,…,х_n независимых измерений методом порядковых статистик построить оценку для а и приближенный доверительный интервал с коэффициентом доверия Р_Д .

Варианты исходных данных

n
b
ÐД	0.95	0.98	0.95	0.98	0.96	0.98	0.95	0.98	0.95
a

измерения получить моделированием с заданным параметром а.

Решение(без вывода).Оценкой для а является выборочная медиана - порядковая статистика с номером[n/2]+1

,

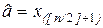или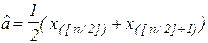

(у этих статистик асимптотические свойства одинаковы). Приближенный доверительный интервал, основанный на асимптотическом распределении выборочной р-квантили

I=( ),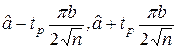

где t_p=Q((1+Р_Д)/2) - квантиль порядка (1+Р_Д)/2 распределения N(0,1).

Задача 4. В водоеме обитает некоторая биологическая популяция, состоящая из смеси особей двух возрастов. Длина особи - случайная величина, распределенная по нормальному закону N( a_i, s_i² ), где i=1,2 - индекс, относящийся к возрасту. С целью определения доли q особей 1-го возраста проведен отлов n особей и измерена их длина. По результатам х₁,…,х_n методом моментов построить оценку 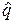для q и приближенный доверительный интервал с уровнем доверия Р_Д . Построить гистограмму наблюдений.

Варианты исходных данных

n
à1
à2
ÐÄ	0.95	0.95	0.98	0.95	0.95	0.98	0.95	0.95	0.98
q	0.5	0.4	0.3	0.5	0.4	0.3	0.5	0.4	0.3

Принять s₁=1см, s₂=1см. измерения получить моделированием с заданным значением q.

Решение (без вывода):

I = ( q₁, q₂ ),

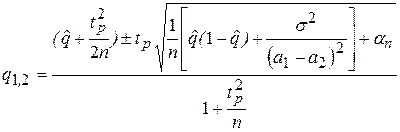, a_n º ,

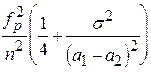t_p- квантиль порядка (1+ Р_Д)/2 для N(0,1).