Исходные данные задачи №1.02
| Бригада | Производительность бригад, шт/ч | Фонд рабочего времени, ч | |
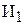 | 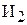 | ||
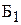 | 9,5 | ||
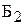 | |||
| Заказ, шт |
Ограничения по заказу изделий имеют следующую содержательную форму записи
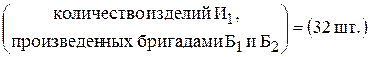
и
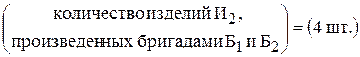 .
.
Математическая форма записи имеет вид
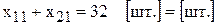 и
и
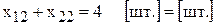 .
.
Ограничение по фондам времени имеет содержательную форму
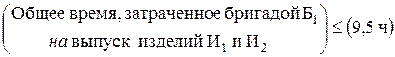
и
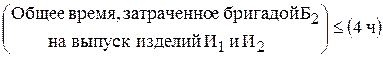 .
.
Проблема заключается в том, что в условии задачи прямо не задано время, которое тратят бригады на выпуск одного изделия 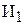 или
или 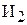 , т.е. не задана трудоемкость производства. Но имеется информация о производительности каждой бригады, т.е. о количестве производимых изделий в 1 ч. Трудоемкость Тр и производительность Пр являются обратными величинами, т.е.
, т.е. не задана трудоемкость производства. Но имеется информация о производительности каждой бригады, т.е. о количестве производимых изделий в 1 ч. Трудоемкость Тр и производительность Пр являются обратными величинами, т.е.
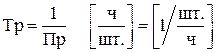 .
.
Поэтому используя табл.1.2, получаем следующую информацию:
® 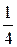 ч тратит бригада
ч тратит бригада 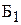 на производство одного изделия
на производство одного изделия 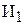 ;
;
® 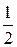 ч тратит бригада
ч тратит бригада 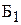 на производство одного изделия
на производство одного изделия 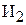 ;
;
® 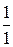 ч тратит бригада
ч тратит бригада 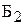 на производство одного изделия
на производство одного изделия 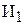 ;
;
® 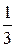 ч тратит бригада
ч тратит бригада 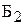 на производство одного изделия
на производство одного изделия 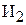 .
.
Запишем ограничения по фондам времени в математическом виде
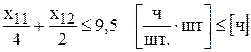
и
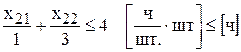 .
.
Неотрицательность объемов производства задается как
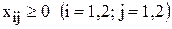 .
.
Таким образом, математическая модель этой задачи имеет вид
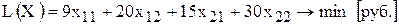 ,
,
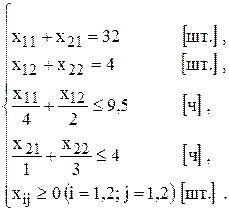
Задача №1.03*
Для пошива одного изделия требуется выкроить из ткани 6 деталей. На швейной фабрике были разработаны два варианта раскроя ткани. В табл.1.3 приведены характеристики вариантов раскроя 10 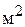 ткани и комплектность, т.е. количество деталей определенного вида, которые необходимы для пошива одного изделия. Ежемесячный запас ткани для пошива изделий данного типа составляет 405
ткани и комплектность, т.е. количество деталей определенного вида, которые необходимы для пошива одного изделия. Ежемесячный запас ткани для пошива изделий данного типа составляет 405 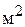 . В ближайший месяц планируется сшить 90 изделий.
. В ближайший месяц планируется сшить 90 изделий.
Постройте математическую модель задачи, позволяющую в ближайший месяц выполнить план по пошиву с минимальным количеством отходов.
Таблица 1.3
Характеристики вариантов раскроя отрезов ткани по 10 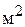
| Вариант раскроя | Количество деталей, шт./отрез | Отходы, 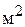 /отрез /отрез | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 0,5 | |||||||
| 0,35 | |||||||
| Комплектность, шт./изделие |
Решение
Переменные задачи
В данной задаче искомые величины явно не указаны, но сказано, что должен быть выполнен ежемесячный план по пошиву 90 изделий. Для пошива 90 изделий в месяц требуется раскроить строго определенное количество деталей. Крой производится из отрезов ткани по 10 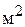 двумя различными способами, которые позволяют получить различное число деталей. Поскольку заранее неизвестно, сколько ткани будет раскраиваться первым способом и сколько – вторым, то в качестве искомых величин можно задать количество отрезов ткани по 10
двумя различными способами, которые позволяют получить различное число деталей. Поскольку заранее неизвестно, сколько ткани будет раскраиваться первым способом и сколько – вторым, то в качестве искомых величин можно задать количество отрезов ткани по 10 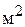 , раскроенных каждым из способов:
, раскроенных каждым из способов:
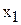 – количество отрезов ткани по 10
– количество отрезов ткани по 10 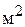 , раскроенных первым способом в течение месяца, [отрез./мес.];
, раскроенных первым способом в течение месяца, [отрез./мес.];
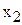 – количество отрезов ткани по 10
– количество отрезов ткани по 10 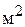 , раскроенных вторым способом в течение месяца, [отрез./мес.].
, раскроенных вторым способом в течение месяца, [отрез./мес.].
Целевая функция
Целью решения задачи является выполнение плана при минимальном количестве отходов. Поскольку количество изделий строго запланировано (90 шт./мес.), то этот параметр не описывает ЦФ, а относится к ограничению, невыполнение которого означает, что задача не решена. А критерием эффективности выполнения плана служит параметр "количество отходов", который необходимо свести к минимуму. Поскольку при раскрое одного отреза (10 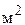 ) ткани по 1-му варианту получается 0,5
) ткани по 1-му варианту получается 0,5 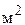 отходов, а по 2-му варианту – 0,35
отходов, а по 2-му варианту – 0,35 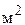 (см. табл.1.3), то общее количество отходов при крое (ЦФ) имеет вид
(см. табл.1.3), то общее количество отходов при крое (ЦФ) имеет вид
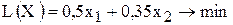 ,
,
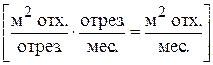 .
.
Ограничения
Количество раскроев ткани различными способами ограничивается следующими условиями:
· должен быть выполнен план по пошиву изделий, другими словами, общее количество выкроенных деталей должно быть таким, чтобы из него можно было пошить 90 изделий в месяц, а именно: деталей 1-го вида должно быть как минимум 90 и деталей остальных видов – как минимум по 180 (см. комплектность в табл.1.3).
· расход ткани не должен превышать месячного запаса его на складе;
· количество отрезов раскроенной ткани не может быть отрицательным.
Ограничения по плану пошива пальто имеют следующую содержательную форму записи
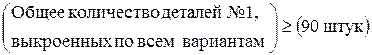 ;
;
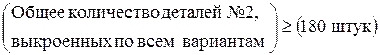 ;
;
…
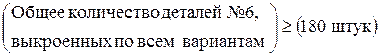 .
.
Математически эти ограничения записываются в виде
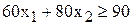 ;
;
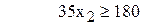 ;
;
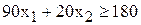 ;
;
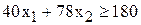 ;
;
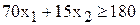 ;
;
 ;
;
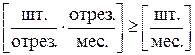 .
.
Ограничение по расходу тканиимеет следующие формы записи:
Содержательную
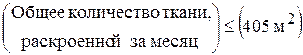
и математическую
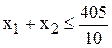 ,
,
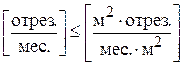 .
.
Неотрицательность количества раскроенных отрезов задается в виде
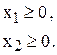
Таким образом, математическая модель задачи №1.03 имеет вид
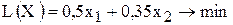 [м2 отх./мес.],
[м2 отх./мес.],
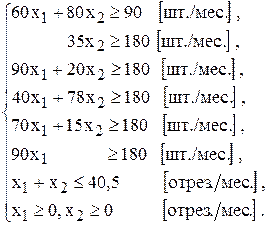
Вопрос 1.1*. При составлении математической модели задачи на следующий месяц следует учесть, что с прошлого месяца, возможно, остались выкроенные, но неиспользованные детали. Как это сделать?
Варианты задач для самостоятельного решения
Задача №1.1
Фирма выпускает три вида изделий. В процессе производства используются три технологические операции. На рис.1.1 показана технологическая схема производства изделий
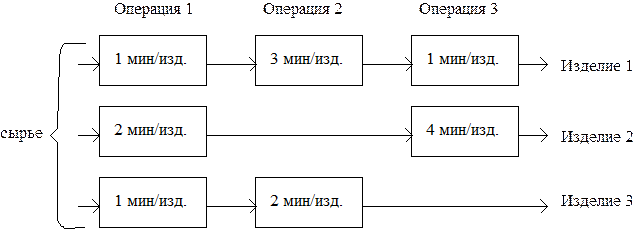
Рис.1.1. Технологическая схема производства
Фонд рабочего времени ограничен следующими предельными значениями: для первой операции – 430 мин; для второй операции – 460 мин; для третьей операции – 420 мин. Изучение рынка сбыта показало, что ожидаемая прибыль от продажи одного изделия видов 1, 2 и 3 составляет 3, 2 и 5 рублей соответственно.
Постройте математическую модель, позволяющую найти наиболее выгодный суточный объем производства каждого вида продукции?
Задача №1.2
При изготовлении изделий 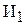 и
и 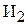 используются сталь и цветные металлы, а также токарные и фрезерные станки. По технологическим нормам на производство единицы изделия
используются сталь и цветные металлы, а также токарные и фрезерные станки. По технологическим нормам на производство единицы изделия 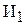 требуется 300 и 200 станко-часов соответственно токарного и фрезерного оборудования, а также 10 и 20 кг соответственно стали и цветных металлов. Для производства единицы изделия
требуется 300 и 200 станко-часов соответственно токарного и фрезерного оборудования, а также 10 и 20 кг соответственно стали и цветных металлов. Для производства единицы изделия 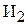 требуется 400, 100, 70 и 50 соответствующих единиц тех же ресурсов.
требуется 400, 100, 70 и 50 соответствующих единиц тех же ресурсов.
Цех располагает 12400 и 6800 станко-часами соответственно токарного и фрезерного оборудования и 640 и 840 кг соответственно стали и цветных металлов. Прибыль от реализации единицы изделия 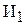 составляет 6 руб. и от единицы изделия
составляет 6 руб. и от единицы изделия 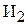 – 16 руб.
– 16 руб.
Постройте математическую модель задачи, используя в качестве показателя эффективности прибыль и учитывая, что время работы фрезерных станков должно быть использовано полностью.
Задача №1.3
Для сохранения нормальной жизнедеятельности человек должен в сутки потреблять белков не менее 120 условных единиц (усл. ед.), жиров – не менее 70 и витаминов – не менее 10 усл. ед. Содержание их в каждой единице продуктов 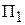 и
и 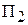 равно соответственно (0,2; 0,075; 0) и (0,1; 0,1; 0,1) усл. ед. Стоимость 1 ед. продукта
равно соответственно (0,2; 0,075; 0) и (0,1; 0,1; 0,1) усл. ед. Стоимость 1 ед. продукта 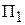 – 2 руб.,
– 2 руб., 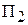 –3 руб.
–3 руб.
Постройте математическую модель задачи, позволяющую так организовать питание, чтобы его стоимость была минимальной, а организм получил необходимое количество питательных веществ.
Задача №1.4
В районе лесного массива имеются лесопильный завод и фанерная фабрика. Чтобы получить 2,5 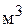 коммерчески реализуемых комплектов пиломатериалов, необходимо израсходовать 2,5
коммерчески реализуемых комплектов пиломатериалов, необходимо израсходовать 2,5 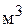 еловых и 7,5
еловых и 7,5 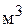 пихтовых лесоматериалов. Для приготовления листов фанеры по 100
пихтовых лесоматериалов. Для приготовления листов фанеры по 100 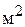 требуется 5
требуется 5 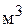 еловых и 10
еловых и 10 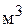 пихтовых лесоматериалов. Лесной массив содержит 80
пихтовых лесоматериалов. Лесной массив содержит 80 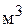 еловых и 180
еловых и 180 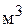 пихтовых лесоматериалов.
пихтовых лесоматериалов.
Согласно условиям поставок, в течение планируемого периода необходимо произвести по крайней мере 10 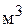 пиломатериалов и 1200
пиломатериалов и 1200 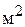 фанеры. Доход с 1
фанеры. Доход с 1 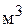 пиломатериалов составляет 160 руб., а со 100
пиломатериалов составляет 160 руб., а со 100 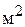 фанеры – 600 руб.
фанеры – 600 руб.
Постройте математическую модель для нахождения плана производства, максимизирующего доход.
Примечание 1.3. При построении модели следует учесть тот факт, что пиломатериалы могут быть реализованы только в виде неделимого комплекта размером 2,5 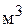 , а фанера – в виде неделимых листов по 100
, а фанера – в виде неделимых листов по 100 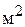 .
.
Задача №1.5
С вокзала можно отправлять ежедневно курьерские и скорые поезда. Вместимость вагонов и наличный парк вагонов на станции указаны в табл.1.4.
Таблица 1.4
