Красивые» задачи по чертежу
Задачи на построение чертежей, вызывают интерес именно условием (красивый чертеж). Поэтому учащиеся начинают фантазировать на данную тему, и у них получаются оригинальные чертежи.
Задача
Зигзаг разделил правильный девятиугольник на треугольники, как показано на рисунке. Какая часть площади больше: закрашенная или незакрашенная?
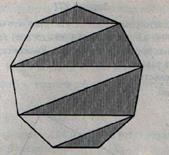
Решение. Проведем в девятиугольнике еще несколько диагоналей.
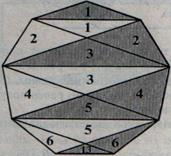
Девятиугольник разбился на 13 треугольников. На рисунке образовалось много параллелограммов и трапеций с диагоналями. Расставим номера треугольников, причем одинаковым номером отметим равные треугольники разных цветов. 12 из них разбились на пары, а тринадцатому, который оказался закрашенным, пары не хватило. Значит, закрашенная часть площади девятиугольника больше его незакрашенной части.
Ответ: закрашенная.
Красивые» задачи по решению
Нестандартность решения может проявляться и в методах решения. Особый интерес в этом смысле представляют задачи, имеющие несколько различных методов решения, и многовариантные задачи, имеющие несколько ответов (причем желательно, чтобы факт наличия нескольких ответов не был явно указан в формулировки условия).
Задача
Дан острый угол А, вершина которого недоступна (находится за пределами чертежа). Постройте биссектрису данного угла.
Эту задачу можно решить, как минимум, тремя способами, каждый из которых по-своему красив.
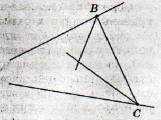
Способ 1 опирается на тот факт, что три биссектрисы треугольника пересекаются в одной точке. Взяв две произвольные точки В и С на сторонах данного угла, получим треугольник АВС (с одной недоступной вершиной), две биссектрисы которого можно построить. Точка пересечения этих биссектрис лежит на искомой биссектрисе. Аналогично можно найти и вторую точку.
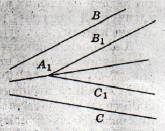
Способ 2 использует свойство углов с соответственно параллельными сторонами: проведя на равных расстояниях от сторон данного угла прямые А1В1и А1С1, параллельные соответственно сторонам АВ и АС, так чтобы точка их пересечения лежала внутри угла, получим угол В1А1С1, равный данному. Очевидно, что биссектриса В1А1С1 лежит на искомой биссектрисе угла ВАС.
Красивые» олимпиадные задачи
1) Олимпиадные задачи всегда пользовались успехом у учеников 5-11 классов,
приведу пример «красивой» олимпиадной задачи:
Задача
Дана белая доска размером 100*100 клеток. Двое по очереди красят ее клетки в черный цвет, причем первый всегда закрашивает квадрат 2*2, а второй—три клетки, образующие «уголок». Уже покрашенную клетку второй раз красить нельзя. Проигрывает тот, кто не может сделать очередной ход. Кто выигрывает при правильной игре: первый или второй?
Ответ: второй
 |
Рис.10
Решение. В одном из углов доски второй игрок своим первым ходом закрашивает три клетки в прямоугольнике 2x3, а три оставшиеся клетки из этого прямоугольника объявляет резервом (рис. 10). В дальнейшем второй игрок делает все возможные ходы, не затрагивая резерва. Если такой ход становится невозможным, то закрашиваются клетки резерва. Ясно, что ответного хода у первого игрока нет.
