Скалярное произведение векторов. Определение. Вычисление. Свойства.

Скалярное произведение векторов - число = произвед длин на косинус между ними.

Скалярное произ 2х векторов = модулю одного умноженного на проекцию другого на соноправленную с 1-ым вектором ось.

Свойства:

1.a*b=b*a

2. (C*a)*b=C*(a*b)

3. a(b+c)=a*c+b*c;

4.

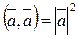
5. (a, b) = 0 =>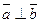

6. ij = jk = kj = 0.

Теорема 1: в пространстве R³ в ортонормированном базисе :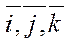

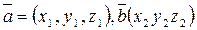
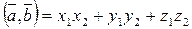
Следствие из Т1: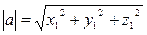

Для вектора :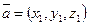

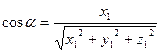
Механический смысл скалярного произведения:

Пусть 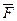- сила, которая перемещает тело в направлении вектора S ( на длину ) =>

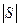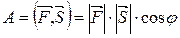
13. векторное произведение векторов. Определение. Вычисление. Свойства.

Три некомпланарных вектора a, b, с взяты в указанном порядке и образуют правую тройку, если с конца 3-его вектора с кратчайший поворот от 1-ого a ко 2-ому b видим совершающийся против часовой стрелки, и левую – если по часовой.

Векторное произведение вектора a на b - это c, который:

1)с перпендикулярно a и b;

2)имеет длину, численно равную площади параллельного, параллелограмма на векторах |c|=|a|*|b|*sinσ; 3) векторы a, b, с образ правую тройку.

Замечание: Из определения вытекает след соотношения между ортами ijk:

1. i*j=k;

2. j*k=i;

3. k*i=j;

Свойства:

1)векторное произ при перестановке множителей меняет знак. ( )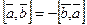

2)два ненулевых вектора коллинеарны, когда их векторное произв =0.

Пункты: 1)условие коллиниарности: a//b => a*b=0;

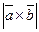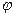2)нахождение S параллелограмма и S треуг. Sпар= sin . Sтр=0,5*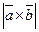

3)определение момента силы. |M|=|F|*|S|.

Теорема:

,

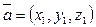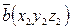
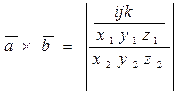
Смешанное произведение векторов. Определение. Вычисление. Свойства.

Смешанное произведение 3х векторов равно объёму параллелепипеда, построенного на этих векторах, взятого со знаком + (-), если эти векторы образуют правую (левую) тройку.

Свойства:

1)смешанное произв не меняется при циклической перестановке его множителей.

( .

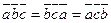2)смешанное произв меняет знак при перемене мест любых букв любых сомножителей

3)смешанное произ ненулевых векторов =0 тога, когда они компланарны.

Смешанное произ векторов = определителю 3-его порядка, составленного из координат перемноженных векторов.

Приложение. 1)определение взаимных ориентаций векторов в пространстве: если 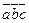>0 ( 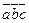<0), то правая (левая) тройка векторов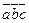

2)комплонарность векторов: 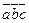компланарны, когда их произв =0.

3)Геометрический смысл: Vпараллелепипеда= 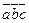. Vтр=1/6( ).

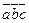Вычисление: ,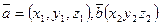

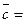
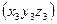
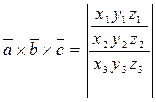
Прямая на плоскости.

Простейшей из линий является прямая. Разным способам задания прямой соответствует в прямоугольной система координат разные виды ее уравнений.

1. Уравнение прямой с угловым коэффициентом:

Пусть: tg 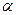=k, 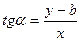, тогда: y = kx + b.

Число tg 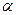=k называется угловым коэффициентом прямой, а уравнение – уравнением прямой с угловым коэффициентом.