Розв’язання. , складаємо

Вища математика * ТАВРІЙСЬКИЙ УНІВЕРСИТЕТ

МЕТОДИЧНІ ВКАЗІВКИ

Для індивідуальної роботи студентів очної форми навчання

З вищої математики

ФАКУЛЬТЕТ ІКТ

спеціальність «Машинобудування»

«Ряди»

Частина 1

Мелітополь

Розробила: ст. викл. Богаєвська Н.В.

Методичні вказівки розглянуті й схвалені на засіданні кафедри

протокол № ­­­­­­­­­­­­­­­­­­­­­­­­­ 10 від 12.05. 2009 р.

Рецензент: Омеляненко В.О.

Рекомендовані до видання методичною Радою факультету ІКТ

протокол №­­­­­­­­­­­­­­­­­­­­­­­­­ ______ від «______»______ 200 р.

І ЧИСЛОВІ РЯДИ

Основні поняття та означення

Розглянемо нескінченну послідовність чисел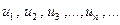

Означення 1. Вираз вигляду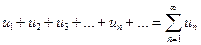

називається числовим рядом.

Приклади: а)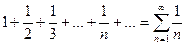

б)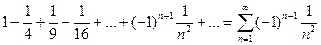

Означення 2. Числа 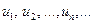називаються членами ряду, а вираз

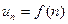- формулою загального члену ряду.

Означення 3. Сума n перших членів ряду називається n –ю частковою

сумою ряду.

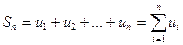
Означення 4. Якщо існує границя часткової суми 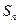при

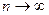
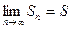, то ряд називається збіжним, а число 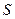- сумою ряду.

Приклад: Розглянемо геометричну прогресію

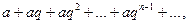де 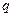- знаменник прогресії.

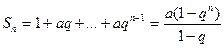
Розглянемо 3 випадки:

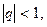
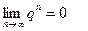а) тоді і

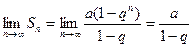
Отже, ряд є збіжним, його сума .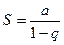

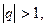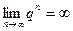б) тоді і 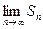- не існує.

Ряд розбігається.

в)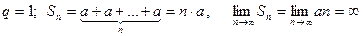

і ряд є розбіжним;

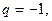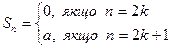тоді і

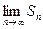- не існує, ряд розбігається.

Таким чином, геометрична прогресія 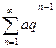збігається,

якщо 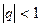, і розбігається, якщо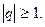

Означення 5. Різниця між сумою S збіжного ряду і його частковою сумою S_n називається залишком ряду.

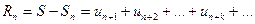
Залишок ряду також є числовим рядом.

Деякі властивості збіжних рядів

1. Якщо ряд 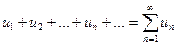збігається і має суму S , то ряд

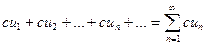також збігається і має суму .

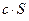2. Збіжні ряди можна почленно додавати або віднімати, тобто, якщо

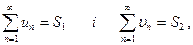то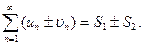

3. Відкидання будь-якого скінченого числа членів ряду не впливає на його збіжність або розбіжність, тобто, якщо ряд 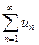є збіжним ( розбіжним), то його залишок 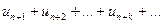також є збіжним ( розбіжним ).

Встановити збіжність ( розбіжність ) ряду шляхом визначення S_n і обчислення 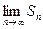можливо далеко не завжди через принципові труднощі

знаходження S_n . Простіше це можна зробити на основі ознак збіжності.

Необхідна ознака збіжності числового ряду

Розглянемо числовий ряд

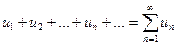( 1 )

Теорема. Якщо ряд ( 1 ) збіжний, то границя його загального члена при 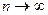дорівнює нулю, тобто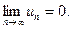

Умова 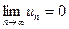є тільки необхідною, але недостатньою умовою збіжності

ряду.

Наприклад, для гармонічного ряду 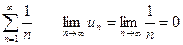, але можна

довести, що цей ряд є розбіжним.

Достатня умова розбіжності ряду

Якщо 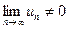ряд ( 1 ) є розбіжним.

Приклад. Дослідити ряд 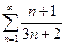на збіжність.

Розв’язання. Загальний член ряду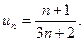

Оскільки 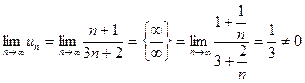, то ряд є розбіжним.

Достатні ознаки збіжності

Ознаки порівняння.

Нехай маємо два ряди:

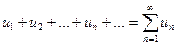( 1 )

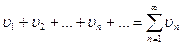( 2 )

1) Якщо ряд ( 2 ) збігається, а члени ряду ( 1 ) не перевищують відповідних членів ряду ( 2 ), тобто 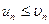то ряд ( 1 ) також збігається.

2) Якщо ряд ( 2 ) розбігається, а члени ряду ( 1 ) не менші за відповідні члени ряду ( 2 ), тобто 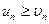, то ряд ( 1 ) також розбігається.

3) Якщо існує 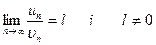, то ряди ( 1 ) і ( 2 ) є одночасно збіжними або розбіжними.

У якості рядів порівняння найчастіше беруть такі ряди:

а) Геометрична прогресія:

збігається, якщо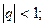

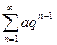
розбігається, якщо .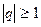

б) Узагальнений гармонічний ряд або ряд Діріхле:

збігається, якщо ;

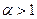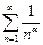
розбігається, якщо .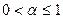

Приклади. Дослідити ряди на збіжність:

1)

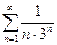
Розв’язання. Загальний член даного ряду

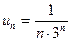
Ряд порівняння 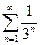- геометрична прогресія.

Оскільки і ряд 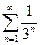є збіжним 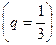, то даний ряд збігається.

2)

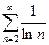
Розв’язання. 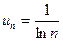. Ряд порівняння 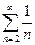- гармонічний ряд.

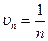, оскільки 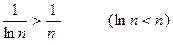і гармонічний ряд розбігається, то даний ряд є розбіжним.

3)

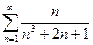
Розв’язання.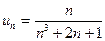

Ряд порівняння отримуємо, залишаючи в чисельнику і знаменнику загального члену лише найвищі степені n: .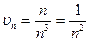

Отже, ряд порівняння 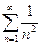- це є збіжний ряд Діріхле, оскільки .

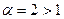Знайдемо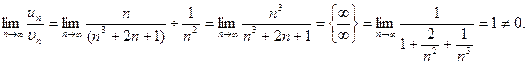

Оскільки ряд порівняння є збіжним, то даний ряд також збігається.

Завдання для самостійної роботи

І.Довести розбіжність рядів.

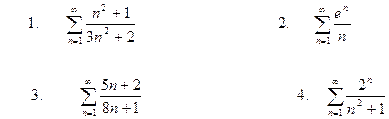
ІІ. Дослідити ряди на збіжність за допомогою ознак порівняння.

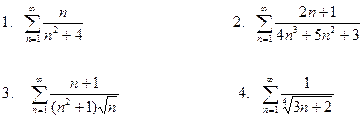
Ознака Даламбера

Розглянемо ряд з додатними членами:

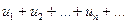( 1 )

Якщо існує границя 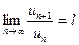, то:

1) ряд збігається, якщо l < 1;

2) ряд розбігається, якщо l >1;

3) якщо l = 1, то ознака не дає відповіді на питання про збіжність ряду (треба використати інші достатні ознаки збіжності).

Примітка. Якщо 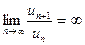, то ряд ( 1 ) є розбіжним.

Приклади. Дослідити ряди на збіжність:

1)

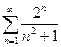
Розв’язання. , складаємо .

Знаходимо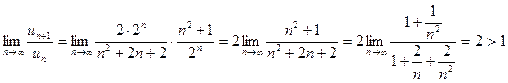

Отже, даний ряд є розбіжним.

2)

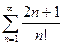
Розв’язання.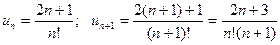

( за означенням ).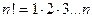

Знаходимо: ,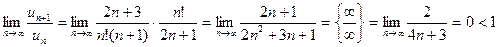

отже, ряд є збіжним.

( Невизначеність вигляду 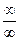було розкрито за допомогою правила Лопіталя).

3) .

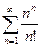Розв’язання.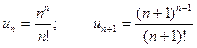

Знаходимо: ,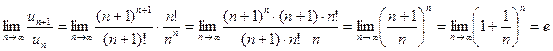

оскільки це є друга визначна границя.

, тому ряд є розбіжним.

Зауваження. Ознаку Даламбера доцільно застосовувати в тому випадку, коли загальний член ряду містить множники вигляду 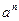або .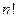

Завдання для самостійної роботи

За допомогою ознаки Даламбера дослідити ряди на збіжність.

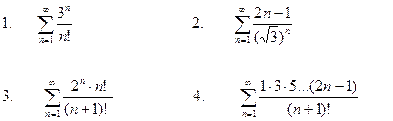
У прикладі 4: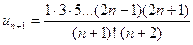

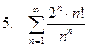
Радикальна ознака Коші