Уравнение в полных дифференциалах. Интегрирующий множитель

3.1 Уравнение в полных дифференциалах

Уравнение в полных дифференциалах имеет вид

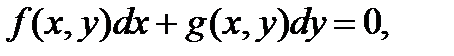где

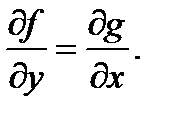
Левая часть этого уравнения представляет собой полный дифференциал некоторой функции двух переменных U (х, y).

Общий интеграл: U (х, y) = С, где функция U определяется из системы

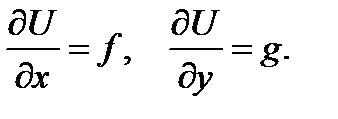
Интегрируя первое уравнение, имеем 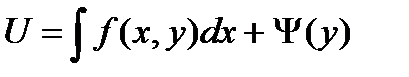(при интегрировании переменная у рассматривается как параметр). Подстановка этого выражения во второе уравнение позволяет найти функцию (а затем и функцию U ).

П р и м е р 7. Решить уравнение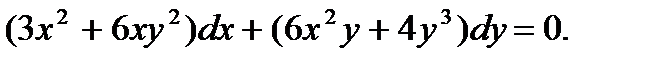

Здесь 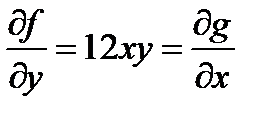, т.е. имеем уравнение в полных дифференциалах. Следовательно

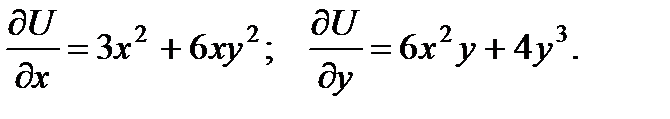
Первое уравнение интегрируем по х: 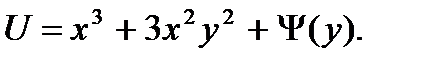Подставляя это во второе уравнение, получим 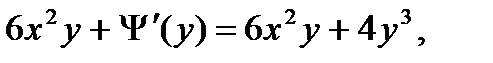откуда 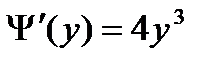или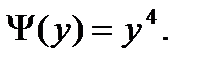

Окончательно 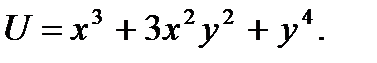Общий интеграл имеет вид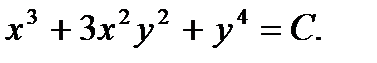

3.2 Интегрирующий множитель

Интегрирующим множителем для уравнения

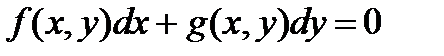
называется такая функция 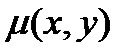не равная тождественно нулю, после умножения на которую левая часть этого уравнения становится полным дифференциалом, а само уравнение – уравнением в полных дифференциалах.

Интегрирующий множитель удовлетворяет уравнению с частными производными

первого порядка

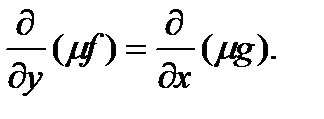
Но, если известно частное решение этого уравнения, то исходное уравнение интегрируемо в квадратурах.

П р и м е р 8. Проинтегрировать уравнение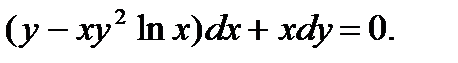

Уравнение для 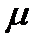имеет вид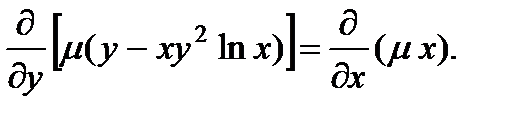

Попытаемся найти частное решение в виде 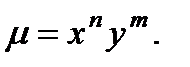Подстановка этой функции в последнее уравнение обращает его в тождество при m = n = -2 , следовательно 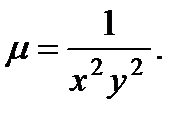Умножая исходное уравнение на эту функцию, превращаем его в уравнение в полных дифференциалах: 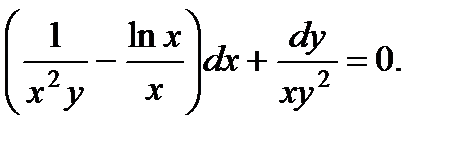Отсюда имеем два уравнения:

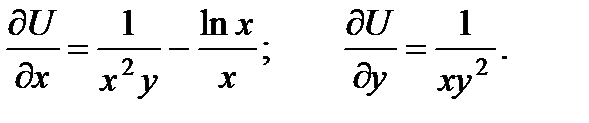
Здесь проще проинтегрировать второе уравнение по у : 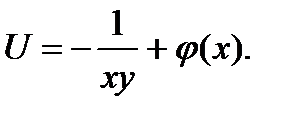Подставляя это в первое уравнение, получим 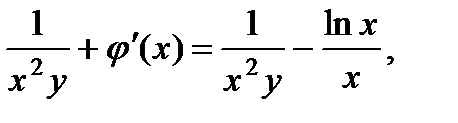откуда 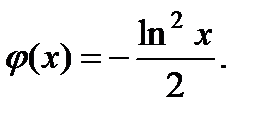Окончательно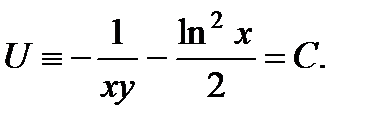

Уравнение Риккати

4.1 Общее уравнение Риккати. Простейшие случаи интегрирования

Общее уравнение Риккати имеет вид

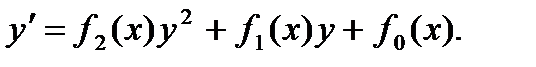(1)

При 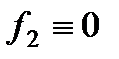оно вырождается в линейное уравнение (см. разд. 2.5), а при 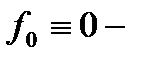в уравнение Бернулли (см. разд. 2.6 при а = 2). При произвольных функциях 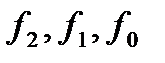уравнение Риккати в квадратурах не интегрируется.

Ниже указаны некоторые случаи, когда уравнение Риккати интегрируется в

квадратурах.

§ Функции 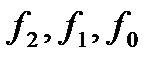пропорциональны:

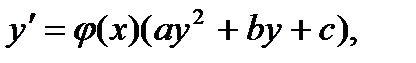
где a, b, c – константы. Это уравнение с разделяющимися переменными, см. разд. 2.1.

§ Уравнение Риккати

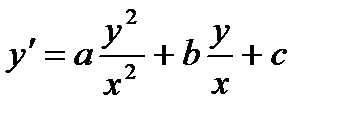
Является однородным, см. разд. 2.3.

§ Уравнение Риккати

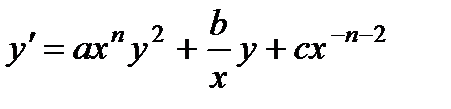
Является обобщенно-однородным, см. разд. 2.4 (при k = – n – 1). Замена 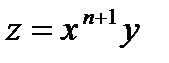приводит его к уравнению с разделяющимися переменными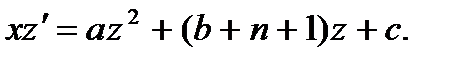

§ Уравнение Риккати

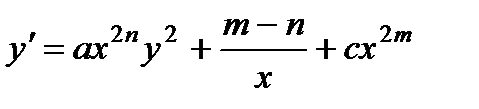
С помощью подстановки 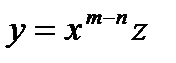приводится к уравнению с разделяющимися переменными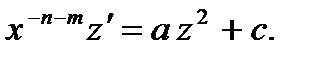

4.2 Использование частных решений для построения общего решения

§ Пусть известно частное решение Риккати 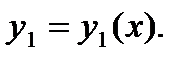Тогда подстановка

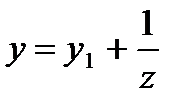приводит к линейному уравнению для z и, следовательно, уравнение Риккати решается в квадратурах.

П р и м е р 9. Проинтегрировать уравнение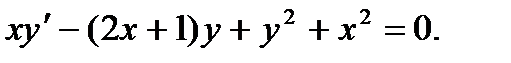

Поищем частное решение вида 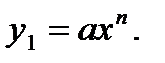Подставляя это в уравнение, находим 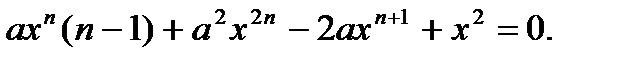Простейшим решением этого уравнения является n = 1, а = 1, т.е. у₁ = х. Подстановка 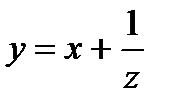приводит к линейному уравнению 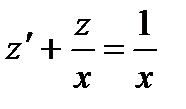, которое легко интегрируется: 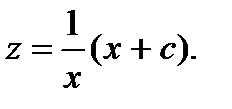Окончательно .

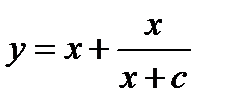§ Пусть 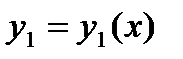и 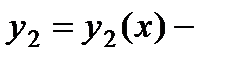два различных частных решения уравнения

(1). Тогда общее решение можно найти по формуле:

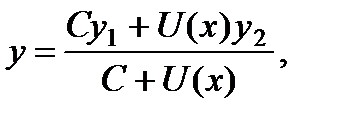где .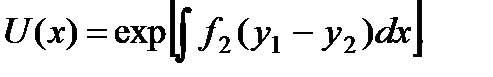

Частному решению у₁(х) соответствует значение 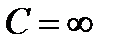, а решению у₂(х) – значение С = 0.

§ Пусть 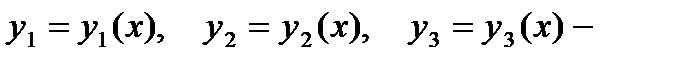три различных частных

решения уравнения (1). Тогда общее решение находится без квадратур:

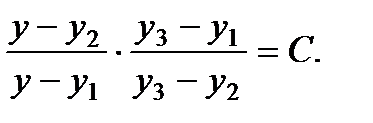
Это означает, что уравнение Риккати имеет фундаментальную систему решений.