Задания к контрольной работе

Контрольная работа должна быть выполнена в отдельной тетради в клетку в соответствии с вариантом, выбираемым по последней цифре номера зачетной книжки. При этом, если предпоследняя цифра учебного шифра нечетная (1, 3, 5, 7, 9), то номера заданий для соответствующего варианта даны в таблице 1. Если предпоследняя цифра четная или нуль (2, 4, 6, 8, 0), то номера задач даны в таблице 2. Каждая задача должна содержать условие, подробное решение и ответ.

Таблица 1

№ варианта	Номер задачи контрольной работы
№ 1	№ 2	№ 3	№ 4	№ 5	№6	№7	№8	№9

Таблица 2

№ варианта	Номер задачи контрольной работы
№ 1	№ 2	№ 3	№ 4	№ 5	№6	№7	№8	№9

Задача № 1

Вычислить определитель:

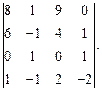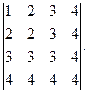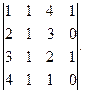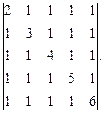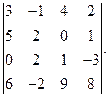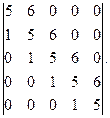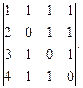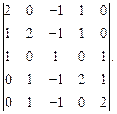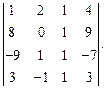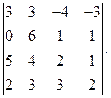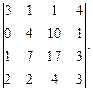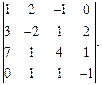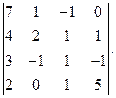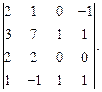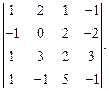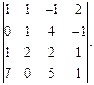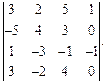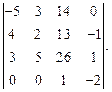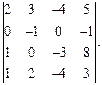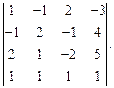Задача №2

1. Для матриц 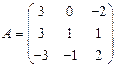и 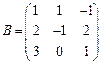вычислить матричный многочлен В² – ВА + 4В.
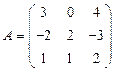2. Для матриц и 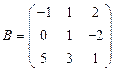вычислить матричный многочлен А² – ВА + 3А.
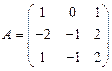3. Для матриц и 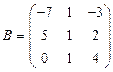вычислить матричный многочлен В² + ВА + 2А.
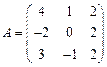4. Для матриц и 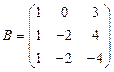вычислить матричный многочлен А² – 2ВА + А.
5. Для матриц 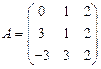и 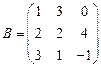вычислить матричный многочлен 2А² + ВА + 3А.
6. Для матриц 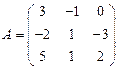и 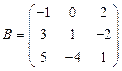вычислить матричный многочлен В² – ВА + 4А.
7. Для матриц 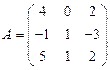и 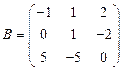вычислить матричный многочлен А² + ВА + 3В.
8. Для матриц 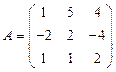и 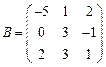вычислить матричный многочлен А² – ВА + 4В.
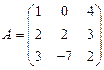9. Для матриц и 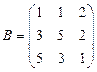вычислить матричный многочлен В² – ВА + 3А.
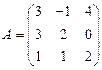10. Для матриц и 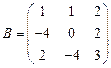вычислить матричный многочлен А² + 3ВА + 2В.
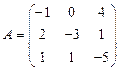11. Для матриц и 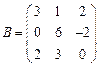вычислить матричный многочлен А² – ВА + 3А.
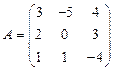12. Для матриц и 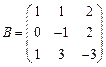вычислить матричный многочлен В² – ВА + 2А.
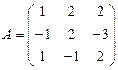13. Для матриц и 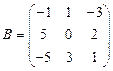вычислить матричный многочлен 3А² – ВА + В.
14. Для матриц 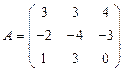и 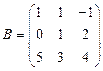вычислить матричный многочлен А² + 4ВА + В.
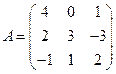15. Для матриц и 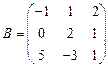вычислить матричный многочлен А² – ВА + 2В.
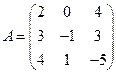16. Для матриц и 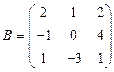вычислить матричный многочлен В² – ВА + 5А.
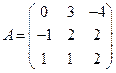17. Для матриц и 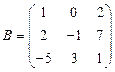вычислить матричный многочлен А² – ВА + 3А.
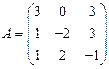18. Для матриц и 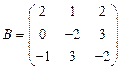вычислить матричный многочлен А² – ВА + 2В.
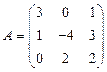19. Для матриц и 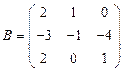вычислить матричный многочлен А² – 2ВА + 3В.
20. Для матриц 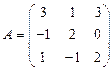и 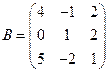вычислить матричный многочлен В² – ВА + 3А.

Задача № 3

Определить ранг матрицы.

41.		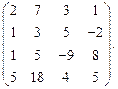42.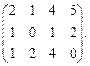
43.		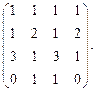44.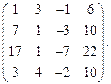
45.		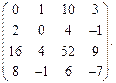46.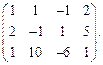
47.		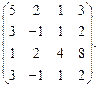48.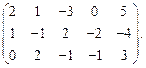
49.		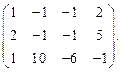50.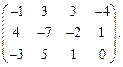
51.		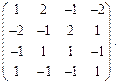52.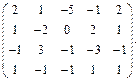
53.		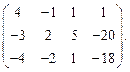54.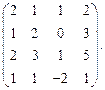
55.		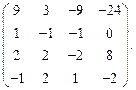56.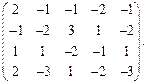
57.		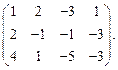58.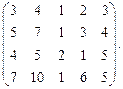
59.		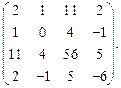60.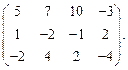

Задача № 4

Решить систему линейных уравнений тремя способами: 1) методом Гаусса; 2) формулами Крамера; 3) с помощью обратной матрицы.

61.		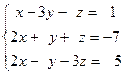62.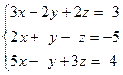
63.		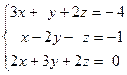64.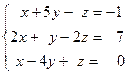
65.		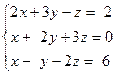66.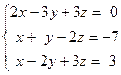
67.		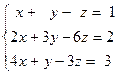68.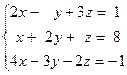
69.		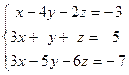70.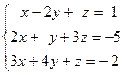
71.		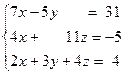72.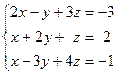
73.		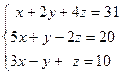74.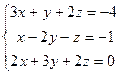
75.		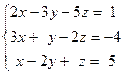76.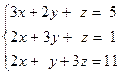
77.		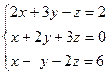78.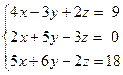
79.		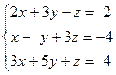80.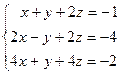

Задача № 5

Найти фундаментальную систему решений и общее решение системы однородных уравнений:

81.		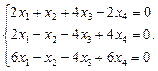82.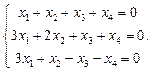
83.		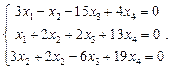84.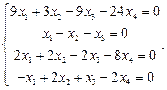
85.		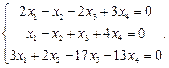86.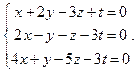
87.		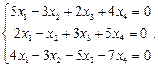88.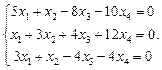
89.		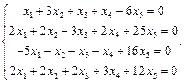90.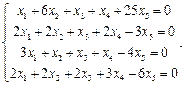
91.		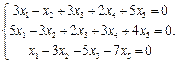92.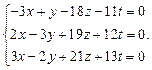
93.		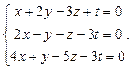94.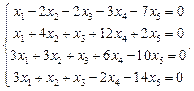
95.		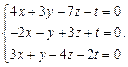96.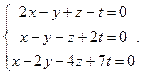
97.		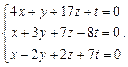98.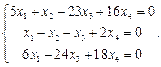
99.		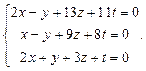100.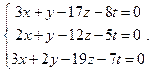

Задача №6

Даны вершины треугольника ABC. Найти: 1) уравнение прямой AB; 2) уравнение высоты CD и ее длину; 3) координаты векторов 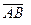и 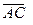; 4) угол A треугольника ABC.

101.		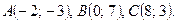102.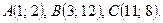
103.		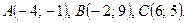104.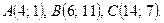
105.		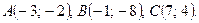106.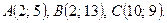
107.		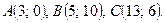108.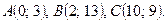
109.		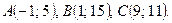110.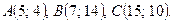
111.		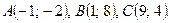112.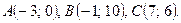
113.		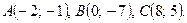114.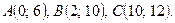
115.		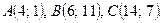116.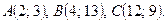
117.		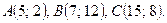118.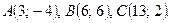
119.		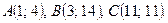120.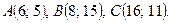

Задача № 7

Написать разложение вектора 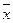по векторам 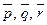или доказать, что это невозможно.

121.

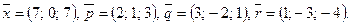
122.

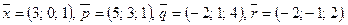
123.

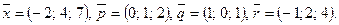
124.

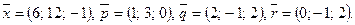
125.

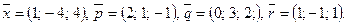
126.

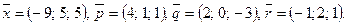
127.

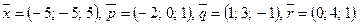
128.

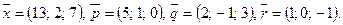
129.

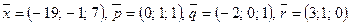
130.

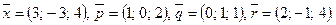
131.

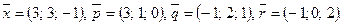
132.

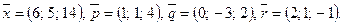
133.

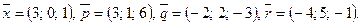
134.

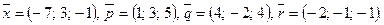
135.

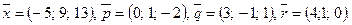
136.

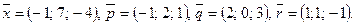
137.

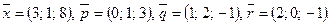
138.

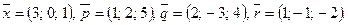
139.

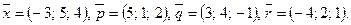
140.

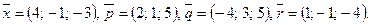
Задача № 8.

Найти собственные значения и собственные векторы матриц.

141.		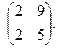142.		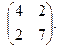143.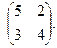
144.		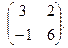145.		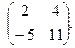146.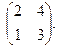
147.		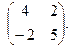148.		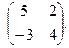149.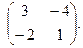
150.		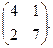151.		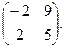152.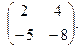
153.		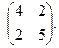154.		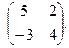155.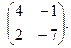
156.		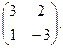157.		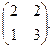158.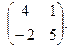
159.		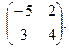160.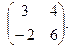

Задача № 9

Для приобретения оборудования для сортировки зерна фермер выделяет Aден.ед. Оборудование должно быть размещено на площади, не превышающей B кв. м. Фермер может заказать оборудование двух видов: менее мощные машины типа M1 стоимостью C ден.ед., требующие производственную площадь D кв. м и обеспечивающие производительность за смену 2т зерна, и более мощные машины типа B стоимостью E ден.ед, требующие производственную площадь F кв.м и обеспечивающие производительность 3т сортового зерна за смену.

Требуется составить оптимальный план приобретения оборудования, обеспечивающий максимальную общую производительность при условии, что фермер может приобрести не более Gмашин типа M2.

Составить математическую модель задачи и ее решить методом Гомори. Данные для решения задачи формируются по таблице 3.

Таблица 3. Значения коэффициентов.

№	A	B	C	D	E	F	G
8
8
8
8
8
8
8
9
9
9
9
9
0