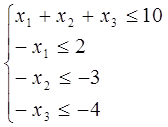Покажемо, що М-абелева група відносно операції додавання. 3 страница
д) З’ясуємо, чи є позитивно визначеною квадратична форма f. Квадратична форма f не буде позитивно визначеною, оскільки її другий головний мінор 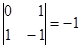 від’ємний.
від’ємний.
II. Записати квадратичну форму з матрицею А = 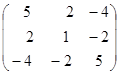
Розв’язання:
Матриці А відповідає наступна квадратична форма f:
f=5x12+x22+5x32+4x1x2-8x1x3-4x2x3.
III. Ортогональним перетворенням невідомих звести до канонічного виду квадратичну форму f=6x12+5x22+7x32-4x1x2+4x1x3.
Розв’язання. Матриця даної квадратичної форми f має вигляд:
А= 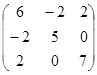 , її характеристична матриця А- λE =
, її характеристична матриця А- λE = 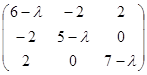 .
.
Розв’яжемо характеристичне рівняння:
|A- λE |=0; 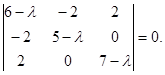
Власні числа цієї матриці λ1=3; λ2=6; λ3=9.
Знаходимо власні вектори, що відповідають цим власним значенням. Для цього розв’яжемо систему лінійних однорідних рівнянь:
(A-λiE)·X=0
Нехай λ1=3. Тоді відповідна система однорідних рівнянь
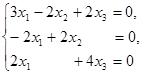
рангу 2 має фундаментальну систему розв’язків, що складається з одного вектора 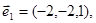 який є власним вектором, відповідним власному значенню λ1=3.
який є власним вектором, відповідним власному значенню λ1=3.
Нехай λ2=6; одержуємо систему однорідних рівнянь
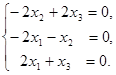
Розв’язавши її, знаходимо власний вектор 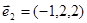 ,
,
Нехай λ3=9. Відповідна система лінійних однорідних рівнянь
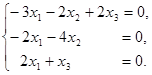
має фундаментальну систему розв’язків, що складається з вектора
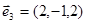 , який і буде власним вектором, відповідним власному значенню
, який і буде власним вектором, відповідним власному значенню  λ3=9.Одержана система векторів
λ3=9.Одержана система векторів 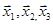 ортогональна, отже, лінійно незалежна і тому є одним з базисів трьохвимірного векторного простору. Нормуємо її, відповідні ортонормовані власні вектори
ортогональна, отже, лінійно незалежна і тому є одним з базисів трьохвимірного векторного простору. Нормуємо її, відповідні ортонормовані власні вектори
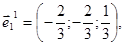
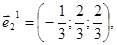
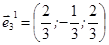 є ортонормованим базисом, в якому задана квадратична форма має канонічний вид:
є ортонормованим базисом, в якому задана квадратична форма має канонічний вид:
f1=3y12+6y22+9y32.
Відповідне лінійне перетворення координат має вигляд:
х1=- 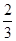 y1-
y1- 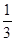 y2+
y2+ 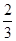 y3;
y3;
х2=- 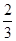 y1+
y1+ 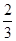 y2-
y2- 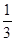 y3;
y3;
х3= 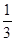 y1+
y1+ 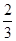 y2+
y2+ 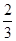 y3.
y3.
IV. Записати канонічне рівняння поверхні другого порядку, визначити її тип та знайти канонічну систему координат:
6х2+5y2+7z2-4xy+4xz-2x+6y-4z-1=0.
Розв’язання. Квадратична частина многочлена лівої частини рівняння має вигляд:
f=6х2+5y2+7z2-4xy+4xz, її матриця А= 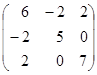 має власні числа
має власні числа 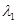 =3;
=3; 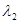 =6;
=6; 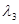 =9.
=9.
Відповідні ним ортонормовані власні вектори:
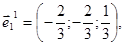
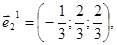
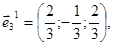
Виконаємо ортогональне перетворення невідомих за формулами:
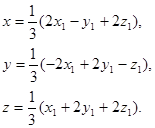
Одержуємо:
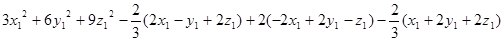 .
.
-1=0;
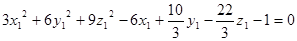 ;
;
Виконаємо перетворення зсуву за невідомими x1, y1, z1.
Друге перетворення координат має вигляд:
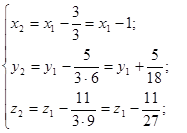
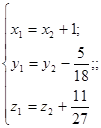
Одержуємо:
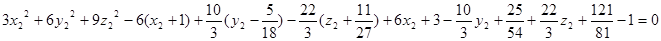
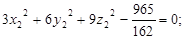 або
або 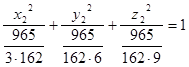 - канонічне рівняння еліпсоїду.
- канонічне рівняння еліпсоїду.
Остаточне перетворення координат:
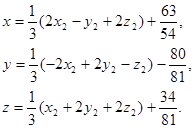
Канонічна система координат:
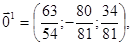
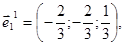
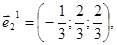
Контрольна робота №5.
І. Знайти область розв’язків наступних систем нерівностей:
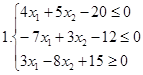 | |||||||||||||
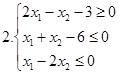 | |||||||||||||
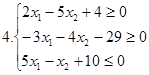 | |||||||||||||
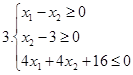 | |||||||||||||
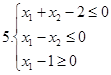 | 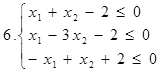 | ||||||||||||
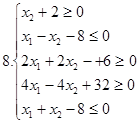 | |||||||||||||
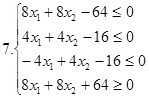 | |||||||||||||
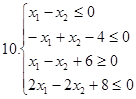 | |||||||||||||
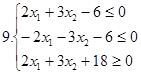 | |||||||||||||
ІІ. Дана система лінійних нерівностей та функція f:
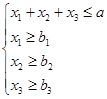 | |||
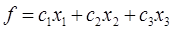 | |||
1. Дослідити систему лінійних нерівностей на сумісність.
а) за крітерієм Александрова,
б) за крітерієм Чернікова.
2. Розв’язати систему нерівностей
а) зведенням до системи рівнянь з 7 невідомими, 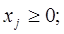
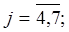
б) методом послідовного зменшення кількості невідомих.
3. Знайти мінімальні грані многогранника розв’язків заданої системи лінійних нерівностей.
4. Сформулювати стандартну та канонічну задачі для данної системи обмежень та цільової функції f.
5. Розв’язати симплекс - методом канонічну задачу, тобто знайти max (min) функції f на М.
Таблиця параметрів.
| Варіант | A | b1 | b2 | b3 | C1 | C2 | C3 | f |
| 1. | -1 | -1 | -3 | min | ||||
| 2. | -2 | -3 | -1 | max | ||||
| 3. | -2 | -2 | -5 | min | ||||
| 4. | -1 | -4 | -5 | max | ||||
| 5. | -1 | -2 | -3 | max | ||||
| 6. | -1 | -5 | -6 | min | ||||
| 7. | -1 | -5 | -3 | max | ||||
| 8. | -2 | -3 | -2 | min | ||||
| 9. | -4 | -2 | -4 | max | ||||
| 10. | -1 | -6 | -2 | min |
Зразки розв’язання задач контрольної роботи №5
І. Знайти область розв’язків системи лінійних нерівностей.
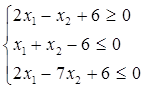
Розв’язання. Запишемо дану систему так:
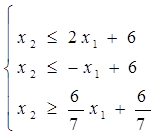
Перша нерівність цієї системи визначає півплощину, розміщену нижче від прямої 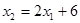 ; друга нерівність визначає півплощину, розміщену нижче від прямої
; друга нерівність визначає півплощину, розміщену нижче від прямої 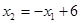 ; третя – півплошину, розміщену вище від прямої
; третя – півплошину, розміщену вище від прямої 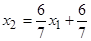 ;
;
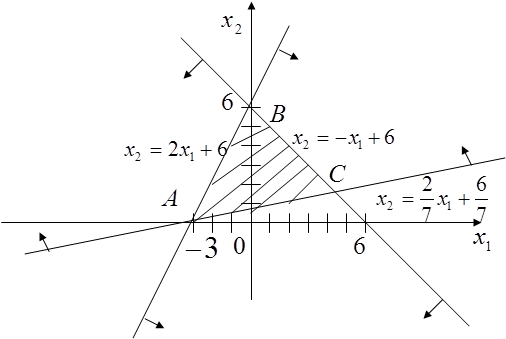 |
На малюнку напрям стрілок показує ту півплощину, яка визначаєтся відповідною нерівністю. Областю розв’язків данної системи нерівностей є трикутник АВС. Визначемо координати його вершин. Для цього знаходимо розв’язки таких систем рівнянь:
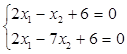
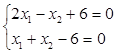
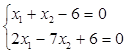
Розв‘язавши їх, маємо:
А(-3,0); В(0,6); С(4,2);
ІІ. Дана система лінійних нерівностей
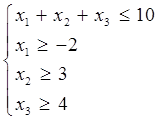
і функция 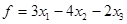 .
.
1.Дослідити систему лінійних нерівностей на сумісність
а)критерієм Александрова
б)критерієм Чернікова
2.Розв’язати систему нерівностей
а)зведенням до системи рівнянь з 7 навідомими, 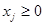 ,
, 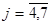 ;
;
б)методом послідовного зменшення кількості невідомих
3.Знайти мінімальні грані многогранника розв’язків.
4.Побудувати многогранники М і М+ (додатніх розв’язків систем)
5.Сформулювати загальну стандартну та канонічну задачі для заданої системи обмежень та цільвої функції f
6.Розв’язати симплекс-методом канонічну задачу.
Розв’язання
1.
а)запишемо систему нерівностей у вигляді
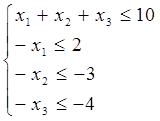
За критерієм Александрова система лінійних нерівностей несумісна тоді і тільки тоді, коли система лінійних рівнянь
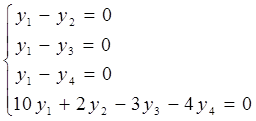
має невід’ємні розв’язки.
Розв’яжемо одержану систему лінійних рівнянь.


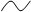
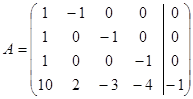
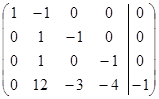
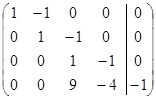
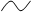
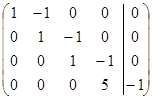
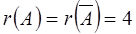
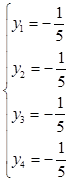 отже система лінійних рівнянь сумісна і має єдиний розв’язок.
отже система лінійних рівнянь сумісна і має єдиний розв’язок.
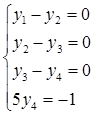
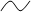 |
Розв’язком цієї системи є вектор 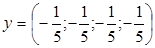 , тобто розв’язок від’ємний, і тому система лінійних нерівностей сумісна.
, тобто розв’язок від’ємний, і тому система лінійних нерівностей сумісна.
б)дослідемо систему лінійних нерівностей на сумісність за крітерієм Чернікова.
Обчислюємо ранг матриці системи лінійних нерівностей:

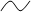
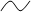

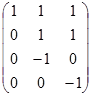

 r=3
r=3
Знаходимо відмінні від нуля мінори третього порядку:

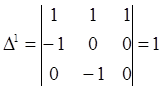 ;
; 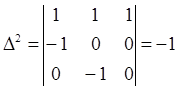 ;
; 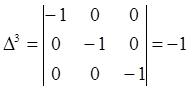
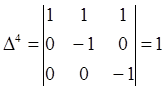
Супроводжуючі мінори:

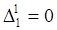 оскільки
оскільки 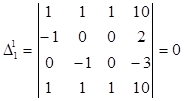 аналогічно
аналогічно
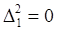
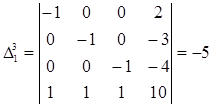
Відношення 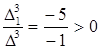
Отже, за крітерієм Чернікова система лінійних нерівностей сумісна.
2. а)системі лінійних нерівностей поставимо у відповідність систему лінійних рівнянь:
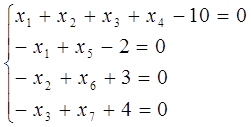
Розв’яжемо одержану систему лінійних рівнянь. Загальний розв’язок шукаємо у вигляді 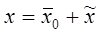 , де
, де 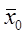 - частинний розв’язок,
- частинний розв’язок, 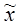 - загальний розв’язок відповідної однорідної системи лінійних рівнянь.
- загальний розв’язок відповідної однорідної системи лінійних рівнянь.

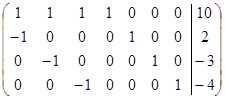
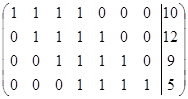
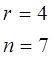

Система лінійних рівнянь сумісна і має безліч розв’язків (r<n).
Розв‘язуємо систему
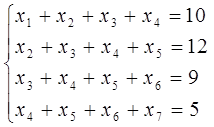
Знаходимо частинний розв’язок 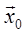 . Нехай
. Нехай 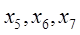 – вільні невідомі. Надамо
– вільні невідомі. Надамо 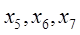 нульових значень, тобто
нульових значень, тобто 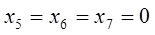
Тоді 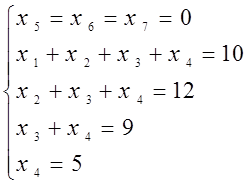
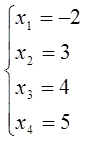
Отже, 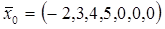 .
.
Відповідна однорідна система лінійних рівнянь має вид:
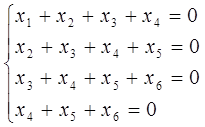
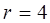
Фундаментальна система розв’язків цієї системи складаєтся з трьох векторів 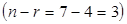 . У просторі R3 обираємо базис з векторів
. У просторі R3 обираємо базис з векторів
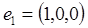

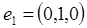
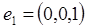
і вільним невідомим послідовно надаємо значень ціого базису.
Нехай 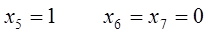
тоді
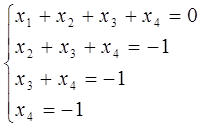
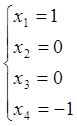
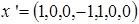
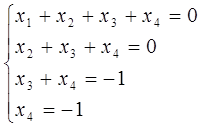
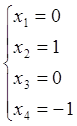
отже 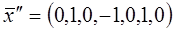
Нехай 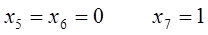 тоді
тоді
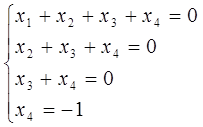
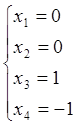 тоді
тоді
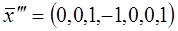
Загальний розвя’зок однорідної системи рівнянь є лінійна комбінація векторів фундаментальної системи розв’язків, тобто
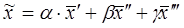
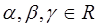
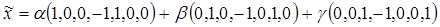 =
= 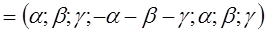
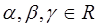
Загальний розв’язок системи неоднорідних рівнянь:
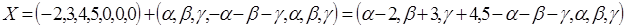
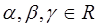
Отже, розв’язком системи лінійних нерівностей є вектор 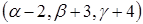
причому
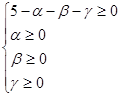 оскільки
оскільки 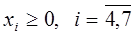
б) Розв’яжемо системи лінійних нерівностей методом послідовного зменшення кількості невідомих.
Запишемо систему у вигляді










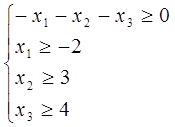
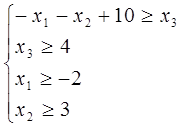
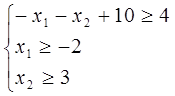
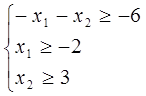
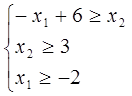
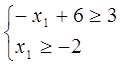
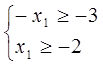
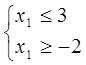
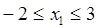
Нехай 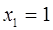 тоді
тоді 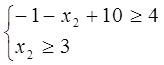
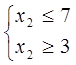
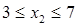
Нехай 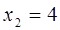 тоді
тоді 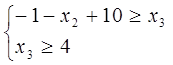
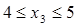 отже
отже 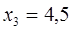
Звідси випливає, що вектор (1;4;4,5) є одним з розіязків системи лінійних нерівностей.
З загального розв’язку системи лінійних нерівностей 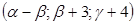 можна одержати розв’язок (1;4;4,5) якщо
можна одержати розв’язок (1;4;4,5) якщо 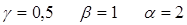
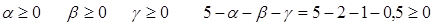
3.Знайдемо лінійні грані многогранника розв’язків системи лінійних нерівностей.
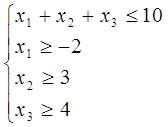
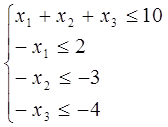
Обчислюємо ранг системи нерівностей



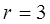
Виписуємо з даної системи рангу 3 усі лінійно незалежні підсистеми лінійних нерівностей 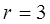 та замінюємо їх системами рівнянь, що одержуются в результаті заміни в системах нерівностей знаку нерівності на знак рівності.
та замінюємо їх системами рівнянь, що одержуются в результаті заміни в системах нерівностей знаку нерівності на знак рівності.
Одержуємо
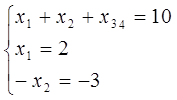
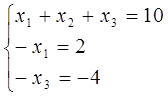
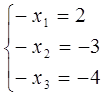
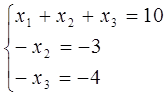
Оскільки ранг кожної з систем дорівнює кількості невідомих, то вони всі мають по єдиному розвязку.
Розв’яжемо ці системи. Одержуємо
(-2,8,4); (-2,3,4); (3,3,4) – розв’язки відповідних систем рангу r= 3.
Ці розв’язки задовольняють і системі лінійних нерівностей рангу r=3=n, тому є вершинами многогранника, тобто мінімальними гранями многогранника розв’язків.
4.Сформулюємо стандартну та канонічну задачі для данної системи обмежень та цільової функції f.
Стандартна задача:
Знайти max функції f=3x1-4x2-2x3 на множині невід’ємних розвязків системи нерівностей
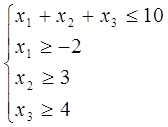 або
або