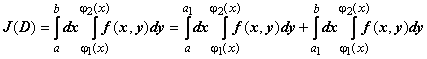Вычисление двойного интеграла. Двукратный интеграл
При вычислении двойного интеграла 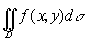 элемент площади
элемент площади 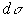 нам удобно представить в ином виде. Будем разбивать область интегрирования D в плоскости Oxy на частичные области посредством двух систем координатных линий: x=const, y=const. Этими линиями служат прямые, параллельные соответственно оси Oy и оси Ox, а частичными областями - прямоугольники со сторонами, параллельными осям координат. Ясно, что площадь каждой частичной области
нам удобно представить в ином виде. Будем разбивать область интегрирования D в плоскости Oxy на частичные области посредством двух систем координатных линий: x=const, y=const. Этими линиями служат прямые, параллельные соответственно оси Oy и оси Ox, а частичными областями - прямоугольники со сторонами, параллельными осям координат. Ясно, что площадь каждой частичной области 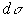 будет равна произведению соответствующих
будет равна произведению соответствующих 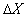 и
и 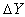 . Поэтому элемент площади
. Поэтому элемент площади 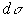 мы запишем в виде
мы запишем в виде 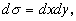 т.е. элемент площади в декартовых координатах является произведением дифференциалов независимых переменных. Мы имеем
т.е. элемент площади в декартовых координатах является произведением дифференциалов независимых переменных. Мы имеем
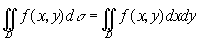 . (*)
. (*)
При вычислении двойного интеграла (*) мы будем опираться на тот факт, что он выражает объём V цилиндрического тела с основанием D, ограниченного поверхностью 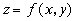 . Напомним, что мы уже занимались задачей об объёме тела, когда рассматривали применения определённого интеграла к задачам геометрии и получили формулу
. Напомним, что мы уже занимались задачей об объёме тела, когда рассматривали применения определённого интеграла к задачам геометрии и получили формулу
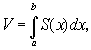 (**)
(**)
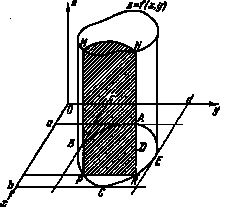
Рис.3
где S(х) - площадь поперечного сечения тела плоскостью, перпендикулярной к оси абсцисс, а 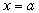 и
и 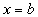 - уравнения плоскостей, ограничивающих тело. Применим теперь эту формулу к вычислению двойного интеграла
- уравнения плоскостей, ограничивающих тело. Применим теперь эту формулу к вычислению двойного интеграла
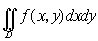
Предположим сначала, что область интегрирования D удовлетворяет следующему условию: любая прямая, параллельная оси Ox или Oy, пересекает границу области не более чем в двух точках. Соответствующее цилиндрическое тело изображено на рис.3
Область D заключим внутрь прямоугольника
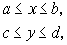
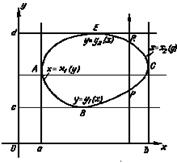
стороны которого касаются границы области в точках А, В, С, Е. Интервал [а, b] является ортогональной проекцией области D на ось Ох, а интервал [c, d] - ортогональной проекцией области D на ось Oy. На рис.5 область D показана в плоскости Оху.
Точками A и C граница разбивается на две линии: ABC и AEC, каждая из которых пересекается с любой прямой, параллельной оси Oy, в одной точке. Поэтому, их уравнения можно записать в форме, разрешенной относительно y:
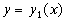 (ABC),
(ABC),
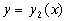 (AEC).
(AEC).
Аналогично точками В и Е граница разбивается на линии ВАЕ и ВСЕ, уравнения которых можно записать так:
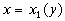 (BAE),
(BAE),
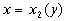 (BCE).
(BCE).
Двукратный интеграл
Двукратный (повторный) интеграл . Пусть D - область, простая в направлении оси Oy. Рассмотрим выражение 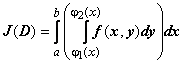 . Эта конструкция определяется через два обычных определённых интеграла. После интегрирования по у во внутреннем интеграле (переменная х при этом рассматривается как постоянная) и подстановки по у в пределах от
. Эта конструкция определяется через два обычных определённых интеграла. После интегрирования по у во внутреннем интеграле (переменная х при этом рассматривается как постоянная) и подстановки по у в пределах от 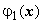 до
до 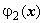 получается функция, зависящая только от х, которая интегрируется в пределах от a до b. В дальнейшем мы будем обычно записывать этот объект без внутренних скобок:
получается функция, зависящая только от х, которая интегрируется в пределах от a до b. В дальнейшем мы будем обычно записывать этот объект без внутренних скобок:
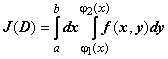 .
.
Можно показать, что двукратный интеграл обладает всеми свойствами двойного интеграла:
Свойства линейности и интегрирования неравенств следуют из этих свойств определённого интеграла; интеграл от единичной функции даёт площадь областиD: 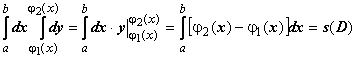 ;
;
теоремы об оценке и о среднем следуют из перечисленных свойств. Единственное свойство, с которым придётся повозиться - это свойство аддитивности. Мы докажем его в простой, но достаточной для нас форме: если область D разбита на две подобласти D1 и D2 прямой, параллельной одной из координатных осей, то двукратный интеграл по области D равен сумме интегралов по D1 и D2: J(D) = J(D1) + J(D2).
Первый случай: прямая x = a1 параллельна оси Oy. Тогда