Раздел: Аналитическая геометрия
Контроль самостоятельной работы студентов
ТЕСТЫ
Составитель: Сперанский Д.В., д.т.н., проф.
Раздел: Элементы векторного анализа
1.На плоскости заданы две точки: А=(5,10) и В =(7,12).Найдите координаты вектора 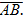
2. На плоскости заданы две точки А =(3,2) и В.Известны координаты вектора 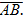 = (4,-1). Найдите координаты точки В.
= (4,-1). Найдите координаты точки В.
3. На плоскости заданы две точки В=(4,5) и А.Известны координаты вектора 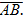 = (1,-6). Найдите координаты точки А.
= (1,-6). Найдите координаты точки А.
4. Найдите координаты точки С, делящей отрезок АВ в отношении АС:СВ=2:3, если координаты точек А=(-3,2), В=(2,4).
5. Найдите разложение вектора 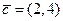 по базису
по базису 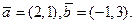
6. Найдите скалярное произведение 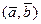 векторов
векторов 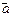 и
и 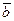 , если
, если 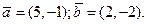
7. Заданы два вектора в пространстве: 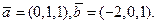 Найдите их сумму и разность.
Найдите их сумму и разность.
8. Найдите векторы, перпендикулярные вектору 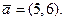
9. Используя свойства векторного произведения векторов, найдите координаты вектора, который перпендикулярен плоскости, проходящей через точки А =(1,2,-1), В=(3,2,0), С=(0,1,-1).
10. Используя свойства векторного произведения векторов, найдите площадь треугольника с вершинами А=(-1,0,2), В=(3,-1,0), С=(2,1,1).
11.Найдите смешанное произведение векторов 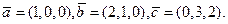
12. Используя смешанное произведение векторов, найдите объем параллелепипеда, построенного на векторах 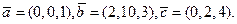
13. Найдите длину вектора 
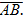 , если известны координаты точек А=(2,1,0), В=(7,5,0).
, если известны координаты точек А=(2,1,0), В=(7,5,0).
14. Используя свойство смешанного произведения векторов, найдите объем тетраэдра с вершинами А=(1,0,1), В=(2,-1,0),
С=(3,-1,2), D=(0,-1,1).
15. Используя свойство векторного произведения векторов, найдите площадь треугольника, построенного на векторах 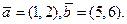
16. Найдите косинус угла между векторам 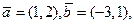 используя понятие скалярного произведения векторов.
используя понятие скалярного произведения векторов.
Раздел: Аналитическая геометрия
1.На плоскости заданы точки А = (-2,1) и В = (3,3). Найдите уравнение прямой, проходящей через них.
2. Даны точки А=(1,1) и В=(7,5). Найдите длину отрезка АВ.
3.Напишите уравнение окружности радиуса 4 с центром в точке (1,5).
4. Какая из прямых 1) y=3x+2; 2) 4x-2y+2=0; 3) 3x+y-2=0; 4) y= 6x+2 параллельна прямой y=2x+1?
5. Напишите каноническое уравнение эллипса, у которого большая полуось равна 3, малая полуось равна 2. Вычислите эксцентриситет e этого эллипса.
6. Напишите уравнение прямой, которая отсекает от начала координат отрезок длины 4 по оси OХ и отрезок длины 5 по оси OY.
7. Чему равен угловой коэффициент прямой 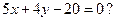
8. Какая из прямых 1) y=3x+2; 2) 4x-2y+2=0; 3) 3x+y-2=0; 4) y= 6x+2 перпендикулярна прямой 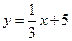 ?
?
9. Вычислите расстояние между точкой А =(1,2) и прямой 3х+4у+5=0.
10. Найдите уравнение плоскости, проходящей через точки А=(14,12,14), В=(13,14,15), С=(12,21,12).
11. Найдите эксцентриситет и директрисы эллипса 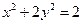 .
.
12. Составьте каноническое уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, что ее оси 2а=10 и 2в=8.
13. Выпишите уравнение параболы, расположенной в правой полуплоскости декартовой системы координат, у которой ось симметрии совпадает с осью OX и проходит через фокус параболы. Начало координат расположено посредине между фокусом и директрисой, перпендикулярной к оси OX. Известно, что расстояние между фокусом и директрисой равно 7. Выпишите также уравнение директрисы.
14.Напишите уравнение геометрического места точек, равноудаленных от точек А=(1,3,-2) и В= (-1,1,0).
15. Дана плоскость 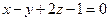 и прямая, проходящая через точки А = (2,3,0) и В = (0,1,1). Выпишите уравнение прямой, проходящей через эти точки, и вычислите косинус угла
и прямая, проходящая через точки А = (2,3,0) и В = (0,1,1). Выпишите уравнение прямой, проходящей через эти точки, и вычислите косинус угла 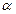 между прямой АВ и данной плоскостью.
между прямой АВ и данной плоскостью.
16. Дана сфера 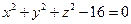 . Найдите центр О этой сферы и ее радиус R.
. Найдите центр О этой сферы и ее радиус R.
