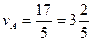Сведение матричной игры к задаче линейного программирования
Рассмотрим m 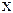 n игру с платежной матрицей А=(
n игру с платежной матрицей А=( 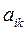 ).
).
Без ограничения общности будем считать, что все элементы матрицы А положительны (этого всегда можно добиться, пользуясь аффинным правилом, преобразующим заданную матрицу игры, но не изменяющим оптимальных смешанных стратегий игроков). Тогда искомая цена игры v— положительное число.
Интересы игрока А. Из теоремы о свойствах оптимальных смешанных стратегий игроков вытекает, что при любой чистой стратегии В 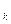 игрока В, k = 1, 2,.. . , n, оптимальная смешанная стратегия Р = {
игрока В, k = 1, 2,.. . , n, оптимальная смешанная стратегия Р = { 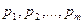 } игрока А обеспечивает его средний выигрыш, не меньший v. Иными словами, выполняются соотношения
} игрока А обеспечивает его средний выигрыш, не меньший v. Иными словами, выполняются соотношения 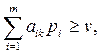 k=1,2,…,n,
k=1,2,…,n,
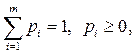 i=1,2,…,m,
i=1,2,…,m,
которые с учетом обозначений 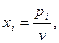 i=1,2,…,m, можно записать так
i=1,2,…,m, можно записать так
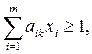 k=1,2,…,n,
k=1,2,…,n, 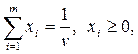 i=1,2,…,m.
i=1,2,…,m.
Поскольку игрок А стремится максимально увеличить свой гарантированный выигрыш, то задача отыскания решения матричной игры сводится к следующей задаче:
найти неотрицательные величины 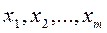 удовлетворяющие неравенству
удовлетворяющие неравенству 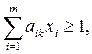 k=1,2,…,n и такие, что их сумма минимальна
k=1,2,…,n и такие, что их сумма минимальна
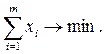
Интересы игрока В. Аналогичным образом заключаем, что оптимальная смешанная стратегия Q= { 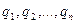 } игрока В при любой чистой стратегии А
} игрока В при любой чистой стратегии А 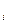 игрока А, i = 1,2,…,m обеспечивает его средний проитрыш, не больший v. Иными словами, выполняются соотношения
игрока А, i = 1,2,…,m обеспечивает его средний проитрыш, не больший v. Иными словами, выполняются соотношения
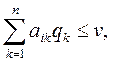 i=1,2,…,m,
i=1,2,…,m,
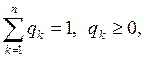 k=1,2,…,n, которые с учетом обозначений:
k=1,2,…,n, которые с учетом обозначений:
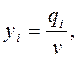 k=1,2,…,n можно записать так
k=1,2,…,n можно записать так 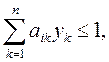 i=1,2,…,m,
i=1,2,…,m,
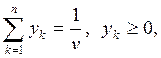 k=1,2,…,n.
k=1,2,…,n.
Поскольку игрок В стремится сделать свой гарантированный проигрыш минимально возможным, то задача отыскания решения матричной игры сводится к следующей задаче:
найти неотрицательные величины 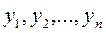 удовлетворяющие неравенству
удовлетворяющие неравенству 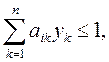 i=1,2,…,m и такие, что их сумма максимальна
i=1,2,…,m и такие, что их сумма максимальна
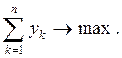
Тем самым, мы получаем следующий важный результат.
Теорема 3. Решение матричной игры с положительной платежной матрицей ( 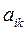 ) равносильно решению двойственных задач линейного программирования :
) равносильно решению двойственных задач линейного программирования :
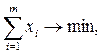
(А) 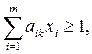 k=1,2,…,n,
k=1,2,…,n,
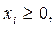 i = 1,2,…,m,
i = 1,2,…,m,
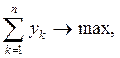
(B) 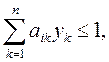 i=1,2,…,m,
i=1,2,…,m,
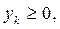 k = 1,2,…,n.
k = 1,2,…,n.
При этом цена игры v = 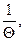 где Θ - величина, обратная общему значению оптимальных сумм, Θ =
где Θ - величина, обратная общему значению оптимальных сумм, Θ = 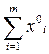 =
= 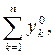 а оптимальные значения
а оптимальные значения 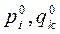 связаны с оптимальными
связаны с оптимальными 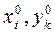 посредством равенств
посредством равенств
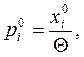 i=1,2,…,m,
i=1,2,…,m, 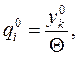 k = 1,2,…,n.
k = 1,2,…,n.
Алгоритм решения матричной игры.
1) Ко всем элементам исходной матрицы игры прибавляется одно и то же положительное число γ так, чтобы все элементы новой матрицы были строго положительны.
2) Решаются двойственные задачи линейного программирования (А) и (В) (например, симплекс-методом, или как-нибудь иначе). Находятся наборы 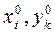 и число Θ.
и число Θ.
З) Строятся оптимальные смешанные стратегии игроков А и В соответственно 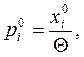
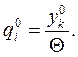
4) Вычисляется цена игры 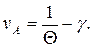
Пример 9. Рассмотрим 2 х 2 игру с матрицей 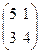 .
.
Соответствующие ей задачи линейного программирования имеют вид
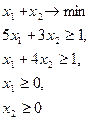
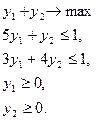
Решение.
1) Все элементы платежной матрицы положительны.
2) Строим решения обеих задач линейного программирования, пользуясь графическим методом. В результате получаем, что
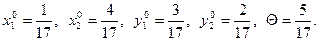
3) 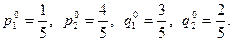
4)