Дифференцируемость ФМП. Полный дифференциал. Уравнения Касательной и нормали

нормаль

N

j N₀

касательная плоскость

Пусть N и N₀ – точки данной поверхности. Проведем прямую NN₀. Плоскость, которая проходит через точку N₀, называется касательной плоскостью к поверхности, если угол между секущей NN₀ и этой плоскостью стремится к нулю, когда стремится к нулю расстояние NN₀.

Определение. Нормальюк поверхности в точке N₀ называется прямая, проходящая через точку N₀ перпендикулярно касательной плоскости к этой поверхности.

В какой – либо точке поверхность имеет, либо только одну касательную плоскость, либо не имеет ее вовсе.

Если поверхность задана уравнением z = f(x, y), где f(x, y) – функция, дифференцируемая в точке М₀(х₀, у₀), касательная плоскость в точке N₀(x₀,y_0,(x₀,y₀)) существует и имеет уравнение:

.

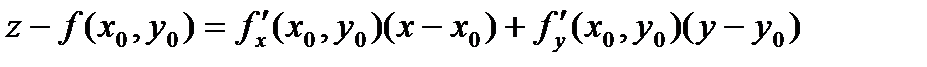Уравнение нормали к поверхности в этой точке: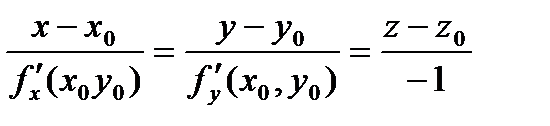

Пример. Найти уравнения касательной плоскости и нормали к поверхности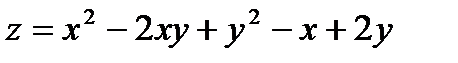

в точке М(1, 1, 1).

,

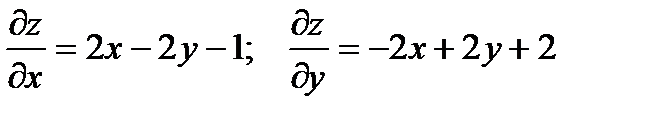Уравнение касательной плоскости: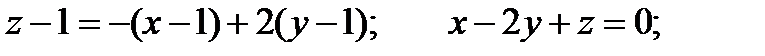

Уравнение нормали: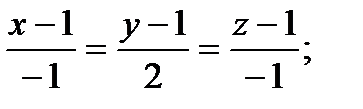

Градиент и полная производная ФМП. Производная по направлению. Частные производные высших порядков

Определение: Если в некоторой области D задана функция u = u(x, y, z) и некоторый вектор, проекции которого на координатные оси равны значениям функции u в соответствующей точке

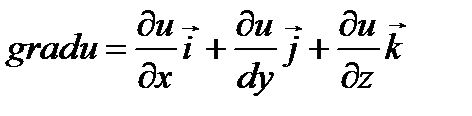, то этот вектор называется градиентомфункции u. При этом говорят, что в области D задано поле градиентов.Градиент ф-ии 1) – вектор, координатами к-го явл. част. производные по x,y,z.

Градиент направлен по нормали или линии уровня.

(grad(u)*ē)=|grad(u)|*| ē |*cosφ

ē=cosα*i+cosβ*j+cosγ*k

|∂F/∂x*cosα+∂F/∂y*cosβ+∂F/∂z*cosj|=|∂F/∂l|

|grad(u)|*cosφ=|∂F/∂l|

Рассмотрим функцию u(x, y, z) в точке М( x, y, z) и точке М₁( x + Dx, y + Dy, z + Dz).

Проведем через точки М и М₁ вектор . Углы наклона этого вектора к направлению координатных осей х, у, z обозначим соответственно a, b, g. Косинусы этих углов называются направляющими косинусамивектора .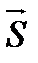

Расстояние между точками М и М₁ на векторе 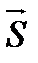обозначим DS.

z

M

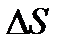
M₁

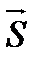
y

x

предположим, что функция u(x, y, z) непрерывна и имеет непрерывн частные пр по переменным х, у и z. Тогда:

Градиент и полная производная ФМП. Производная по направлению. Частные производные высших порядков 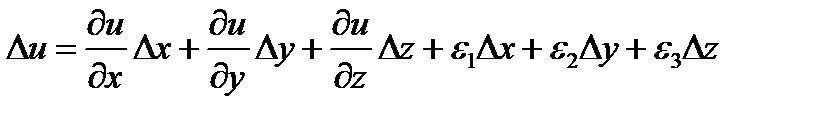, где e₁, e₂, e₃ – беск малые при .

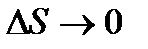Из геометрических соображений очевидно: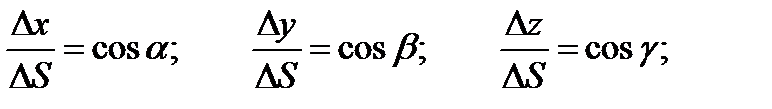

Таким образом, ;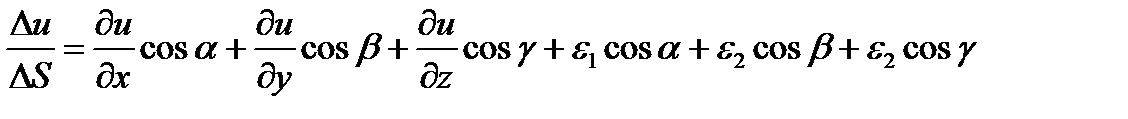

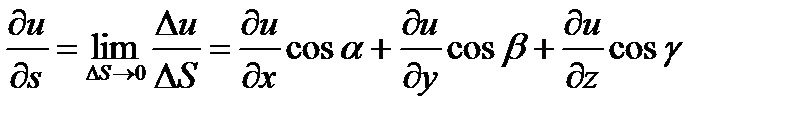
Заметим, что величина s является скалярной. Она лишь определяет направление вектора .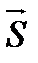

Определение: Предел 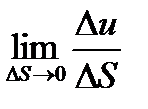называется производной функции u(x, y, z) по направлению вектора 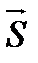в точке с координатами ( x, y, z).

23-24. Экстремум ФНП.

Определение. Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М₀(х₀, у₀) верно неравенство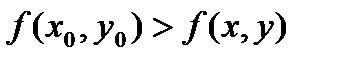

то точка М₀ называется точкой максимума.

Определение. Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М₀(х₀, у₀) верно неравенство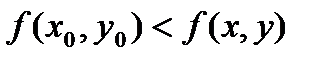

то точка М₀ называется точкой минимума.