Точечные и интервальные оценки случайных величин. Доверительный интервал. Доверительная вероятность. Аппроксимация экспериментальных зависимостей по методу наименьших квадратов

Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Возникает задача оценки параметров, которыми определяется это распределение.

Обычно в распоряжении исследователя имеются лишь данные выборки, полученные в результате n наблюдений (здесь и далее наблюдения предполагаются независимыми). Через эти данные и выражают оцениваемый параметр. Рассматривая значения количественного признака как независимые случайные величины, можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения - это значит найти функцию от наблюдаемых случайных величин, которая и дает приближенное значение оцениваемого параметра.

Итак, статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.

Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям: оценка должна быть несмещенной, эффективной и состоятельной.

Несмещенной называют статистическую оценку Q^*, математическое ожидание которой равно оцениваемому параметру Q при любом объеме выборки, т. е.

M(Q^*) = Q.

Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки п) имеет наименьшую возможную дисперсию.

При рассмотрении выборок большого объема (n велико!) к статистическим оценкам предъявляется требование состоятельности.

Состоятельной называют статистическую оценку, которая при п стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при п стремится к нулю, то такая оценка оказывается и состоятельной.

Рассмотрим точечные оценки параметров распределения, т.е. оценки, которые определяются одним числом Q^* =f( x₁, x₂,…,x_n), где x₁, x₂,…,x_n- выборка.

Пусть изучается генеральная совокупность относительно количественного признака Х.

Генеральной средней называют среднее арифметическое значений признака генеральной совокупности.

Если все значения признака различны, то

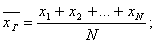
Если значения признака имеют частоты N₁, N₂, …, N_k, где N₁ +N₂+…+N_k= N, то

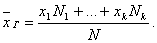
Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема n.

Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.

Если все значения признака выборки различны, то

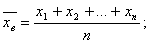
если же все значения имеют частоты n₁, n₂,…,n_k, то

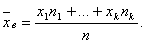
Выборочная средняя является несмещенной и состоятельной оценкой генеральной средней.

Замечание: Если выборка представлена интервальным вариационным рядом, то за x_i принимают середины частичных интервалов.

Для того чтобы охарактеризовать рассеяние значений количественного признака Х генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию.

Генеральной дисперсией D_г называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения .

Если все значения признака генеральной совокупности объема N различны, то

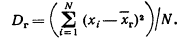
Если же значения признака имеют соответственно частоты N₁, N₂, …, N_k, где N₁ +N₂+…+N_k= N, то

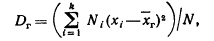
Кроме дисперсии для характеристики рассеяния зна­чений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой— средним квадратическим отклонением.

Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии:

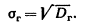
Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения , вводят сводную характеристику- выборочную дисперсию.

Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

Если все значения признака выборки различны, то

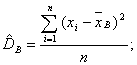
если же все значения имеют частоты n₁, n₂,…,n_k, то

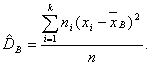
Для характеристики рассеивания значений признака выборки вокруг своего среднего значения пользуются сводной характеристикой - средним квадратическим отклонением.

Выборочным средним квадратическим отклоненим называют квадратный корень из выборочной дисперсии:

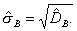
Вычисление дисперсии- выборочной или генеральной, можно упростить, используя формулу:

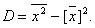
Замечание: если выборка представлена интервальным вариационным рядом, то за x_i принимают середины частичных интервалов.

Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно

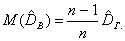
Для исправления выборочной дисперсии достаточно умножить ее на дробь

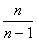получим исправленную дисперсию S². Исправленная дисперсия является несмещенной оценкой.

В качестве оценки генеральной дисперсии принимают исправленную дисперсию.

Для оценки среднего квадратического генеральной совокупности используют исправленное среднее квадратическое отклонение

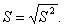
Замечание: формулы для вычисления выборочной дисперсии и исправленной дисперсии отличаются только знаменателями. При достаточно больших n выборочная и исправленная дисперсии мало отличаются, поэтому на практике исправленной дисперсией пользуются, если n<30.

Интервальной называют оценку, которая определяется двумя числами—концами интервала. Интервальные оценки позволяют установить точность и надежность оценок .

Пусть найденная по данным выборки статистическая характеристика Q* служит оценкой неизвестного пара­метра Q. Будем считать Q постоянным числом (Q может быть и случайной величиной). Ясно, что Q* тем точнее определяет параметр Q, чем меньше абсолютная величина разности |Q- Q*|. Другими словами, если >0 и |Q- Q*| < , то чем меньше  , тем оценка точнее.

Однако статистические методы не позволяют категорически утверждать, что оценка Q* удовлетворяет неравенству |Q- Q*| <; можно лишь говорить о вероятности , с которой это неравенство осуществляется.

Надежностью (доверительной вероятностью) оценки называют вероятность  , с которой осуществляется неравенство |Q—Q* | < .

Обычно надежность оценки задается наперед, причем в качестве g берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.

Пусть вероятность того, что, |Q- Q*| <d равна g: P(|Q- Q*| <d)= g. Заменив неравенство равносильным ему двойным неравенством получим: Р [Q* —< Q < Q* +] =  Это соотношение следует понимать так: вероятность того, что интервал Q* - d< Q < Q* +d заключает в себе (покрывает) неизвестный параметр Q, равна g.

Интервал (Q* -  Q* +) называется доверительным интервалом , который покрывает неизвестный параметр с надежностью .

Пусть количественный признак генеральной совокупности распределен нормально. Известно среднее квадратическое отклонение этого распределения -. Требуется оценить математическое ожидание а по выборочной средней. Найдем доверительный интервал, покрывающий а с надежностью . Выборочную среднюю будем рассматривать как случайную величину ( она изменяется от выборки к выборке), выборочные значения признака- как одинаково распределенные независимые СВ с математическим ожиданием каждой а и средним квадратическим отклонением . Примем без доказательства, что если величина Х распределена нормально, то и выборочная средняя тоже распределена нормально с параметрами

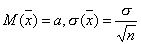.Потребуем, чтобы выполнялось равенство

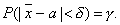Заменив Х и , получим

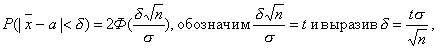
получим

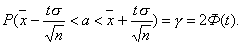
Задача решена. Число t находят по таблице функции Лапласа Ф(х).

Пример1. СВХ распределена нормально и s =3. Найти доверительный интервал для оценки математического ожидания по выборочным средним, если n = 36 и задана надежность  =0,95.

Из соотношения 2Ф(t)= 0,95 , откуда Ф(t) = 0,475 по таблице найдем t : t =1,96. Точность оценки

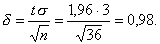
Доверительный интервал

.

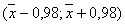Пример2. Найти минимальный объем выборки, который обеспечивает заданную точность d =0,3 и надежность g = 0,975, если СВХ распределена нормально и s =1,2.

Из равенства

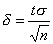
выразим n:

,

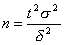подставим значения и получим минимльный объем выборки n ~ 81.

Т.к. мы не знакомы с законами распределения СВ, которые используются при выводе формулы, то примем ее без доказательства.

В качестве неизвестного параметра sиспользуют исправленную дисперсию s² . Заменяя gна s, t на величину tg. Значение этой величины зависит от надежности g и объема выборки n и определяется по " Таблице значений tg." Итак :

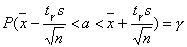
и доверительный интервал имеет вид

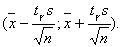
Пример1. Найти доверительный интервал для оценки математического ожидания с надежностью 0,95, если объем выборки n =16, среднее выборочное и исправленная дисперсия соответственно равны 20,2 и 0,8.

По таблице приложения найдем t_по заданной надежности  =0,95 и n= 16: t_ =2,13. Подставим в формулу s =0,8 и t_ =2,13 , вычислим границы доверительного интевала:

,

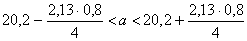откуда получим доверительный интервал (19,774; 20,626)

Смысл полученного результата: если взять 100 различных выборок, то в 95 из них математическое ожидание будет находится в пределах данного интервала, а в 5 из них- нет.

Пример2. Измеряют диаметры 25 корпусов электродвигателей. Получены выборочные характеристики

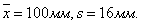
Необходимо найти вероятность (надежность) того, что

- является доверительным интервалом оценки математического ожидания при нормальном распределении.

Из условия задачи найдем точность d, составив и решив систему:

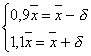
Откуда d =10. Из равенства

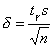
выразим

,

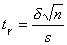откуда t_ =3,125. По таблице для найденного t_ и n= 25 находим  =0,99.