Положение равновесия и квазиупругая сила.

Рассмотрим одномерное движение тела под действием консервативной силы вдоль оси X. Для потенциальной энергии тела вблизи некоторой точкиx₀ можно записать выражение

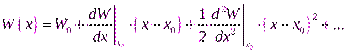
Потенциальная энергия и вектор консервативной силы связаны соотношением:

,

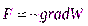откуда для проекции силы на ось Xполучаем: 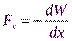, т.е.

.

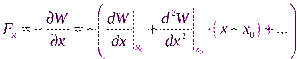Д 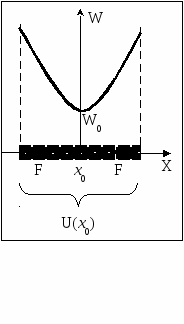алее будем предполагать, чтоточка x₀ является положением равновесия, поэтому должно выполняться условие 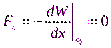, тогда для изменения потенциальной энергии вблизи точкиx₀имеем: 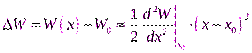и для проекции силы: .

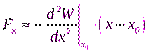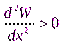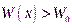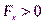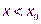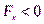Рассмотрим случай, когда в точке x₀наблюдается локальный минимум потенциальной энергии. Тогда и существует некоторая окрестность точкиU(x₀), для которой выполняется условие и при , при 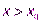, то есть в этой окрестности вектор силы, действующей на тело, будет направлен к точкеx₀. А это значит, чтопри малых смещениях тела из положения равновесия, сила будет стремиться вернуть тело обратно. Такое положение равновесия называется устойчивым.

Положение равновесия называется неустойчивым, если при малом отклонении от этого положения возникает сила, стремящаяся увести тело от положения равновесия. Очевидно, в этом случае в точкеx₀ наблюдается локальный максимум потенциальной энергии .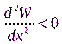

В случае, когда 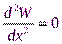требуется дополнительное исследование.

Итак, выражение для консервативной силы вблизи положения устойчивого равновесия можно записать в векторной форме: 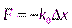,а величину потенциальной энергии 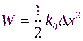+const, где 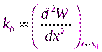. Такая форма записи для консервативной силы вблизи точки равновесия называетсяквазиупругой силой.

Запишем второй закон Ньютона для тела, движущегося под действием квазиупругой силы вблизи точки устойчивого положения равновесия:

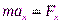, где .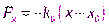

Введём ось Х так, чтобы 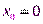, тогда уравнение движения примет вид: 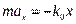. С учётом зависимости 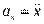это уравнение примет вид: 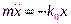или

,

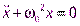где 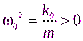. Этолинейное обыкновенное дифференциальное уравнение второго порядка.

Решением этого уравнения являются гармонические функции от времени t:

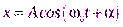или ,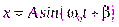

описывающие смещение тела от положения равновесия (точка ).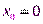

Замечание. Обе формы записи равноправны. Например, одна переходит в другую при .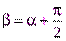

Так как гармонические функции синус и конус имеют период 2p, то параметры процесса будут повторяться через минимальный промежуток времени Т, называемыйпериодом:

.

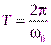Таким образом, уравнение

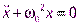
описывает колебательный процесс, параметры которого не изменяются с течением времени. Этот процесс принято называтьсвободными незатухающими колебаниями.

Учитывая, что величина 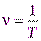называетсячастотой колебаний(единица измерения Гц - Герц), то величину 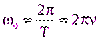называюткруговойилициклической частотой колебаний(единица измерения с^-1).

Величина А –амплитуда колебаний- это модуль максимального смещения.По определениюA > 0– всегда положительная величина. Аргумент гармонической функции 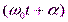называетсяфазой колебания, а величинаaназываетсяначальной фазой колебаний- это фаза колебаний в момент времениt = 0, который обычно называютначальным моментом времени.

В этом колебательном процессе с течением времени сохраняется величина механической энергии: 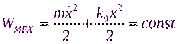. Действительно:

.
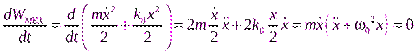