Квазиупругая сила. Математический и физический маятники. Циклическая частота гармонического осциллятора. Энергия колебаний.

КВАЗИУПРУГАЯ СИЛА - направленная к центру О сила. модуль к-рой пропорционален расстоянию r от центра О до точки приложения силы (F=-cr), где с - постоянный коэф., численно равный силе, действующей на единице расстояния. К. с. является силой центральной и потенциальной с силовой ф-цией U=-0,5cr². Примерами К. с. служат силы упругости, возникающие при малых деформациях упругих тел (отсюда и сам термин "К. с."). Приближённо К. с. можно также считать касательную составляющую силы тяжести, действующей на матем. маятник при малых его отклонениях от вертикали. Для материальной точки, находящейся под действием К. с., центр О является положением её устойчивого равновесия. Выведенная из этого положения точка будет в зависимости от нач. условий или совершать около О прямолинейные гармонич. колебания, или описывать эллипс (в частности, окружность).

Математический маятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомойнерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины l неподвижно подвешенного в однородном поле тяжести с ускорением свободного паденияg равен

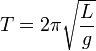
и не зависит^[1] от амплитуды и массы маятника.

Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.

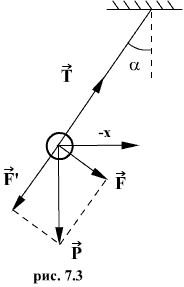
Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара. Если его отклонить на угол α (рис.7.3.) от вертикальной линии, то под влиянием силы F – одной из составляющих веса Р он будет совершать колебания. Другая составляющая 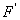, направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения 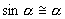и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна

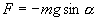
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α

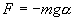
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения

Момент силы относительно точки О: 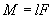, и момент инерции:
M = FL .
Момент инерции J в данном случае
Угловое ускорение:

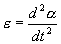
С учетом этих величин имеем:

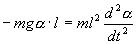
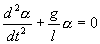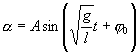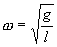Его решение где и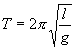

Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.

Физический маятник.

Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.

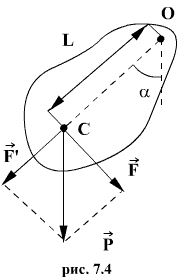
При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.

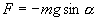
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α

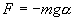
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения

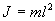. Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид: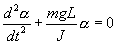

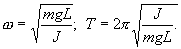
Решение этого уравнения

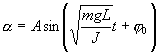
Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е. 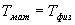или

.
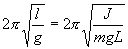Из этого соотношения определяем

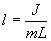
Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.

Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.

Осциллятор (от лат. oscillo — качаюсь) — система, совершающая колебания, то есть показатели которой периодически повторяются во времени.

Гармонический осциллятор (в классической механике) — это система, которая при смещении из положения равновесия испытывает действие возвращающей силы 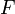, пропорциональной смещению 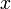(согласно закону Гука):

Упругие волны. Механизмы и условия возникновения упругих волн. Поперечные и продольные упругие волны, условия их возникновения. Формулы скорости упругих волн в различных средах. Длина волны. Циклическое волновое число. Уравнение плоской волны.

Упругие волны (звуковые волны) — волны, распространяющиеся в жидких, твёрдых и газообразных средах за счёт действия упругих сил.

В зависимости от частоты различают инфразвуковые, звуковые и ультразвуковые упругие волны.

В жидких и газообразных средах может распространяться только один тип упругих волн — продольные волны. В волне этого типа движение частиц осуществляется в направлении распространения волны.

В твёрдых телах существуют касательные напряжения, что приводит к существованию других типов волн, в которых движение частиц осуществляется по более сложным траекториям.

Упругие волны, распространяющиеся в земной коре, называют сейсмическими волнами.

Наиболее распространёнными типами упругих волн в твёрдых телах являются:

-продольные волны;

-поперечные волны, движение частиц перпендикулярно направлению распространения волны;

-поверхностные волны (например волны Рэлея, где движение частиц происходит по эллипсам);

-волны в тонких пластинах — волны Лэмба.

Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах. Величина 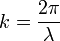, обратная длине волны, называется волновым числом и имеет смысл пространственной частоты.