Интегральные оценки качества переходных процессов

Интегральными оценками качества переходного процесса систем управления называют интегралы по времени от некоторых функций переходного процесса изменения ошибки регулирования.

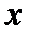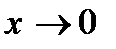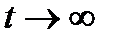Интегральными оценками качества называются такие, которые одним числом оценивают величины отклонений и время затухания переходного процесса. Будем отклонение в переходном процессе отсчитывать от нового установившегося состояния, так что при . Для монотонного процесса интегральной оценкой может служить площадь под кривой переходного процесса (рис. 15.10, а), т.е.

.

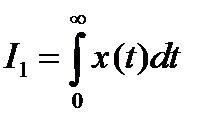Интеграл 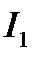имеет конечное значение для любого решения 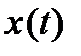линейного уравнения. Процесс будет считаться тем лучше, чем меньше число .

+

+

-

-

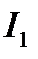x

t

x

t

а) б)

t

y

y(¥)

T

в)

Рис. 15.10 - Примеры монотонного переходного процесса (а), колебательной

величины ошибки САУ (б), колебательной регулируемой величины (в)

Интегральная оценка 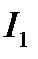применима только к системам.переходные процессы которых монотонны, что существенно ограничивает применимость этого критерия. Если переходный процесс колебательный (рис. 15.10, б), то значение 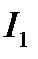не может служить мерой его качества, так как площади разного знака под кривой переходного процесса при вычислении интеграла будут вычитаться друг из друга. Поэтому по минимуму величины 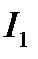наилучшим оказался бы процесс с незатухающими колебаниями (рис. 15.10, б- кривая 2), что недопустимо.

В связи с этим в общем случае принимают квадратичную интегральную оценку качества в виде

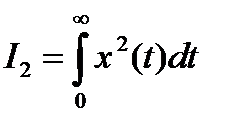. (15.12)

В учебной и справочной литературе имеются формулы, выражающие величину 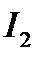непосредственно через коэффициенты дифференциального уравнения замкнутой системы. Оценка 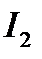является относительной мерой быстродействия САУ: меньшей 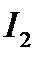соответствует более быстродействующий переходный процесс (рис. 15.10, в).

При минимизации 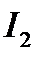и выборе варьируемых параметров обычно получают колебательный переходный процесс с высоким 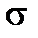% и значительной колебательностью. Например на рис. 15.11 приведены две кривые, удовлетворяющие одному значению 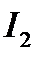: кривая 1 дает некачественный переходный процесс, кривая 2 - переходный процесс, близкий к оптимальному.

x

t

Рис. 15.11 - Процессы с одинаковыми значениями :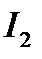

1 - неоптимальный, 2 - близкий к оптимальному

Стремление оценки 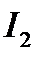к нулю приближает кривую переходного процесса к скачку, так как при этом уменьшается квадратичная площадь, ограниченная кривой. Очевидно, что предельным переходным процессом будет тот, при котором оценка 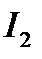стремится к нулю. Это, в свою очередь, вызывает значительное увеличение скорости (рывок скорости) в начальной части процесса. Такой переходный процесс не может быть физически реализован из-за инерционности звеньев САУ и возникающих в системе значительных перегрузок.

Чтобы получить затухающий, но достаточно плавный процесс, вводят улучшенную квадратичную интегральную оценку качества:

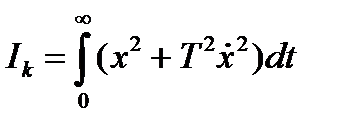. (15.13)

Интегральная оценка 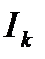состоит из суммы двух частей: первой, соответствующей 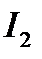, и второй, учитывающей скорость изменения 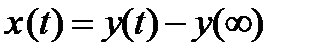с весом 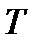(ограничение на скорость изменения 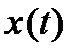). Таким образом, 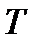назначается в соответствии с заданием желаемых свойств переходного процесса.

Покажем, что при стремлении уменьшить величину 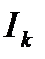, кривая переходного процесса приближается к экспоненте с желаемой постоянной времени 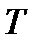. Для этого проделаем следующие преобразования (15.12):

.

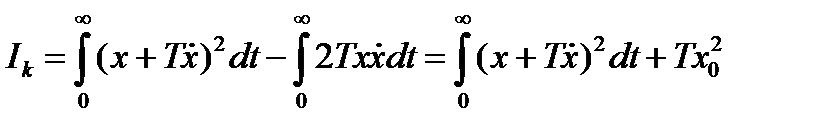Наименьшее возможное значение 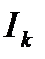будет при 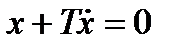. Решение этого дифференциального уравнения 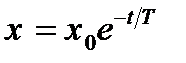является экспонентой, к которой приближается переходный процесс при стремлении уменьшить значение интегральной оценки 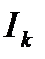. Применяются и другие виды интегральных оценок качества :

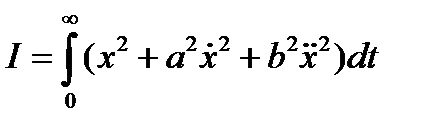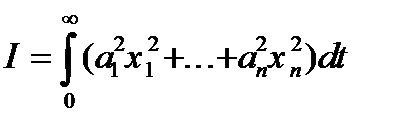; , где 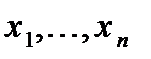- переменные, характеризующие состояние системы.

В общем случае .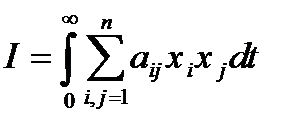

В качестве интегральных критериев используются функционалы и более общего вида. Иногда в выражение интегральной оценки вводится время 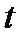в явном виде.

Интегральные оценки в качестве критерия оптимальности широко используются в теории оптимальных САУ.

Линейные и квадратические интегральные функционалы как критерии качества переходного процесса. Методы их вычисления.

Рассмотрим проблему вычисления интеграла линейной интегральной оценки. Можно сначала решить аналитически дифференциальные уравнения, описывающие систему, далее определить ошибку регулирования, затем подставить выражение для ошибки в интеграл линейной оценки и, взяв его, получить выражение для .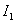

Но можно поступить и иначе.

Пусть свободное движение ошибки регулирования системы описывается уравнением

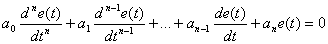(15.14)

Проинтегрируем это уравнение –

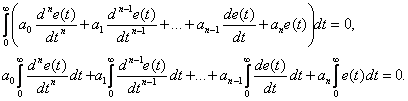
После интегрирования получаем –

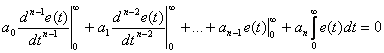	(15.15)

Подстановки верхнего предела дают члены следующего вида –

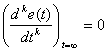	(15.16)

так как все производные ошибки в установившемся режиме обращаются в ноль.

Подстановки нижнего предела дают члены вида –

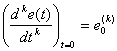	(15.17)

которые являются начальными условиями уравнения (15.14).

Подставив (15.16) и (15.17) в (15.15), получим

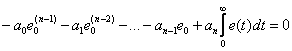(15.18)

А так как

,

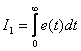окончательно получаем

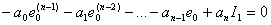(15.19)

Решая (15.19) относительно 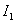, получим выражение для вычисления линейной интегральной ошибки –

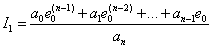	(15.20)

Теперь мы может определить 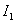по коэффициентам характеристического уравнения системы и начальным условиям переходного процесса ошибки.

Для синтеза систем, определения параметров минимизирующих 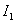, следует воспользоваться обычными методами исследования функций на экстремум. Следовательно, если мы хотим определить параметр системы, на пример, параметр 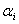, обеспечивающий 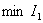, необходимо решить относительно параметра 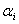следующее уравнение –

.

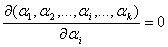Рассмотрим несколько примеров использования линейной интегральной оценки.

Пример

Система имеет характеристическое уравнение

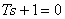(15.21)

Определим выражение для 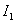, если начальные условия имеют вид –

.

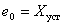Определим значение параметра 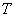, при котором интегральная оценка имеет минимум.

Решение

Обозначим –

.

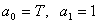Используем для нахождения 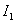выражение (15.20) –

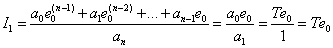(15.22)

Из рассмотрения (15.22) получаем, что 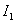в этом случае не имеет экстремума, а меньшее значение интегральной ошибки мы будем получать при меньшем значении 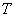. Действительно, ведь уравнение (15.21) является характеристическим уравнением апериодического звена, параметр 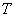– это постоянная времени. Переходный процесс для двух разных постоянных времени будет иметь вид, показанный на рис. 15.12.

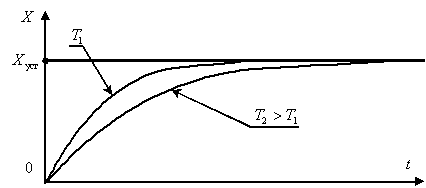
Рис. 15.12

Пример

Система имеет характеристическое уравнение

.

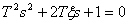Определим выражение для 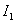, если начальные условия имеют вид –

.

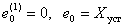Определим значение параметра 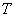, при котором интегральная оценка имеет минимум.

Решение

Обозначим –

.

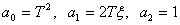Используем для нахождения 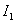выражение (15.20) –

.

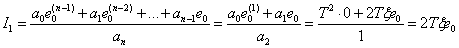Если 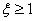, то процессы монотонные, 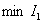обеспечивается при наименьших 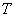и 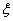. Если 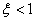, то уменьшение коэффициента затухания уменьшает линейную интегральную оценку, но это приводит к ухудшению переходного процесса, повышению его колебательности.

Интегральные показатели качества представляют собой значения определенных интегралов от тех или иных функций переходной составляющей ошибки eп(t). Наиболее простыми и широко распространенными интегральными оценками являются:

- интегральная квадратичная оценка (ИКО)

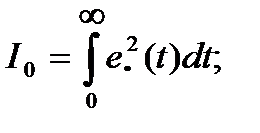(15.23)

- улучшенная ИКО

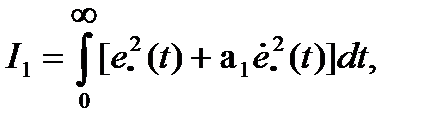(15.24)

где a1 - весовой коэффициент, учитывающий производную ошибки.

ИКО переходного процесса можно вычислить по изображению ошибки

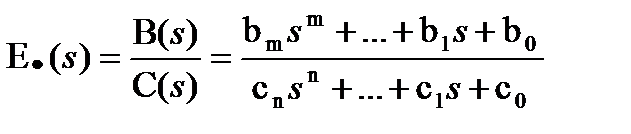(15.25)

с помощью следующих выражений (для m = n-1):

n = 1, 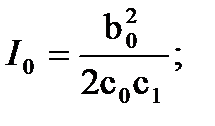(15.26)

n = 2, 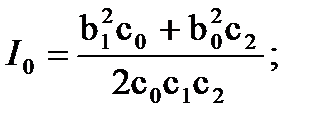(15.27)

n = 3, 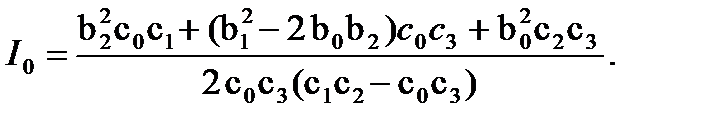(15.28)

Для вычисления улучшенной ИКО выражение (13.13) записывается в виде:

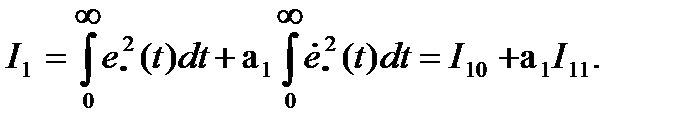(15.29)

Первый интеграл I10 (ИКО ошибки) вычисляется по формулам (15.26), (15.27) или (15.28). Для вычисления второго интеграла (I11) необходимо получить изображение производной ошибки

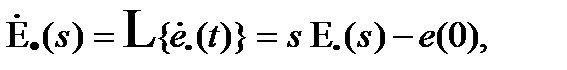(15.30)

где Eп(s) определяется выражением (15.25), а начальное значение ошибки e(0) - по теореме о предельном переходе:

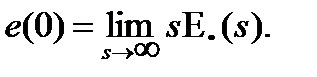(15.31)

Подставив (15.31) в (15.30), получим выражение для изображения производной ошибки

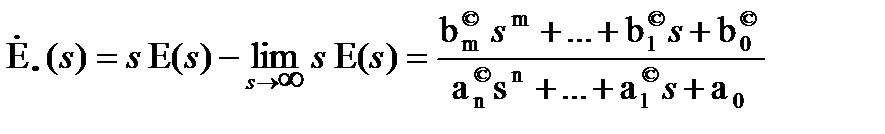, (15.32)

по коэффициентам которого с использованием формул (15.26), (15.27) или (15.28) можно вычислить интеграл I11 в выражении (15.29).

Изображение по Лапласу сигнала на выходе системы имеет вид –

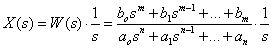(15.33)

где 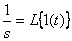- изображение по Лапласу единичной ступенчатой функции – входного сигнала системы.

Для системы автоматического управления, математическая модель которой приведена к виду (15.33), интегральная квадратичная ошибка определяется по следующему выражению –

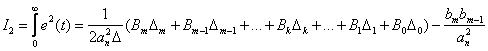(15.34)

где

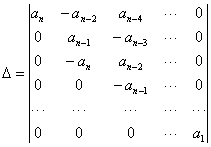(15.35)

в все элементы с индексами меньше 0 и больше 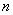заменяются 0.

Определители 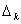в (15.34), где 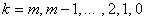, получаются заменой в определителе (15.35) ( 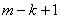)-го столбца столбцом следующего вида –

.

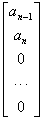Коэффициенты 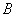в выражении (15.34) определяются следующим образом –

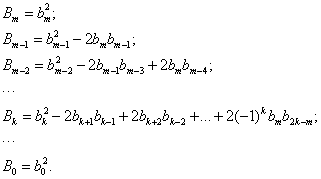(15.36)

при определении 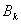коэффициенты, индексы которых меньше 0 и больше 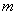, заменяются 0.

Кроме того, часто оказывается, что выбранные по 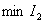параметры системы приводят к существенно колебательному процессу, большим производным из-за стремления приблизить процесс к идеальному скачку.

Поэтому используют еще один вид интегрально квадратичной оценки, в которой ограничение накладывается не только на величину отклонения 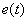, но и на скорость его изменения 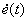. Эта оценка имеет следующий вид –

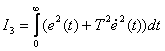(13.26)

где 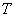– некоторая постоянная времени.

Разницу между оценкам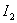и и 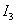можно представить графически, как это показано на рис. 15.13

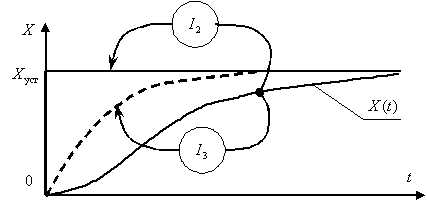
Рис. 15.13

То есть оптимизированный по 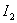переходный процесс стремиться к идеальному скачку, а оптимизированный по 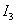– к кривой экспоненциального вида, которая описывается следующим выражением –

.

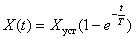Докажем последнее утверждение. Для этого проанализируем выражение (13.26).

,

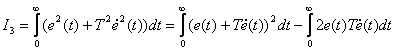с учетом того, что

,

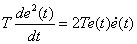получаем

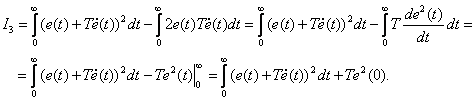(15.38)

С учетом того, что последнее слагаемое в (15.38) является величиной постоянной –

,

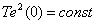квадратичная оценка 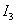будет иметь минимум при

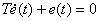(15.39)

Решение дифференциального уравнения (15.39) имеет вид –

,

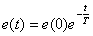а если перейти от ошибок к выходным переменным, то получим –

,

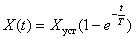что и требовалось доказать.

Следовательно, выбирая параметры системы по 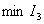, можно приблизить переходный процесс к экспоненте с заданной постоянной времени 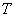, тем самым вводится ограничение на скорость нарастания выходной величины .

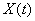Методика определения 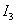может быть аналогичной методике определения 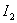, рассмотренной выше, если представить квадратичную оценку с учетом производной в следующем виде –

,

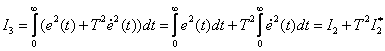где 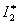определяется по формулам для 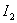, но с учетом того, что порядок числителя 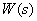– 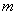увеличивается на 1.

В теории автоматического управления используют квадратичные оценки с производными более высокого порядка (до 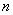) для более точного задания желаемой формы переходного процесса, естественно, что при этом усложняется и процесс вычисления оценок.

Вычисление квадратичных интегральных оценок

Рассмотрим вычисление и использование квадратичных ошибок на примере.

Пример

В системе управления с передаточной функцией –

,

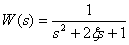зададим :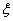

· из условия ,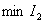

· из условия ,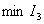

и сравним переходные процессы для двух этих случаев.

Решение

Получим выражение для 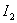. Для этого преобразуем передаточную функцию системы к заданному виду

,

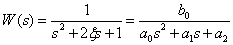тогда получим

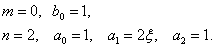(15.40)

Выражение для 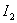принимает вид –

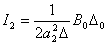(15.41)

Определим компоненты (15.41) попараметра передаточной функции системы (15.40).

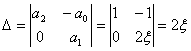(15.42)

Для нахождения 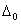определим ( 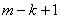), при ,

,

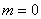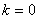
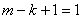Заменим в выражении (15.42) для первый столбец столбцом вида

.

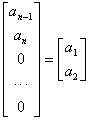Тогда получаем

.

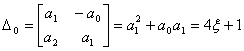Определим –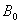

.

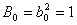После подстановки полученных компонент в (15.41) получаем выражение для квадратичной интегральной оценки.

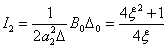(15.43)

Найдем выражение для частной производной по 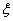от выражения (15.43)

,

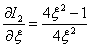приравнивая полученное выражение к нулю получаем уравнение для нахождения оптимального значения .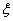

.

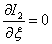В результате получаем оптимизированное по квадратичной оценке значение –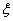

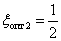(14.44)

Передаточная функция системы при 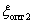примет вид –

.

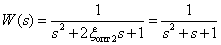На рис. 15.14 покажем вид переходного процесса системы при единичном ступенчатом воздействии и оптимизированным по 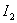параметром.

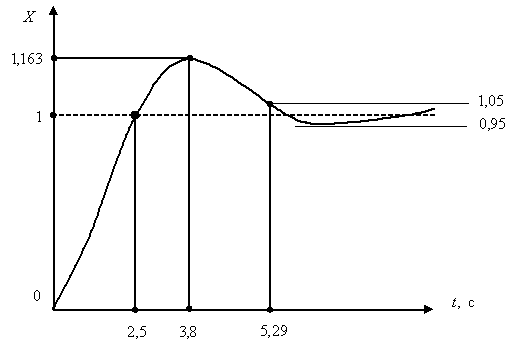
Рис. 15.14

Таким образом, имеем следующие показатели качества переходного процесса,

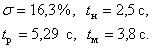(15.45)

Определим 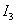по отработанной выше методике для –

,

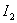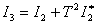выражение для 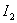берем из предыдущего случая –

.

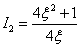Определим теперь 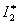. Передаточная функция системы для этого случая имеет вид –

,

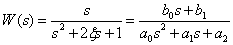тогда получим

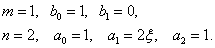(15.46)

Выражение для 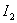принимает вид –

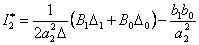(15.47)

Определим компоненты (15.47) по параметрам передаточной функции системы (15.46).

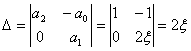(15.48)

Определим коэффициенты –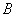

.

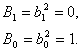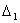не определяем, так как 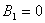. Для нахождения 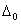определим ( 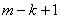), при ,

,

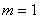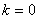
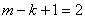Заменим в выражении (10) для второй столбец столбцом вида

.

Тогда получаем

.

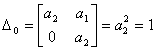После подстановки полученных компонент в (15.47) получаем выражение для квадратичной интегральной оценки.

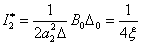(15.49)

Окончательно получаем

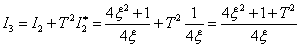(15.50)

Найдем выражение для частной производной по 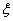от выражения (15.50)

,

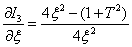приравнивая полученное выражение к нулю получаем уравнение для нахождения оптимального значения .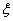

.

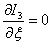В результате получаем оптимизированное по квадратичной оценке с учетом производной значение –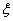

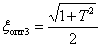(15.51)

Полагаем для определенности 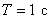, тогда

.

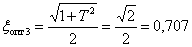Передаточная функция системы при 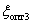примет вид –

.

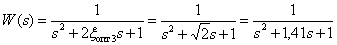На рис. 15.15. покажем вид переходного процесса системы при единичном ступенчатом воздействии и оптимизированным по 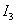параметром.

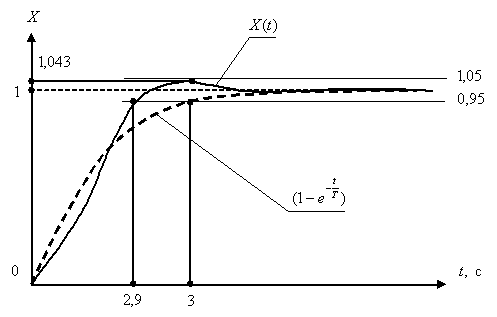
Рис. 15.15

Таким образом, имеем следующие показатели качества переходного процесса,

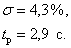(15.52)

Сравнивая переходные процессы, видим, что при оптимизации по квадратичной оценке с учетом производной ( 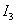) получили существенно меньшие значения перерегулирования и быстродействия, при более плавном нарастании переменной.

Интегральные показатели качества регулирования дают совокупную оценку быстродействия и колебательности без вычисления их значений. Они характеризуют отклонение реального переходного процесса от заданного идеального.

Интегральная линейная оценка (ИЛО) определяется площадью отклонения реального процесса от идеального ступенчатого. Для обеспечения требуемых динамических свойств САУ необходимо выразить величину J1 через коэффициенты передаточной функции системы

,

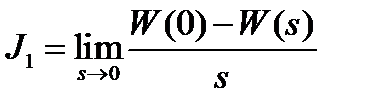где W(0) – значение передаточной функции в установившемся режиме (при s = 0), а затем найти оптимальные значения варьируемых параметров, соответствующих минимуму J1.

Пример 1. Для системы с передаточной функцией

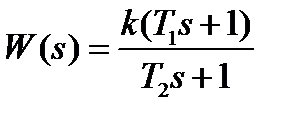
линейная интегральная оценка

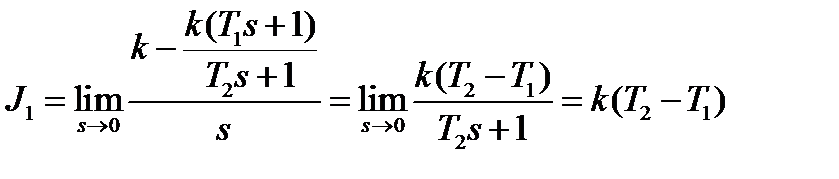
зависит от соотношения постоянных времени Т₁ и Т₂. Минимум оценки достигается при их равенстве.

Задания №15.1Прямые оценки качества регулирования

15.1.1 Оценить качество регулирования для звена с передаточной функцией .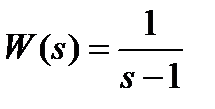

15.1.2 Сформулировать условия отсутствия перерегулирования в системе с дифференциальным уравнением .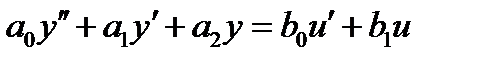

15.1.3 Определить величину перерегулирования системы (рисунок 115.16) от скачка задания

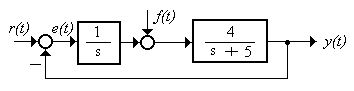
Рисунок 15.16

15.1.4 Найти все показатели качества регулирования (рисунок 15.17)

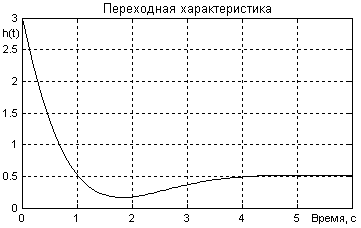
Рисунок 15.17

15.1.5 Оценить основные показатели качества регулирования (рисунок 15.18) относительно возмущения

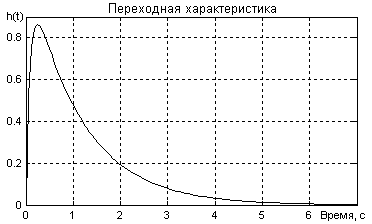
Рисунок 15.18

15.1.6 Найти время регулирования t_рег, степень демпфирования и величину перерегулирования σ по переходной характеристике выхода системы относительно возмущения (рисунок 15.19)

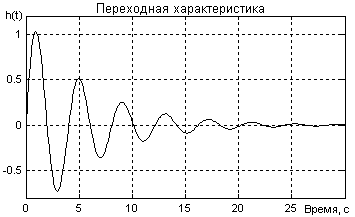
Рисунок 15.19

Задания № 15.2 Корневые методы оценки качества регулирования

15.2.1 Оценить степень устойчивости и степень колебательности системы с D(s) = (s + 1)(s² + 2s+ 2).

15.2.2 Найти показатели качества системы с характеристическим уравнением D(s) = s³ + s² + 2s + 3 = 0.

15 2.3 Оценить степень устойчивости и степень колебательности системы (рисунок 15.20)

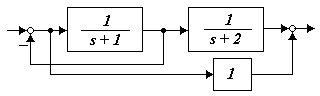
Рисунок 15.20

15.2.4 Найти время регулирования системы (рисунок 15.21)

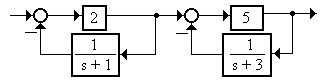
Рисунок 15.21

15.2.5 Найти t_рег и σ системы (рисунок 15.22), если k = 3

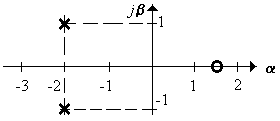
Рисунок 15.22

15.2.6 Рассчитать перерегулирование и время регулирования для системы (рисунок 15.23)

Рисунок 15.23

15.2.7 Оценить приблизительно t_рег и σ системы (рисунок 15.24) для произвольного значения k

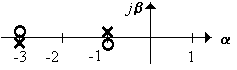
Рисунок 15.24

Задания№ 15.3 Частотные методы оценки качества регулирования

1 Оценить t_рег и σ системы с ПФ W(s) = 4/(s² + 6s +8), используя частотный метод.

2 Найти оценки показателей качества по ВЧХ (рисунок 15.25), считая ω₊ = ω_сущ

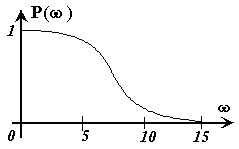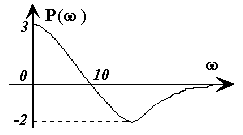Рисунок 15.25	Рисунок 15.26

3 Найти по вещественной частотной характеристике P(w) показатели качества переходного процесса s, t_рег (рисунок 15.26)

4 Найти частотным методом показатели качества s и t_рег после замыкания системы, если передаточная функция разомкнутой системы равна W(s) = 9/(s² +11s + 1).

5 Оценить частотным методом установившуюся ошибку системы с передаточной функцией W(s) = 9/(s³ +2s² +6s + 10).

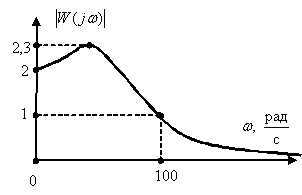
6.По графику АЧХ системы определить показатель колебательности и частоту среза системы.

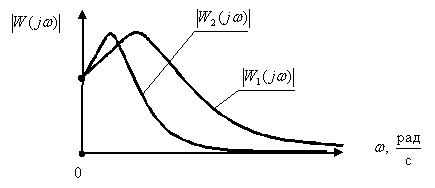
7 По графикам АЧХ двух систем: САУ1 – 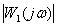, САУ2 – 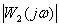, определить систему управления, переходные процессы которой имеют большую колебательность.

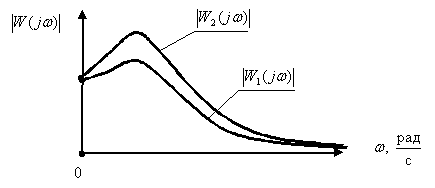
8.По графикам АЧХ двух систем: САУ1 – 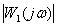, САУ2 – 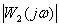, определить систему управления, которая имеет большее быстродействие.

9. С помощью частотного метода по ВЧХ и АЧХ определить показатель колебательности, приближенное время переходного процесса и полосу пропускания для линейной системы автоматического управления со следующей структурной схемой

11 С помощью частотного метода по АЧХ определить показатель колебательности, приближенное время переходного процесса и полосу пропускания для линейной системы автоматического управления со следующей структурной схемой

11 С помощью частотного метода определить по ВЧХ и АЧХ показатель колебательности, приближенное время переходного процесса и полосу пропускания для линейной системы автоматического управления со следующей структурной схемой

12. С помощью частотного метода определить показатель колебательности, приближенное время переходного процесса и полосу пропускания для линейной системы автоматического управления со следующей структурной схемой

13 .С помощью прямого и косвенного метода определить оценки качества регулирования для линейных системы автоматического управления со структурными схемами, приведенными ниже

а)

вариант	K	Т,с	
		0,1с	0,3
		0,3	0,05
		0,5	0,5
		0,7	0,4
		0,9	0,8
			0,04
		0,8

б)

вариант	K	Т,с	ξ
		0,1с	0,3
		0,3	0,05
		0,5	0,5
		0,7	0,4
		0,9	0,8
			0,04
		0,8

в)