Второй закон термодинамики

3.1. Формулировки и математическое выражение
второго закона термодинамики

Формулировка Клаузиуса. Теплота не может сама собой переходить от холодного тела к горячему.

Формулировка Больцмана. Все естественные процессы являются переходом от менее вероятного состояния к более вероятному.

Формулировка Карно. Для превращения теплоты в работу необходимо иметь два источника теплоты разной температуры (рис. 3.1).

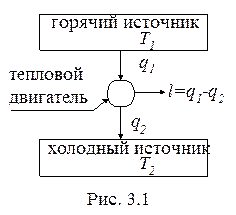Горячим источником в тепловых двигателях является топливо (органическое или ядерное), солнечная энергия, геотермальная энергия и т.д., холодным источником – окружающая среда.

Здесь q₁ – теплота, подводимая от горячего источника к рабочему телу в тепловом двигателе; q₂ – отводимая теплота от рабочего тела; l – работа, полученная в тепловом двигателе.

Одна из формулировок второго закона термодинамики гласит: вечный двигатель второго рода невозможен. Это двигатель, который бы работал без холодного источника и всю подводимую теплоту (q₁) преобразовывал в работу.

Таким образом, работа полностью превращается в теплоту, в то время как теплота превращается в работу – только частично.

Математическое выражение второго закона термодинамики для обратимых процессов имеет вид:

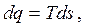	(3.1)
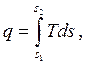	(3.2)

где q - подводимая (извне) или отводимая от рабочего тела теплота;

s, Дж/(кг^.К)– удельная энтропия, являющаяся параметром состояния

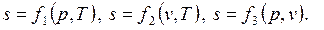На основании (3.1) можно сделать следующие выводы:

1. При подводе тепла к рабочему телу (dq > 0) энтропия возрастает
(ds > 0).

2. При отводе тепла от рабочего тела (dq < 0) энтропия убывает (ds < 0).

3. В адиабатных процессах и системах (dq = 0) энтропия не изменяется (ds = 0, s = const).

4. В изотермических процессах выполняется равенство

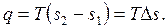Математическое выражение второго закона термодинамики для необратимых процессов

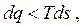	(3.3)
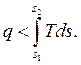	(3.4)

Трение и неравновесность реальных процессов сжатия и расширения относят к внутренней необратимости. Необратимый теплообмен между телами при конечной разности температур называется внешней необратимостью.

Как внутренняя, так и внешняя необратимости сопровождаются увеличением энтропии (Ds_H), что и учитывается уравнениями (3.3) и (3.4).

3.2. T-s-диаграмма

На рис. 3.2 в T-s- диаграмме показан произвольный процесс 1-2.

Согласно уравнениям (3.1) и (3.2) площадь под кривой (s₁-1-2-s₂) характеризует теплоту этого процесса.

Теплота подводится (dq > 0), если энтропия увеличивается (ds > 0, s₂ > s₁). Теплота отводится (dq < 0), если энтропия уменьшается (ds < 0, s₂ < s₁). Теплота (q), как и работа (w, l), является функцией процесса, зависит от его характера.