Функция распределения Пуассона
Функцияраспределения Пуассона задает вероятность прихода n заявок в интервале длительностью t в соответствии с выражением:
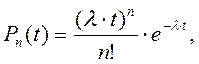
 где n ³ 0;
где n ³ 0;
λt – число заявок за время t, носит название параметра распределения.
На рис. 5.8 показаны кривые распределения Пуассона для разных значений n.
С математической точки зрения распределение Пуассона является дискретным многомерным распределением вероятностей.
Из рисунка 5.8 видно, что с увеличением интервала времени вероятность отсутствия заявки (n=0) только уменьшается, тогда как графики вероятностей прихода 1, 2, 3 и т.д. заявок (соответственно n =1,2,3 и т.д.) имеют максимумы. Это объясняется тем, что с увеличением временного интервала вначале вероятность поступления именно данного числа заявок возрастает, а затем начинает уменьшаться – за счет возрастания вероятности прихода большего (чем данное n) числа заявок.
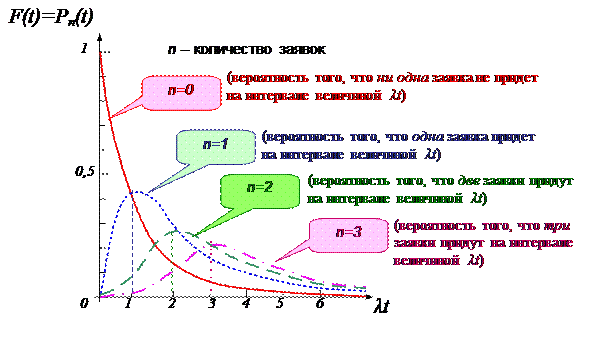
Рис. 5.8. Функция распределения простейшего пуассоновского потока заявок
5.1.7. Характеристики обслуживания
1. Функция распределения времени обслуживания (интервала занятости) F*(t)
Характеризует процесс обслуживания заявок, поступающих в СМО. Задается конкретным выражением закона распределения, например, любого из приведенных в Приложении 3.
2. Плотность распределения времени обслуживания w*(t)
Эта характеристика (аналогично вышеупомянутой плотности из п.3) представляет собой производную по времени от функции распределения вероятности F*(t):
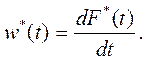
 |
3. Среднее время обслуживания (интервала занятости):
Усредненная характеристика процесса обслуживания (аналогичная вышеупомянутому математическому ожиданию из п. 4).

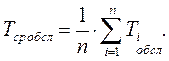
Показательный закон распределения времени обслуживания
Часто используется показательный закон распределения времени обслуживания (рис. 5.9).
Функция распределенияв этом случае имеет вид:
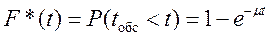
Плотность распределения:
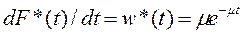

Рис. 5.9. Функция распределения и плотность распределения времени обслуживания для показательного закона
Среднее время обслуживания равно:
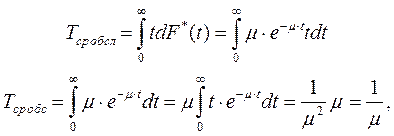
где μ – средняя скорость обслуживания;
μt – число заявок за время обслуживания t.
Д о с т о и н с т в а и с п о л ь з о в а н и я э к с п о н е н ц и а л ь н о г о
з а к о н а р а с п р е д е л е н и я
1) Вероятность, что время обслуживания закончится в малом интервале dt, не зависит от длительности предыдущего интервала обслуживания (система без памяти).
2) При прерывании обслуживания через время Т, оставшееся время (t–T) также распределено по экспоненциальному закону с тем же параметром μ.
